Наивный подход

Казалось бы, оценить параметры можно из элементарного здравого смысла. Оценку наклона 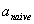прямой регрессии получим, поделив приращение 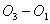при переходе от x₁ =-1 к x₃=+1 на , а оценку значения найдем как среднее арифметическое:

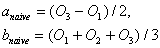
Легко проверить, что математические ожидания оценок равны (оценки несмещенные).

После того как оценки получены, H₀ проверяют как обычно с помощью хи-квадрат критерия Пирсона:

Оценки ожидаемых частот можно получить, исходя из оценок :

При этом, если наши оценки ”правильные”, то расстояние Пирсона будет распределено как случайная величина хи-квадрат с одной степенью свободы: 3-2=1. Напомним, что мы оцениваем два параметра, подгоняя данные под нашу модель. При этом сумма не фиксирована, поэтому дополнительную единицу вычитать не нужно.

Однако, подставив , получим странный результат:

С одной стороны, ясно, что для данных частот нет оснований отвергать H₀, но мы не в состоянии это проверить с помощью хи-квадрат критерия, так как оценка ожидаемой частоты в первой точке оказывается отрицательной. Итак, найденные из “здравого смысла” оценки не позволяют решить задачу в общем случае.