Занятие №47. Геометрический смысл производной

Геометрический смысл производной: Тангенс угла наклона касательной проведённой к точке графика функции равен значению производной этой функции в точке . Т.е. .

Т.к. , окончательно получаем: .

После подстановки значений данное уравнение можно привести к виду: .

Прим.1: найти тангенс угла наклона касательной в точке к графику функции .

Найдём производную функции: ;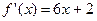

Найдём значение производной в точке : ;

.

Прим.2: найти угол наклона касательной проведённой к точке графика функции .

Найдём производную функции: ;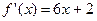

Найдём значение производной в точке : ;

Прим.3: найти абсциссу точки в которой касательная к графику функции находится под углом 45 градусов к положительному направлению оси Ох.

.

Прим.4: найти точки в которых касательная к графику функции параллельна оси Ох.

.

1. Найти тангенс угла наклона касательной в точке к графику функции:

1) ; 2) ; 3) ; 4) ;

2. Найти тангенс угла наклона касательной в точке :

1) ; 2) ; 3) ; 4) ;

3. Найти тангенс угла наклона касательной в точке :

1) ; 2) ; 3) ; 4) ;