 |
Главная Случайная страница Контакты | Мы поможем в написании вашей работы! | |
Процесс ортогонализации
|
|
Опр: ВП V над R с введённым на нем скалярным произведением называется евклидовым пространством.
Пример1: На Rn введём скалярное произведение так:
`a=(a1,a2,…,an),`b=(b1,b2,…,bn).
Назовем скалярным произведением (`a,`b)=a1b1+a2b2+…+anbn
Пример2: V3- геометрическое векторное пространство радиус-векторов плоскости.
Опр: Пусть Е – евклидово пространство. а, bÎЕ, а и b называются ортогональными, если (а,b)=0.
Опр: Система векторов пространства Е называется о ртогональной, если все векторы этой системы попарно ортогональны.
Теорема: Ортогональная система векторов линейно независима (обратное не выполняется).
Опр: Базис называется ортогональным, если все его векторы попарно ортогональны.
Опр: Вектор наз. нормированным (единичным), е/и его скалярный квадрат =1.
Опр Базис наз. ортонормированным, если все векторы в нём попарно ортогональны и каждый вектор ортонормирован.
Процесс ортогонализации.
Зададимся целью из произвольного базиса ВП построить ортонормированный. Разобьём задачу:
1.Из произвольного базиса построим ортогональный.
2.Нормируем полученный базис.
Рассмотрим произвольный базис (a1,a2,…,an) евклидова ВП. Построим ортогональный базис e1,e2,…,en.
1) b1=a1
2) b2=l1b1+a2. l1 найдём из условия ортогональности векторов
(b1,b2)=0;(b1,l1b1+a2)=0Þl1=-(b1,a2)/(b1,b1). Подставив l1 в b2 найдем вектор b2.
3.b3=m1b1+m2b2+a3;
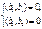
(m1b1+m2b2+a3,b1)=0; Þm2=-(a3,b)/(b1,b1).
Этот процесс конечен, состоит из n шагов, он позволяет получить ортогональный базис, который можно нормировать.
Опр.: Ортонормированным базисом Евклидова простр-ва Е наз-ся ортогональный базис этого простр-ва, каждый вектор которого нормирован.
Теор: Всякое n-мерное Евклидово простр-во обладает ортонормир-м базисом. (Простр-во Е обладает ортогональным базисом {a1,a2,…,an}. Нормируя каждый из векторов базиса получим ортонормируемый базис {e1,e2,…,en}).
(к билету №10) Найти 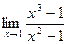
Решение:
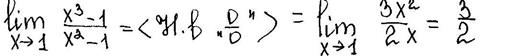
Дата публикования: 2015-07-22; Прочитано: 181 | Нарушение авторского права страницы | Мы поможем в написании вашей работы!
