Построение формул алгебры логики по заданной таблице истинности

Пусть F – двоичная функция от n переменных. Предположим, что F не равна тождественно нулю. Пусть T₁, T₂, …, T_k – все точки ее определения, в которых F =1. Можно доказать, что справедлива следующая формула:

,

где , j=1,2,…, k,

Построить функцию F можно и по-другому. Если функция F не равна тождественно единице и S₁, S₂,…, S_m – все точки области ее определения, в которых F =0, то справедлива формула:

,

где , j=1,2,…, m.

Из приведенных формул видно, что любую двоичную функцию можно записать, используя лишь операции, , .

Основная конъюнкция – это конъюнкция основных высказываний переменных или их отрицаний. Например, .

Основная дизъюнкция – это дизъюнкция основных высказываний переменных или их отрицаний. Например, .

Конъюнктивной нормальной формой (КНФ) данной формулы называется формула, равносильная данной и представленная в виде конъюнкции основных дизъюнкций. Например, (A+B) (A+C+B) (D+A).

Дизъюнктивной нормальной формой (ДНФ) данной формулы называется формула, равносильная данной и представленная в виде дизъюнкции основных конъюнкций. Например, AB+C+AC.

Теорема 1. Для того чтобы формула алгебры высказываний была тождественно истинной, необходимо и достаточно, чтобы ее КНФ содержала в каждой элементарной дизъюнкции некоторое высказывание и его отрицание.

Теорема 2. Для того чтобы формула алгебры высказываний была тождественно ложной, необходимо и достаточно, чтобы ее ДНФ содержала в каждой элементарной конъюнкции некоторое высказывание и его отрицание.

Совершенные дизъюнктивные, конъюнктивные и полиномиальные нормальные формы представления переключательных (логических) функций. Многообразие формул, посредством которых может быть выражена любая логическая функция, определяет многообразие форм логических функций, т. е. способов их записи путем применения к переменным и их группам элементарных логических операций. Наиболее удобными для практического использования оказываются совершенные нормальные формы представления сложных логических функций. В алгебре логики доказывают, что любая логическая функция F (A, B, C,…, N) может быть представлена только одной совершенной дизъюнктивной нормальной формой (кроме константы нуль) или только одной совершенной конъюнктивной нормальной формой (кроме константы единица).

Пусть функция X=F (A, B, C) задана таблицей 4. Запись функции Х в виде логической суммы (дизъюнкции) логических произведений (конъюнкций) переменных, для которых значение функции Х равно 1, и является совершенной дизъюнктивной нормальной формой (СДНФ) представления логической функции.

Таблица 4

A	B	C	X

СДНФ логической функции следует находить в такой последовательности:

1) составить произведения переменных для строк таблицы истинности, в которых Х равна 1. Если значение переменной (А, В или С) в строке равно 0, то в произведении записывается отрицание этой переменной;

2) написать сумму произведений, для которых функция Х равна 1. Полученная сумма и является СДНФ. В общем виде

, (1)

Это правило называют правилом записи переключательной функции по единицам. Согласно этому правилу, данные табл. 4 описываются аналитическим выражением, связывающим все наборы переменных, для которых Х =1, в виде:

. (2)

Запись функции Х в виде логического произведения (конъюнкции) логических сумм (дизъюнкций) переменных, для которых функция Х равна 0, является совершенной конъюнктивной нормальной формой (СКНФ) представления логической функции.

Для табл. 4 аналитическое выражение в СДНФ, связывающее все наборы переменных, для которых Х =0, имеет вид:

. (3)

Для представления логической функции Х в СКНФ произведем операцию отрицания левой и правой частей равенства (3)

и на основании законов двойного отрицания и инверсии

. (4)

СКНФ логической функции, согласно (4), следует находить в такой последовательности:

1) составить логические суммы переменных для строк таблицы истинности, в которых функция Х равна 0. Если значение переменной (А, В или С) в строке равно 1, то в сумме записывается отрицание этой переменной;

2) написать логическое произведение составленных логических сумм. Полученное произведение и является СКНФ. В общем виде:

, (5)

где F_i – сложные дизъюнкции.

Это правило также называют правилом построения переключательной функции по нулям.

Кроме представления функций в виде СДНФ и СКНФ используют и совершенную полиномиальную нормальную форму СПНФ. Вместо дизъюнкции может быть записана функция сложения по модулю два (сумма Жегалкина):

, (6)

где F_i – сложные конъюнкции.

Существует специальная таблица, в которой все элементарные логические операции от двух аргументов представлены в двух совершенных нормальных формах.

Нормальные формы представления переключательной функции иногда называют стандартными (табл. 5).

Таблица 5

f	A B	Название функции	Обозначение функции	СДНФ	СКНФ
f0		Константа нуль		Не имеет
f1		Логическое произведение, конъюнкция
f2		Функция запрета по В
f3		Переменная А
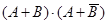
f4		Функция запрета по А
f5		Переменная В
f6		Сумма по мо дулю 2, логическая неравнозначность
f7		Логическое сложение, дизъюнкция
f8		Операция (стрелка) Пирса, операция Вебба
f9		Эквивалентность, логическая равнозначность
f10		Инверсия В
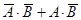
f11		Импликация от В к А
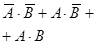
f12		Инверсия А
f13		Импликация от А к В
f14		Операция (штрих) Шеффера
f15		Константа единица			Не имеет

Многочленом Жегалкина называется многочлен, являющийся суммой константы 0 или 1 и различных одночленов, в которые все переменные входят не выше, чем в первой степени.

Теорема. Любая функция булевой алгебры может быть представлена, и притом единственным образом, с помощью полинома Жегалкина вида

J = .

Представим, например, в виде полинома выражение вида X₁ X₂. Для этого проведем следующие рассуждения.

Пусть

X₁ X₂ = aX₁X₂+bX₁+cX₂+k,

где а, b, с, k – неопределенные коэффициенты.

При X₁ = X₂ = 0 имеем k = 0. При Х₁ = 1, X₂ = 0 имеем b = 1. При Х₁ = 0, Х₂ = 1 имеем с = 1. При X₁=Х₂ = 1 имеем а + b + с = 1, т. е. а = -1. Таким образом, получаем:

X₁ X₂ = – X₁X₂+ X₁+ X₂.

СПНФ образуется путем замены в СДНФ: на + и на

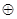1 х.

,

,

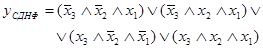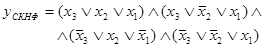В последнем случае выражение для легко можно упростить, если раскрыть скобки и взаимно сократить все одинаковые слагаемые, входящие в формулу четное число раз:

.

Подобное упрощение, которое называется минимизацией логической функции, можно осуществить и по отношению к СДНФ и СКНФ.

Таблица 6

			y

Применение законов алгебры логики позволяет найти более компактные аналитические выражения для заданной функции у, т. е. минимальную дизъюнктивную нормальную форму . Приведем соответствующие формы представления функции у, заданной табл. 6:

,

и для СКНФ, т. е. минимальную КНФ:

.

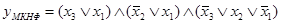После того, как найдены минимальные нормальные формы (МНФ), их рекомендуется проверить на всех наборах аргументов . Переменные или часто называют термами. Именно полный набор из n термов образует конституенту. В процессе же минимизации некоторые термы из конституент пропадут. Тогда оставшуюся часть дизъюнкта или конъюнкта называют импликантой.

Как мы только что убедились на примере, импликанты появляются в результате склейки смежных конституент, различающихся одним термом.

Контрольные вопросы и упражнения

1. Дайте определение логической функции многих переменных.

2. Что такое вектор значений булевой функции? Приведите пример построения таблицы истинности логической функции многих переменных.

3. Сколько существует булевых функций от n переменных?

4. Что такое ДНФ и КНФ?

5. Каков алгоритм построения СДНФ? Приведите пример построения СДНФ.

6. Каков алгоритм построения СКНФ? Приведите пример построения СКНФ.

7. Составьте СКНФ и СДНФ для функции .

8. Приведите пример построения СПНФ.