Модель М/М/1

Существует ветвь прикладной математики, предметом которой являются процессы образования очередей. Эта дисциплина так и называется — теория очередей. Мы не будем углубляться в математические основы этой теории, приведем только некоторые ее выводы, существенные для рассматриваемой нами проблемы QoS.

На рис. 7.3 показана наиболее простая модель очереди, известная под названием М/М/1[26].

Рис. 7.3. Модель М/М/1

Основными элементами модели являются:

□ входной поток абстрактных заявок на обслуживание;

□ буфер;

□ обслуживающее устройство;

□ выходной поток обслуженных заявок.

Заявки поступают на вход буфера в случайные моменты времени. Если в момент поступления заявки буфер пуст и обслуживающее устройство свободно, то заявка сразу же передается в это устройство для обслуживания. Обслуживание также длиться случайное время.

Если в момент поступления заявки буфер пуст, но обслуживающее устройство занято обслуживанием ранее поступившей заявки, то заявка ожидает его завершения в буфере. Как только обслуживающее устройство завершает обслуживание очередной заявки, она передается на выход, а прибор выбирает из буфера следующую заявку (если буфер не пуст). Выходящие из обслуживающего устройства заявки образуют выходной поток. Буфер считается бесконечным, то есть заявки никогда не теряются из-за того, что исчерпана емкость буфера.

Если прибывшая заявка застает буфер не пустым, то она становится в очередь и ожидает обслуживания. Заявки выбираются из очереди в порядке поступления, то есть соблюдается дисциплина обслуживания первым пришел — первым обслужен (First-In, First-Out, FIFO).

Теория очередей позволяет оценить для этой модели среднюю длину очереди и среднее время ожидания заявки в очереди в зависимости от характеристик входного потока и времени обслуживания.

Будем считать, что среднее время между поступлениями заявок известно и равно Т. Это значит, что интенсивность поступления заявок, которая традиционно обозначается в тео­рии очередей символом 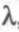, равна 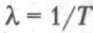заявок в секунду.

Случайный процесс поступления заявок описывается в этой модели функцией распределения интервалов между поступлениями заявок. Чтобы упростить получение компактных аналитических результатов, обычно считают, что эти интервалы описываются так называемым марковским распределением (другое название — пуассоновское), плотность которого показана на рис. 7.4. Из рисунка видно, что входной поток является существенно пульсирующим, так как есть ненулевая вероятность того, что интервал между заявками будет очень небольшим, близким к нулю, а также того, что он будет очень большим. Среднее отклонение интервалов также равно Т.

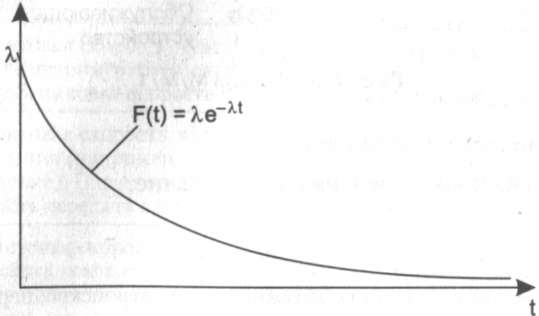
Рис. 7.4. Плотность распределения входного потока

Будем также считать, что среднее время обслуживания заявки равно b. Это означает, что обслуживающий прибор способен продвигать заявки на выход с интенсивностью 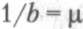. Опять же для получения аналитического результата считают, что время обслуживания — это случайная величина с пуассоновской плотностью распределения.

Принятие таких предположений дает простой результат для среднего времени ожидания заявки в очереди, которое мы обозначим через :

Здесь через 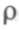обозначено отношение

Параметр 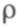называют коэффициентом использования (utilization) обслуживающего прибора. Для любого периода времени этот показатель равен отношению времени занятости обслуживающего прибора к величине этого периода.

Зависимость среднего времени ожидания заявки от иллюстрирует рис. 7.5. Как видно из поведения кривой, параметр играет ключевую роль в образовании очереди. Если значение близко к нулю, то среднее время ожидания тоже очень близко к нулю. А это означает, что заявки почти никогда не ожидают обслуживания в буфере (в момент их прихода он оказывается пустым), а сразу попадают в обслуживающее устройство. И наоборот, если 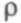приближается к 1, то время ожидания растет очень быстро и нелинейно (и в пределе равно бесконечности). Такое поведение очереди интуитивно понятно, ведь 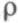— это отношение средней интенсивности входного потока к средней интенсивности его обслуживания. Чем ближе средние значения интервалов между пакетами к среднему времени обслуживания, тем сложнее обслуживающему устройству справляться с нагрузкой.

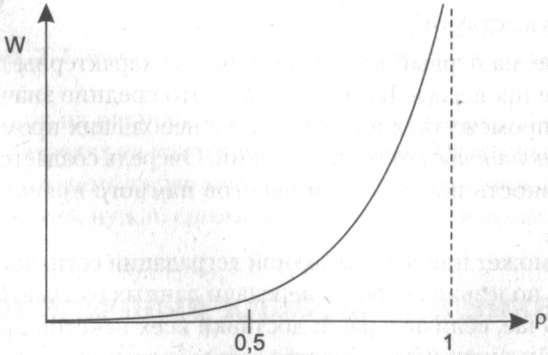
Рис. 7.5. Зависимость среднего времени ожидания заявки от коэффициента использования ресурса

С помощью модели М/М/1 можно приближенно моделировать сеть с коммутацией пакетов (рис. 7.6).

Так, входной поток пакетов, поступающих на вход интерфейса коммутатора (будем здесь использовать этот термин как обобщенное название устройства коммутации пакетов), представлен в модели потоком заявок, а буфер модели соответствует буферу интерфейса коммутатора. Среднее время обслуживания заявки соответствует среднему времени продвижения пакета процессором коммутатора из входного буфера в выходной канал.

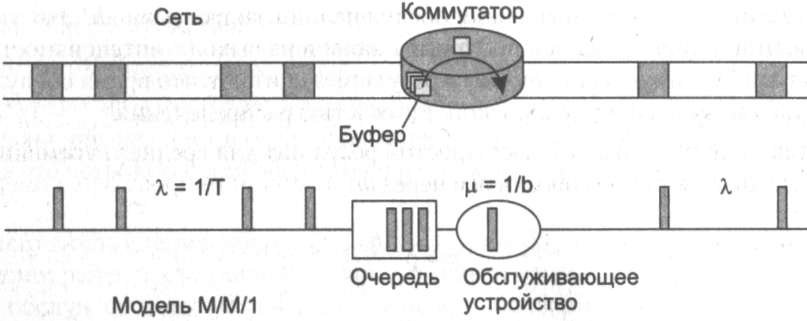
Рис. 7.6. Выходной интерфейс как разделяемый ресурс коммутатора

Понятно, что приведенная модель очень упрощенно описывает процессы, происходящие в коммутаторе. Тем не менее, она очень полезна для понимания основных факторов, влияющих на величину очереди.

Сетевые инженеры хорошо знакомы с графиком, представленным на рис. 7.5. Они интерпретируют этот график как зависимость задержек в сети от ее загрузки. Параметр модели соответствует коэффициенту использования сетевого ресурса, который участвует в передаче трафика, то есть выходного интерфейса коммутатора.

В приведенном графике есть и нечто неожиданное. Трудно представить, что обслуживающее устройство (сетевой ресурс) практически перестает справляться со своими обязанностями, когда его коэффициент использования приближается к 1. Ведь в этом случае нагрузка не превышает его возможностей, а только приближается к этому пределу. Интуитивно не очень понятна также причина существования очередей при значениях 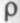в окрестностях 0,5. Интенсивность обработки трафика вдвое превышает интенсивность нагрузки, а очереди существуют!

Такие парадоксальные, на первый взгляд, результаты характерны для систем, в которых протекают случайные процессы. Так как 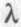и 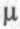— это средние значения интенсивностей потоков на больших промежутках времени, то на небольших промежутках времени они могут существенно отклоняться от этих значений. Очередь создается на тех промежутках, на которых интенсивность поступления пакетов намного превосходит интенсивность обслуживания.

Перегрузка ресурсов может привести к полной деградации сети, когда, несмотря на то, что сеть передает пакеты, полезная скорость передачи данных оказывается равной нулю. Это происходит в том случае, если задержки доставки всех пакетов превосходят некоторый порог, и пакеты по тайм-ауту отбрасываются узлом назначения, как устаревшие. Если же протоколы, работающие в сети, используют надежные процедуры передачи данных на основе квитирования и повторной передачи утерянных пакетов, то процесс перегрузки будет нарастать лавинообразно.

Существует еще один важный параметр, оказывающий непосредственное влияние на образование очередей в сетях с коммутацией пакетов. Этим параметром является вариация интервалов входного потока пакетов, то есть пульсация входного трафика. Мы анализиро­вали поведение модели теории очередей в предположении, что входной поток описывается пуассоновским распределением, которое имеет довольно большое стандартное отклонение

вариации (напомним, что средняя вариация его равна T при среднем значении интервала Т, а коэффициент вариации равен 1). А что будет, если вариация интервалов входного потока будет меньше? Или входной поток окажется сверхпульсирующим?

К сожалению, модели теории очередей не дают для этих случаев простых аналитических зависимостей, подобных формуле (1). Поэтому для получения результатов приходится применять методы имитационного моделирования сетей или проводить измерения в ре­альной сети.

На рисунке 7.7 показано семейство зависимостей 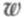от , полученных для разных значений коэффициента вариации CV входного потока. Имитационная модель учитывает фиксиро­ванную задержку в сети. Одна из кривых, у которой CV = 1, соответствует пуассоновскому входному потоку. Из рисунка видно, что чем меньше пульсирует входной поток (CV приближается к нулю), тем меньше проявляется эффект лавинообразного образования очереди при приближении коэффициента загрузки ресурса к 1. И наоборот, чем больше CV, тем раньше (при меньших значениях ) начинает этот эффект проявляться.

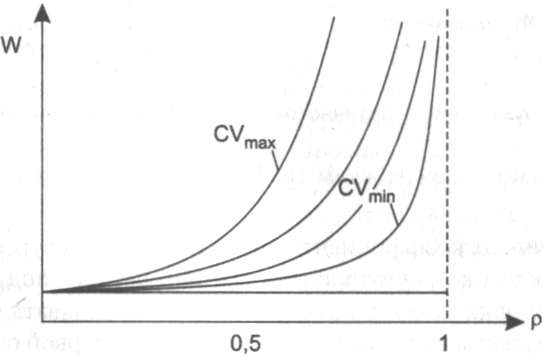
Рис. 7.7. Влияние степени пульсации потока на задержки

Из поведения графиков на рисунке можно сделать два вывода: во-первых, для оценки значений задержек в очередях на коммутаторах сети недостаточно информации о коэффициенте загрузки 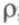, необходимо также знать параметры пульсации трафика; во-вторых, для снижения уровня задержек нужно снижать значение 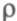и уменьшать пульсацию трафика.