Топология физических связей

Объединяя в сеть несколько (больше двух) компьютеров, необходимо решить, каким образом соединить их друг с другом, другими словами, выбрать конфигурацию физических связей, или топологию.

Под топологией сети понимается конфигурация графа, вершинам которого соответствуют конечные узлы сети (например, компьютеры) и коммуникационное оборудование (например, маршрутизаторы), а ребрам — физические или информационные связи между вершинами.

Число возможных вариантов конфигурации резко возрастает при увеличении числа связываемых устройств. Так, если три компьютера мы можем связать двумя способами (рис. 2.9, а), то для четырех можно предложить уже шесть топологически разных конфигураций (при условии неразличимости компьютеров), что и иллюстрирует рис. 2.9, б.

Мы можем соединять каждый компьютер с каждым или же связывать их последовательно, предполагая, что они будут общаться, передавая сообщения друг другу «транзитом». Транзитные узлы должны быть оснащены специальными средствами, позволяющими им выполнять эту специфическую посредническую операцию. В качестве транзитного узла может выступать как универсальный компьютер, так и специализированное устройство.

Рис. 2.9. Варианты связи компьютеров

От выбора топологии связей существенно зависят характеристики сети. Например, наличие между узлами нескольких путей повышает надежность сети и делает возможным распределение загрузки между отдельными каналами. Простота присоединения новых узлов, свойственная некоторым топологиям, делает сеть легко расширяемой. Экономические соображения часто приводят к выбору топологий, для которых характерна минимальная суммарная длина линий связи.

Среди множества возможных конфигураций различают полносвязные и неполносвязные.

Полносвязная топология (рис. 2.10, а) соответствует сети, в которой каждый компьютер непосредственно связан со всеми остальными. Несмотря на логическую простоту, этот вариант оказывается громоздким и неэффективным. Действительно, в таком случае каждый компьютер в сети должен иметь большое количество коммуникационных портов, достаточное для связи с каждым из остальных компьютеров сети. Для каждой пары компьютеров должна быть выделена отдельная физическая линия связи. (В некоторых случаях даже две; если невозможно использование этой линии для двусторонней передачи.) Полносвязные топологии в крупных сетях применяются редко, так как для связи N узлов требуется N(N - 1)/2 физических дуплексных линий связей, то есть имеет место квадратичная зависимость от числа узлов. Чаще этот вид топологии используется в многомашинных комплексах или в сетях, объединяющих небольшое количество компьютеров.

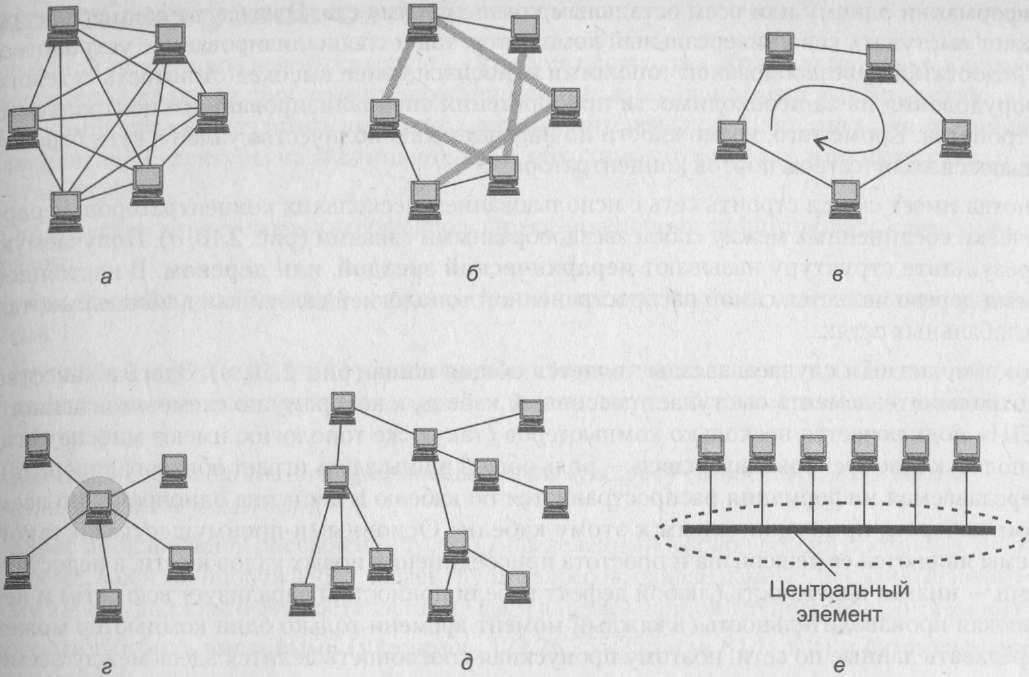
Рис. 2.10. Типовые топологии сетей

Все другие варианты основаны на неполносвязных топологиях, когда для обмена данными между двумя компьютерами может потребоваться транзитная передача данных через другие узлы сети.

Ячеистая топология [5] получается из полносвязной путем удаления некоторых связей (рис. 2.10, б). Ячеистая топология допускает соединение большого количества компьютеров и характерна, как правило, для крупных сетей.

В сетях с кольцевой топологией (рис. 2.10, в) данные передаются по кольцу от одного компьютера к другому. Главным достоинством кольца является то, что оно по своей природе обеспечивает резервирование связей. Действительно, любая пара узлов соединена здесь двумя путями — по часовой стрелке и против нее. Кроме того, кольцо представляет собой очень удобную конфигурацию для организации обратной связи — данные, сделав полный оборот, возвращаются к узлу-источнику. Поэтому источник может контролировать процесс доставки данных адресату. Часто это свойство кольца используется для тестирования связности сети и поиска узла, работающего некорректно. В то же время в сетях с кольцевой топологией необходимо принимать специальные меры, чтобы в случае выхода из строя или отключе­ния какого-либо компьютера не прерывался канал связи между остальными узлами кольца.

Звездообразная топология (рис. 2.10, г) образуется в случае, когда каждый компьютер подключается непосредственно к общему центральному устройству, называемому концентратором [6]. В функции концентратора входит направление передаваемой компьютером информации одному или всем остальным компьютерам сети. В качестве концентратора может выступать как универсальный компьютер, так и специализированное устройство. К недостаткам звездообразной топологии относится более высокая стоимость сетевого оборудования из-за необходимости приобретения специализированного центрального устройства. Кроме того, возможности по наращиванию количества узлов в сети ограничиваются количеством портов концентратора.

Иногда имеет смысл строить сеть с использованием нескольких концентраторов, иерархически соединенных между собой звездообразными связями (рис. 2.10, д). Получаемую в результате структуру называют иерархической звездой, или деревом. В настоящее время дерево является самой распространенной топологией связей как в локальных, так и глобальных сетях.

Особым частным случаем звезды является общая шина (рис. 2.10, е). Здесь в качестве центрального элемента выступает пассивный кабель, к которому по схеме «монтажного ИЛИ» подключается несколько компьютеров (такую же топологию имеют многие сети, использующие беспроводную связь — роль общей шины здесь играет общая радиосреда). Передаваемая информация распространяется по кабелю и доступна одновременно всем компьютерам, присоединенным к этому кабелю. Основными преимуществами такой схемы являются ее дешевизна и простота присоединения новых узлов к сети, а недостатками — низкая надежность (любой дефект кабеля полностью парализует всю сеть) и невысокая производительность (в каждый момент времени только один компьютер может передавать данные по сети, поэтому пропускная способность делится здесь между всеми узлами сети).

В то время как небольшие сети, как правило, имеют типовую топологию — звезда, кольцо или общая шина, для крупных сетей характерно наличие произвольных связей между компьютерами. В таких сетях можно выделить отдельные произвольно связанные фрагменты (подсети), имеющие типовую топологию, поэтому их называют сетями со смешанной топологией (рис. 2.11).

Рис. 2.11. Смешанная топология