Рекурсивные алгоритмы работы с двоичными деревьями

Рекурсивное определение дерева. Представим, что отдельные дуги дерева ведут к частям дерева, которые сами являются деревьями. Такая точка зрения приводит к рекурсивному определению дерева. Дерево – это пустая структура или узел, связанный дугами с конечными числом деревьев. Прохождение дерева заключается в обходе всех его узлов. Рекурсивный алгоритм прохождения двоичного дерева будет таким:

1. Посетить корень.

2. Посетить левое поддерево.

3. Посетить правое поддерево.

Обходя дерево по этому алгоритму, мы посетим узлы по алфавиту (рис.14.8).

Рис.14.8. Порядок обхода дерева

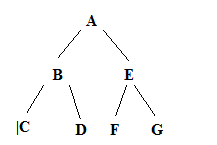Проходя дерево по данному алгоритму, мы посетим вершины дерева в следующем порядке: A, B, C, D, E, F, G. Как изменить порядок пунктов алгоритма, чтобы пройти узлы в последовательности:

а) A, E, G, F, B, D, C; б) C, D, B, F, G, E, A; в) C, B, D, A, F, E, G

П р и м е р ы использования рекурсивных алгоритмов для работы с двоичными деревьями.

const k = 13;

a:array[1..k] of integer=(2,4,6,1,3,5,7,10,12,14,11,13,15);

type ptree=^ttree;

ttree = record

dat:integer;

l,r:ptree

End;

Var

kor, t:ptree;

i, x: integer;

fl: boolean; {v - новый элемент}

procedure bild(v:ptree; var kor:ptree); {построение}

Begin

if kor = nil