Задача постановка метод алгоритм

Приведем пример построения алгоритма с одновременным ана­лизом его правильности.

Задача: Определить периметр треугольника, заданного на плос­кости координатами вершин.

X_С,У_С

X_А,У_А Xв,Ув

Постановка задачи

Определение периметра треугольника, заданного на плоскости.

Дано: А = (x_А, y_А)

В = (x_В, y_В) - координаты вершин треугольника

С = (x_С,y_С)

Треб.: Р - периметр

Метод решения

Р = L_АВ +L_ВС+L_СА

L_АВ = ,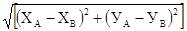

L_ВС =

L_СА =

где: Р = L(A,B) + L(B,C) + L(C,A);

здесь L[(x,y),(u,v)] = .

Приведем алгоритм, полученный из описания метода упорядоче­нием операций вычисления длин сторон треугольника с заверша­ющим вычислением периметра. Результаты выполнения алгоритма приведены справа.

алг «периметр треугольника»

Нач

LAB: =

LBC: =

LCA: =

Р:= LAB + LBC + LCA

Кон

Результаты

Р = LAB + LBC + LCA

Сравнение результатов выполнения алгоритма с описанием метода решения показывает, что это одна и та же система формул, что подтверждает правильность алгоритма.

Систематические методы анализа правильности алгоритмов и программ опираются на сопоставление тех же самых описаний, которые используются при их систематическом составлении.

Анализ правильности: