Xj V х2) (х2 V Хд) (Xg V X.,) ... (x^^i v хп) (xfl v Xi)

Xj V х2) (х2 V Хд) (Xg V X.,)... (x^^i v хп) (xfl v Xi).

Исходя из этого представления, получим минимальную схему (рис. 55).

Рис. 55.

9.16. Если бы такая П-схема существовала, то в ней каждой пере­менной соответствовал бы один контакт, причем — в силу решения задачи 9.14 — положительный. Тогда по 11-схеме можно было бы по­строить формулу, в которую каждая переменная входит по одному разу, а из операций используются лишь конъюнкции и дизъюнкции. Пусть последняя операция — дизъюнкция. Тогда функция /(х, у, г, I, и)= =--ху\^! tu V xzu v tzy представляется в виде f—fi V /₂, где f_x и /₂ не имеют общил переменных и не являются константами. Пусть переменная г входит в Положим у—1=0. Тогда / превращается в <р(х, г, и)=хги. Далее, функция /₂ при этом превратится в тождественный нуль, так как нет значений х, и, для которых <р равна 1 вне зависимости от зна­чения г, а /₂ от Z не зависит! Итак, /_г после указанной подстановки пере­ходит в xzu, а значит, в /’, входили (существенно) переменные х и и. Аналогично, полагая х=и= 0, получаем, что должна существенно зависеть от у и t. В результате в f₁ существенно входят все пять пере­менных, и мы пришли к противоречию.

Мы предоставляем читателю исключить аналогичным образом воз­можность представления f в виде /,/₂, где /\ и /₂ не имеют общих пере­менных и не являются константами.

9.17. а) Для реализации элементарной конъюнкции требуется п контактов. Число элементарных конъюнкций в СДНФ не превосходят 2". Значит, общее число контактов не превосходит п2”[46])

б) Рассматривается аналогично.

в) Число членов в СДНФ равно числу наборов, на которых функция равна 1, а число членов в СКНФ — числу наборов, на которых она равна 0. Одно из этих чисел не превосходит 2^й-1. Применяя соответст­венно способ а) или б), мы получим схему, в которой не более м 2"^-1 контактов.

9.18. Разложим функцию f(x_lt х._г, Х/г, х^. _{+ 1}) по переменной

х_к+1 (см (2.16)): f=x_k+lip(x_l, x_k) V л >+1 ^ (^............................. х_к). Если

функции, и 'ф уже реализованы, то функция f реализуется, как

показано ни рис. 56 Здесь через — р — и обозначены

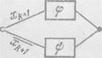схемы, реализующие <р и гр; их выходы отож­дествлены. Если для реализации функций от k переменных (в частности, <р и if) требуется не более Cf. контактов, то для реализации / тре­буется не более 2 q >,-|-2 контактов, т. е. ^cft-ri <2с_а-(-2. Если учесть теперь, что с_х = 1 (для функций от одной переменной хватает Рис. Е6. одного контакта), то получаем, что 2^ft-) -j-

-f 2*-¹+2*-²+2*-з+...+2²+2 = 3-2*-1—2. Таким образом, L (п) 3-2^,i_1—2.

9.19. 1. На рис. 41 мы видели, что контакты в схеме естественным образом распадаются на «этажи», причем в каждом этаже находятся контакты, связанные с какой-то одной переменной. Из рисунка видно также, что к каждому выходу идет лишь одна существенная цепь; она содержит но одному контакту из каждого этажа; каждой такой цепи соответствует некоторая полная правильная элементарная коиъюнкция, причем разным выходам соответствуют разные конъюнкции Таким образом, каждой элементарной конъюнкции соответствует некоторый выход.

Строгое доказательство проводится по индукции. Пусть уже дока­зана универсальность (1, 2 *)-полюсника; докажем универсальность (1, 2*⁺¹)-полюсника Из предположения индукции следует, что каждо­му выходу (1, 2 *)-полюсника соответствует единственная существенная цепь, представляющая некоторую полную элементарную конъюнкцию от k переменных, причем разным выходам отвечают разные конъюнк­ции. Каждый выход (1, 2*⁺¹)-полюсника связан с единственным выходом (1, 2 *)-полюсника, причем с одним выходом (1, 2 ^л)-полюсника связаны два выхода (1, 2 *^{+ 1})-полюсника: один — контактом х_{к + 1}, другой — контактом ₊₁. Отсюда следует, что на каждом выходе (1, 2*+ ¹)-по- люсника реализуется своя полная элементарная конъюнкция.

2. Пусть нам нужно реализовать функцию f(x_lt..., х_п). Представим ее в виде СДНФ. Отождествим у универсального (1, 2^п)-полюсника выходы, на которых реализуются элементарные конъюнкции, входящие
в СДНФ. Объявим получившийся в результате полюс выходом схемы. Ясно, что полученная схема реализует /(х_х, ..., х_п).

Число контактов в этой схеме равно числу контактов в универ­сальном (I, 2 ^п)-полюсиике, т. е.

2-t-4 + 8+. +2«= 2» + ¹ — 2.

Мы получае