 |
Главная Случайная страница Контакты | Мы поможем в написании вашей работы! | |
Нейтральные мутации и дрейф генов
|
|
Каждый ген в генофонде популяции может существовать в виде нескольких вариантов – аллелей. В результате мутаций возникают новые аллели (старых генов). Термины «мутация» и «аллель» генетики часто смешивают. Это жаргон, но все привыкли. Поэтому часто говорят «мутация распространилась в популяции», хотя более правильно – «аллель распространился в популяции».
Нейтральные мутации – не влияют на приспособленность.
Приспособленность – это эффективность размножения.
Например, если каждый носитель аллеля а1 оставляет в среднем 5 жизнеспособных потомков, а каждый носитель аллеля а2 (т.е. другого варианта того же гена А) оставляет в среднем 4 столь же жизнеспособных потомков, то приспособленность аллеля А1 по отношению к аллелю А2 = 5/4 = 1.25
Fa1/Fa2 = 1.25
Как правило, абсолютную приспособленность не измеряют – это не очень понятно, как сделать. А вот относительную приспособленность померить можно: просто посмотреть, с какой скоростью размножаются носители данного аллеля по сравнению со всеми остальными (т.е. с теми, у кого этого аллеля нет).
Различие между аллелями а1 и а2 – не нейтральное. Аллель а1 – «лучше», чем а2 (он повышает приспособленность).
Если же Fa1/Fa2 ≈ 1, то это нейтральное различие. Если в генофонде был сначала только аллель а1, а потом в результате мутации появился аллель а2, причем Fa1/Fa2 ≈ 1, то это значит, что мутация, в результате которой возник аллель а2, была нейтральной.
Разберемся, как будет меняться частота нейтральной мутации (нейтрального аллеля) со временем, с течением поколений.
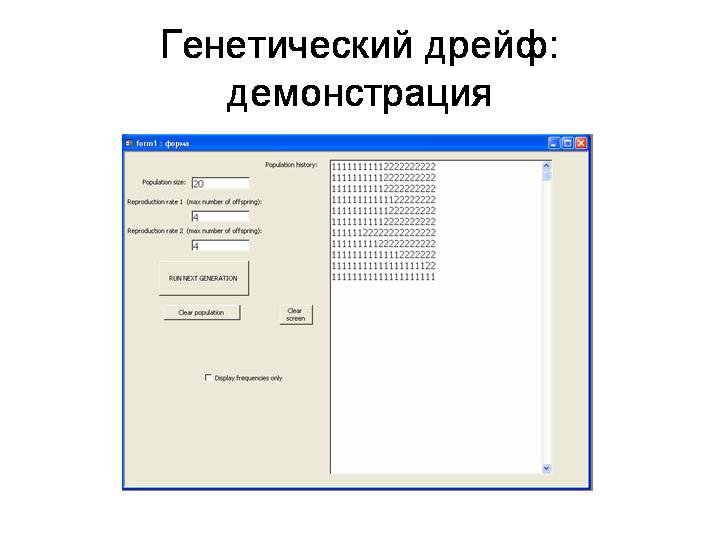
Демонстрация на модели «Genetic drift» (при параметрах 20, 4, 4). Устройство модели: Популяция из N гаплоидных особей. Два нейтральных аллеля: 1 и 2. В начальный момент времени частоты аллелей равны (q1=q2=0.5). Каждая особь производит потомков (случайное число в диапазоне от 0 до укузанного числа). Из этих потомков затем случайным образом отбирается N «выживших», которые и формируют следующее поколение в модельной популяции.
Выводы:
· Частота нейтрального аллеля в популяции изменяется по закону случайных блужданий. A random walk is a mathematical formalisation of a trajectory that consists of taking successive random steps. Случайные колебания частот аллелей, не связанные с действием отбора, называются генетическим дрейфом.
· Конечный исход этих случайных блужданий строго предопределен. Это всегда одно из двух: либо аллель зафиксируется (достигнет частоты q=1), либо он элиминируется (достигнет частоты q=0). Третьего не дано. Одно из двух событий рано или поздно ОБЯЗАТЕЛЬНО произойдет. Случайно блуждая, частота аллеля непременно когда-нибудь наткнется либо на верхнюю планку (фиксация), либо на нижнюю (элиминация).
Формула 1. Чему равна вероятность фиксации (Pfix) нейтральной мутации? Если исходная частота q=0.5, то совершенно ясно, что аллель с равной вероятностью зафиксируется или элиминируется, т.е. Pfix = 0.5.
Представим себе ситуацию, когда у нас исходно есть не 2, а 4 нейтральных аллеля с одинаковыми частотами: q1=q2=q3=q4=0.25
Легко увидеть, что конечным результатом дрейфа будет фиксация одного из аллелей и элиминация трех других. Это становится ясно, если понять, что мы имеем полное право временно и условно объединить три из четырех аллелей в один, комплексный. Например, давайте считать, что у нас есть два аллеля: 1 и не-1. Аллель «не-1» – это общее название для аллелей 2, 3 и 4. Про два аллеля мы уже знаем, что один из них рано или поздно обязательно зафиксируется, а другой элиминируется. Стало быть, у нас либо зафиксируется аллель 1, либо «не-1». В первом случае все ясно – один аллель зафиксировался, три элиминировались. Во втором – у нас осталось три аллеля (2, 3 и 4). Давайте представим эту ситуацию в виде двух аллелей: 2 и не-2. И так далее.
Таким образом, можно считать доказанным, что конечным результатом дрейфа будет фиксация одного из аллелей и элиминация трех других. Ясно, что, поскольку исходно все 4 аллеля были в абсолютно равном положении, шансы на фиксацию у них должны быть одинаковы. В сумме эти шансы дают 1 (один из аллелей точно зафиксируется).
Следовательно, Pfix1 = Pfix2 = Pfix3 = Pfix4 = ј = 0.25
Вероятность фиксации нейтрального аллеля равна его исходной частоте (т.е. частоте в тот момент, для которого мы пытаемся рассчитать вероятность).
Поскольку мы могли с тем же успехом взять не 2, не 4, а любое другое число нейтральных аллелей, очевидно, что:
Pfix = q
Вероятность фиксации нейтрального аллеля равна его частоте. Это первая из трех формул, которую мы с вами должны вывести. А чему равна вероятность элиминации аллеля? Очевидно, 1-q.
Формула 2. Следующий очень важный вопрос – определить, сколько нейтральных мутаций будет фиксироваться в популяции в каждом поколении. Если мы сможем это установить, то мы обретем великий инструмент – молекулярные часы. Зная, с какой скоростью фиксируются в популяции нейтральные мутации, и зная, сколько их накопилось за какой-то период, мы сможем вычислить длительность этого периода. Например, сколько разных нейтральных мутаций есть в геномах человека и шимпанзе? Это можно подсчитать. Если бы мы еще знали, с какой скоростью фиксируются нейтральные мутации, мы могли бы на основе данных о числе накопившихся мутаций вычислить, как давно разошлись эволюционные линии предков человека и шимпанзе, понять, когда жил их последний общий предок.
Итак, сколько же нейтральных мутаций будет фиксироваться в популяции за одно поколение? Вывод этой формулы – это абсолютнейший шедевр биологической математики. Надеюсь, вы оцените.
Итак, от чего зависит скорость накопления нейтральных мутаций?
Очевидно, она зависит от того, с какой скоростью они появляются – то есть от скорости нейтрального мутагенеза, а также от того, какая часть вновь появляющихся нейтральных мутаций будет фиксироваться (а не элиминироваться).
Обозначим переменные:
· V – искомая величина: среднее количество нейтральных мутаций, которые будут фиксироваться в генофонде популяции за одно поколение.
· M – темп появления новых нейтральных мутаций (на всю популяцию). Это среднее количество новых нейтральных мутаций, появляющихся в популяции за одно поколение.
· m – то же, в расчете на одну особь. Это среднее количество новых нейтральных мутаций, имеющихся в геноме родившейся особи. Эту величину реально можно измерить.
· Pfix – доля (или процент) возникших в популяции нейтральных мутаций, которые в конечном счете зафиксируются. Эта доля, очевидно, есть то же самое, что вероятность фиксации такой мутации.
· N – численность популяции. Это тоже можно измерить (правда, она могла меняться в прошлом, и мы не знаем, как она менялась – это плохо).
Приступим к выводу формулы.
Очевидно, что V = M• Pfix
Искомая величина V равна числу мутаций, появляющихся за поколение, умноженному на ту долю, которая зафиксируется из них в конечном счете.
Чему равно M? Очевидно, что M = N•m
Это, надеюсь, ясно без пояснений.
А как найти Pfix, т.е. как выразить эту величину через те величины, которые можно измерить? Ну, мы ведь уже знаем, что Pfix = q, т.е. для каждой мутации вероятность зафиксироваться равна частоте этой мутации в данный момент. Новая, только что появившаяся мутация, очевидно, изначально есть только у одной особи. То есть ее частота q=1/N. Следовательно, и вероятность ее фиксации равна 1/N. Следовательно, из всех новых мутаций зафиксируется их часть, равная 1/N. Вот вам и искомое значение Pfix:
Pfix = q = 1/N
Итак, имеем:
V = M• Pfix M = N•m Pfix =1/N
Подставляем в первую формулу две другие, получаем:
V = N•m/N
Численность популяции великолепным образом сокращается! Итого:
V = m
Это и есть Вторая Великая Формула, и, наверное, самый блистательный образчик «биологической математики». Скорость фиксации нейтральных мутаций не зависит от численности популяции! Она равна m, т.е. просто-напросто скорости мутагенеза, скорости появления нейтральных мутаций в расчете на одну особь.
Поэтому у нас есть молекулярные часы. Мы их имеем благодаря генетическому дрейфу и благодаря тому, что многие мутации нейтральны. Принцип молекулярных часов:
D = 2V•t
где D – количество нейтральных различий между двумя видами, t – время, прошедшее с тех пор, когда жил последний общий предок этих двух видов. Двойка тут появляется потому, что нейтральные мутации накапливались обоими видами. Каждый из них накопил за время t количество нейтральных мутаций, равное D/2.
----------------------------------------------
Дарвин (рекомендации по эссе).

Главный вклад Дарвина в умственное развитие человечества. До Дарвина нам был известен только ОДИН механизм возникновения сложных объектов, предназначенных для какой-то цели или функции – разумный дизайн. Пейли и часы. Все подобные объекты трактовались как результат чьего-то сознательного проектирования. Или придумывались некие невнятные дополнительные сущности – жизненная сила, стремление к совершенству и т.п. (ламаркизм, номогенез). Что с научной точки зрения ничуть не лучше гипотезы о разумном дизайне. Дарвин открыл другой механизм – механизм самопроизвольного возникновения сложных объектов, приспособленных для выполнения функций – объектов, которые выглядят (для нас) так, как будто бы их кто-то нарочно спроектировал.
Философские аспекты: Dennett “Darwin’s Dangerous Idea”. Физики и химики подтянулись позже. Вдохновленный успехом нелинейной неравновесной термодинамики, Эйген в нобелевской речи даже назвал Дарвина с его идеей естественного отбора «великим физиком». Лаплас. До Дарвина биологи нуждались «в этой гипотезе». После Дарвина они могут без нее обойтись.
Дата публикования: 2014-10-20; Прочитано: 1016 | Нарушение авторского права страницы | Мы поможем в написании вашей работы!
