 |
Главная Случайная страница Контакты | Мы поможем в написании вашей работы! | |
Бюджетные ограничения
|
|
Бюджетное ограничение потребителя
Рассмотрим множество всех доступных потребителю товарных наборов при условии, что он располагает какой-то фиксированной денежной суммой М (money).
Очевидно, потребитель может купить количество товаров
x1, х2, х3, …, хn
по ценам соответственно:
Р1, Р2, Р3, …, Рn,
если выполняется условие:
Р1x1 + Р2х2 + Р3х3 + … + Рnxn £ M (*)
Выражение (*) называют бюджетным ограничением потребителя. Чтобы можно было изобразить данное условие графически, рассмотрим случай, когда потребительский выбор ограничен двумя товарами Х и Y.
Тогда бюджетное ограничение имеет вид:
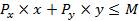 .
.
Бюджетная линия
Очевидно, что граница множества товарных наборов аналитически может быть записана уравнением:
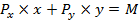
Эта граница называется бюджетной линией.
Предположим, что цены товаров не зависят от потребителя и выступают как внешние, постоянные заданные рынком величины. Тогда уравнение бюджетной линии можно представить в виде:
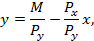
то есть в виде у = а – bх. Значит бюджетная линия соответственно представляет прямую линию АВ (рис. 4-7).
Координаты точек А(0;М/Рy) и В(М/Рx;0) характеризуют максимальные количества товаров Х и Y, которые может приобрести потребитель, потратив весь свой доход только на товар Х или только на товар Y.
Любой другой точке С, находящейся на бюджетной линии, соответствует набор товаров с = (хс; yс), который имеет стоимость М, то есть
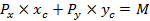
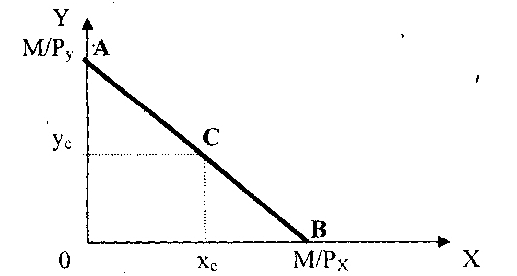
| Рис. 4-7. Бюджетная линия |
Бюджетная линия – это геометрическое место точек, характеризующих все наборы товаров, которые может приобрести потребитель, полностью израсходовав весь свой доход М при данных ценах товаров РX и РY.
Бюджетная линия имеет отрицательный наклон, так как Рx > 0, Рy > 0. Наклон бюджетной линии постоянен, так как Рx и Рy постоянны.
Множество всех наборов товаров, удовлетворяющих бюджетному ограничению, представляет собой треугольник АВО, ограниченный бюджетной линией и осями координат.
Дата публикования: 2014-10-20; Прочитано: 1172 | Нарушение авторского права страницы | Мы поможем в написании вашей работы!
