 |
Главная Случайная страница Контакты | Мы поможем в написании вашей работы! | |
Доказательство
|
|
Чтобы после раскрытия скобок получился одночлен 
, нужно выбрать те 
скобок, из которых берется 
, те 
скобок, из которых берется 
и т.д. и те 
скобок, из которых берется . Коэффициент при этом одночлене после приведения подобных членов равен числу способов, которыми можно осуществить такой выбор.
Первый шаг последовательности выборов можно осуществить 
способами, второй шаг — 
, третий —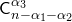 
и т.д., 
-й шаг — 
способами. Искомый коэффициент равен произведению
3.Формулы включений и исключений.характеристические функции мнежества.
· Характеристическая функция подмножества — функция с областью значений {0, 1}, вычисляемая для любого элемента содержащего его множества, результатом которой является число, обозначающее принадлежность элемента подмножеству.
Если элемент множества принадлежит подмножеству, значение характеристической функции равно единице, если же нет — нулю.
Свойства:
1. 
* 
= 
2. 
3.. 
+ - 
*
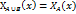4. 
5. 
, 
Комбинируя выписанные три формулы получим фориулу включений и исключений для m+1 свойств a1,a2,….,am,am+1.Что и требовалось доказать. □
4.Разбиения.Числа Стерлинга 1 и 2 рода. Свойства чисел Стерлинга. Числа Белла.
Под разбиением n-элементного множества A на k блоков будем понимать произвольное семейство π = {B1 ,…,Bk}, такое, что B1 U … U Bk = A, Bi ∩ Bj = Ø для 1≤i≤k. Подмножества B1,…,Bk будем называть блоками семейства π. Множество всех разбиений множества А на k блоков будем обозначать Пk(A), а множество всех разбиений через П(А).
Число Стирлинга второго рода S (n, k) есть число разбиений n-элементного множества на k блоков: S (n, k) = |Пk (A)|, где |А| = n.
Дата публикования: 2014-10-20; Прочитано: 567 | Нарушение авторского права страницы | Мы поможем в написании вашей работы!
