 |
Главная Случайная страница Контакты | Мы поможем в написании вашей работы! | |
Определение и составляющие экономического механизма
|
|
Экономический механизм – это большая и сложная система, предназначенная для осуществления ориентированной, направленной деятельности отдельных субъектов и других экономических агентов и организаций на достижение общих для всех целей. Тем самым преодолевается на микроуровне стихийность, вызванная как случайностями в течении природных процессов, так и наличием собственных интересов у индивидуумов (отдельных производителей) и других более крупных экономических единиц (так называемое правило «невидимой руки»).
Математические модели, используемые для анализа экономического механизма, выходят за рамки общепринятых в курсах экономико-математических методов. Таким моделям в настоящем разделе уделено особое внимание.
При построении математических моделей экономического механизма прежде всего необходимо на формализованном уровне описать систему организационных, правовых, экономических и финансовых процедур и правил, использующихся и не использующихся в экономической практике, но в последнем случае представляющих научный интерес для исследования.
Далее, надо уметь на формализованном уровне (математических или в виде имитирующих алгоритмов) описать реакцию отдельных людей или целых коллективов на различные аспекты экономического механизма. Это означает, что должны быть разработаны принципы построения математических моделей, достаточно адекватно описывающие интересы людей и организаций, и учитывающие социальные и психологические факторы, которые воздействуют на принятие решений в реальности. Следует учитывать, что принципы математического моделирования экономического поведения людей разработаны крайне в недостаточной степени.
Для решения проблем математического описания экономических механизмов в науке предлагаются разнообразные подходы и методы. Мы рассмотрим ограниченный, но весьма важный вопрос о моделировании взаимоотношений между производственной единицей (напр., предприятием) и вышестоящей организацией (руководством фирмы, министерства). При этом не будем затрагивать всю структуру их отношений, а ограничимся проблемой стимулирования рационального использования производственных ресурсов. Практическая важность этой проблемы очевидна, она поставлена Я.Корнаи и Т.Липтаком, после чего ею занимались многие специалисты.
Как следствие, имеется значительное число разнообразных подходов и направлений к анализу даже этой, ограниченной, проблемы. Каждое из направлений обладает собственной системой понятий и собственными методами исследования тех или иных аспектов проблемы. Поэтому в начале каждого раздела на основе одной простой и довольно условной модели системы производственных единиц будет дано представление о применяемых методах, а затем, если это окажется возможным, могут быть кратко описаны модели и результаты, которые были получены в соответствующих направлениях.
В качестве стандартной модели рассмотрим модель двухуровневой системы, структурная схема которой приведена на рис.6.1.
| Центр |
| Внешняя среда |
| Производственная единица 1 |
| Производственная единица 2 |
| Производственная единица n |
| … |
| … |
| … |
| Рис.6.1 Схема двухуровневой производственной иерархической структуры |
В модели имеется n производственных единиц, руководство которыми осуществляется вышестоящей организацией (Центром). Блок «Внешняя среда» описывает воздействие на систему со стороны природы и других экономических систем. Пусть для простоты каждая производственная единица производит единственный продукт, используя для этого единственный ресурс.
Производство в i-й производственной единице опишем на основе концепции множества технологических возможностей, имеющего вид (рис.6.2), где:
yi - выпуск продукции, xi - затраты ресурса, Ai – эффективность использования единицы ресурса (таким ресурсом может быть численность рабочих на предприятии или отработанное ими количество человеко-часов).
Задача Центра состоит в распределении ресурса между производственными единицами, причем в различных подходах возможности Центра и используемые им методы будут описываться различным образом, в зависимости от используемых концепций.
Рис.6.2 Множество технологических возможностей
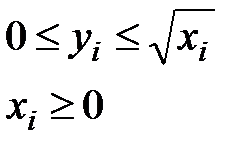
yi **
Ai
yi
xi***
xi
C
{ -q, p }
6.2. Классический подход к анализу экономических механизмов
6.2.1. Простая модель
Модели, излагаемые в п.6.2, основаны на предположении о полной информированности Центра о возможностях производственных единиц. Пусть задача, стоящая перед Центром, состоит в таком распределении заданий отдельным производственным единицам, которое приводило бы к заранее заданному суммарному выпуску продукции Y* при минимальных затратах ресурса. При этом необходимо построить такую систему стимулирования производства, которая делала бы план распределения ресурсов и выпуска продукции, выбранный Центром, наиболее предпочтительным и для производственных единиц, т.е. необходимо построить систему стимулирования, согласованную с планом.
В соответствии с рис.6.2 предполагается, что множество производственных возможностей предприятий имеет вид
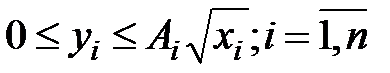 (6.1)
(6.1)
причем известны величины Ai, отражающие эффективность производства отдельных единиц, известны Центру. Центр распределяет ресурс исходя из того, что производственные единицы используют полученные ресурсы эффективно, т.е.
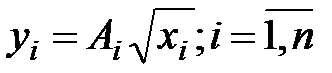 . (6.2)
. (6.2)
Выполнение объема производства на уровне необходимого выпуска (напр., рыночного спроса Y*) запишем в виде:
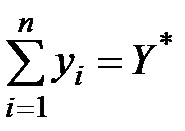 . (6.3)
. (6.3)
Требование экономии производственных ресурсов приводит к следующей формулировке целевой функции Центра:
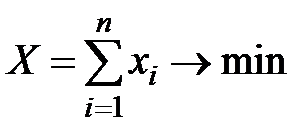 (6.4)
(6.4)
Для решения задачи (5.2)-(5.4), т.е. выбора такого варианта распределения ресурса 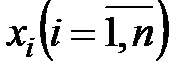 и соответствующих производственных заданий
и соответствующих производственных заданий 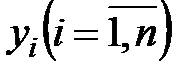 , связанных с xi соотношением (5.2), можно использовать метод множителей Лагранжа.
, связанных с xi соотношением (5.2), можно использовать метод множителей Лагранжа.
Функция Лагранжа имеет вид
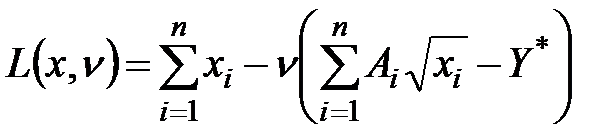 , (6.5)
, (6.5)
где ν – множитель Лагранжа.
Для нахождения решения задачи (6.2)-(6.4) надо удовлетворить необходимому условию оптимальности – найти стационарные точки функции Лагранжа, т.е. точки (x*,ν*), в которых выполняются условия. (x*= x1*, x2*,…, xn*):
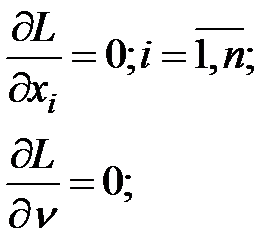
и проверить, что в них достигается минимум функции (6.4).
Так как
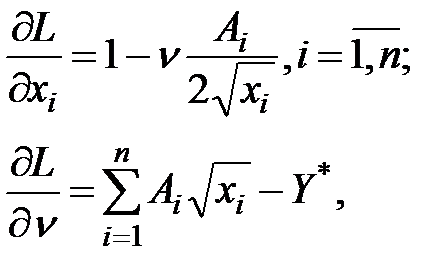
то стационарная точка (x*,ν*) удовлетворяет соотношениям
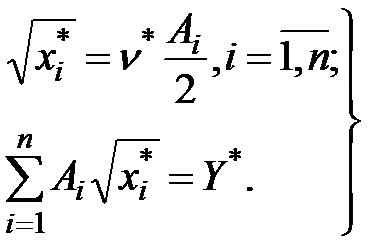 (6.6)
(6.6)
Из этих соотношений сразу следует, что
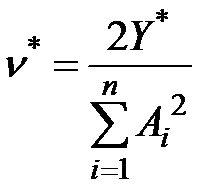 . (6.7)
. (6.7)
В силу вогнутости кривых производственных возможностей на рис.8, стационарная точка функции Лагранжа в данном случае (6.7) соответствует минимуму X. Поэтому оптимальное распределение ресурсов и производственные задания, соответствующие этому распределению ресурсов, имеют вид:
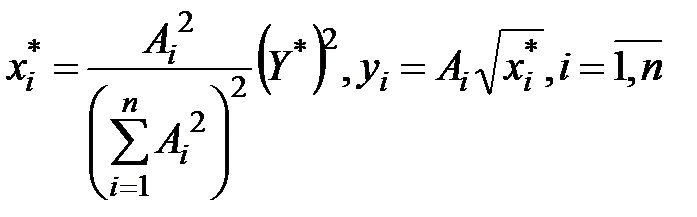 (6.8)
(6.8)
Суммарное потребление ресурса при этом имеет значение
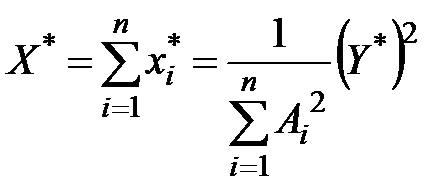 .
.
Распределение ресурсов и плановых заданий для производственных единиц, описываемое соотношениями (6.8), является оптимальным для Центра.
В какой степени это распределение соответствует интересам отдельных производственных единиц? Иначе управление будет носить административно-приказной, а не экономический характер, построенный на заинтересованности производителей.
Для этого необходимо описать интересы производителей. Наиболее часто предполагается, что на ресурсы и продукцию задаются цены, которые обозначим q и p соответственно. Причем производственные единицы влияния на цены не оказывают (условия, близкие к совершенной конкуренции). Считается, что производственные единицы заинтересованы в увеличении прибыли
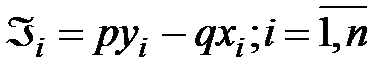 . (6.9)
. (6.9)
Заинтересованность в увеличении прибыли может быть основана на том, что материальное положение и вытекающие из него различные льготы сотрудникам растут с ростом прибыли (6.9).
Чтобы оценить производственное задание и объемы ресурсов, в которых заинтересована производственная единица, рассмотрим, какой объем ресурсов и выпуск продукции приводит к максимизации прибыли (5.9) в случае, когда множество производственных возможностей описывается соотношением (6.1). Отметим, что при любом фиксированном Центром объеме ресурсов xi максимум прибыли при любых положительных ценах q и p достигается при 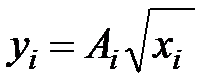 , т.е. когда производственные возможности используются полностью. Поэтому задача максимизации (6.9) при условии (6.1) эквивалентна задаче максимизации (6.9) при условии (6.2), т.е. надо максимизировать
, т.е. когда производственные возможности используются полностью. Поэтому задача максимизации (6.9) при условии (6.1) эквивалентна задаче максимизации (6.9) при условии (6.2), т.е. надо максимизировать
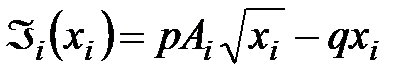
Поскольку необходимое условие максимума имеет вид
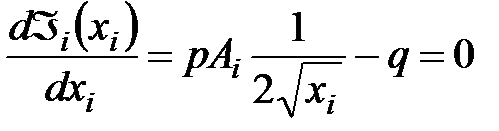 , (6.10)
, (6.10)
то разрешая уравнение (6.10) относительно xi, оптимальное количество ресурсов и соответствующий выпуск продукции yi при данных ценах q и p и 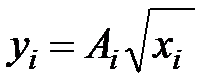 будут равны
будут равны
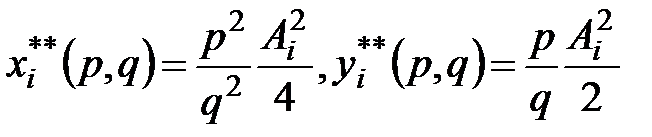 . (6.11)
. (6.11)
Если цены q и p произвольны, то потребность в ресурсах xi** и выпуск продукции yi** не будут совпадать с величинами xi* и yi*, предпочтительными с точки зрения Центра. Это обычно приводит ко всевозможным действиям производственных единиц в части перераспределения ресурса в своих интересах. Поэтому целесообразно установить такие цены (по крайней мере, внутренние, в пределах фирмы, управляемой Центром), при которых распределение ресурсов, оптимальное для Центра, было бы оптимальным и для отдельных производственных единиц. Приравнивая формулы (6.6) и (6.11), легко заметить, что для этого достаточно положить
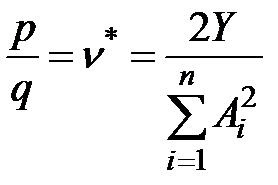 . (*)
. (*)
Из этого соотношения вытекает экономический смысл оптимального значения множителя Лагранжа ν*: это такое соотношение цен ресурсов и внутренних цен продукции, при котором интересы Центра и отдельных производственных единиц совпадают. Остается сопоставить внутренние цены с рыночными, и проблема согласования решений в двухуровневой рыночной экономической системе будет согласована в полной мере.
Пусть q*>0 – произвольная цена продукции. Положим p*=ν*q*. Тогда
xi**(p*,q*)=xi*, yi**(p*,q*)=yi* для всех i.
Таким образом, система стимулирования оказывается согласованной с системой планирования производства при p= p* и q=q*.
Рассмотрим теперь произвольные цены q и p. На рис.6.2 изображена точка (xi**,yi**), оптимальная для i-го предприятия при данных ценах. Изменяя цены (неотрицательные!), можно сделать оптимальным для предприятия любое сочетание затрат и выпусков, принадлежащее кривой ОС, которая характеризует эффективное использование ресурса. Таким образом, Центр может назначить любой эффективный для i-го предприятия план затрат ресурсов и выпуска продукции (xi, yi). При этом Центр может сделать с помощью цен выгодным его выполнение вне зависимости от того, был ли этот план получен на основе решения задачи (6.2)-(6.4) или некоторой другой задачи оптимизации, либо же он был назначен с помощью какой-либо неформализованной процедуры. При этом цены для i-го предприятия pi и qi могут не совпадать при различных i. Может возникнуть затруднение: цены приходится назначать для каждого предприятия в отдельности. Таким образом, переход от величин, полученных на основе задачи оптимизации (6.2)-(6.4), к произвольным эффективным для предприятия величинам (xi, yi) приводит к потере важного свойства системы стимулирования – единых цен на ресурсы и продукцию. С экономической точки зрения такая дифференциация цен может оказаться неприемлемой (дискриминация производителей), поэтому обсудим вопрос о том, в каких случаях удается сохранить единые цены.
6.2.2. Условия сохранения единых цен
Рассмотрим множество G таких значений суммарных затрат ресурсов 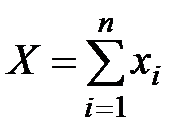 и выпусков
и выпусков 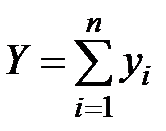 , которые могут быть реализованы изучаемой системой предприятий с производственными возможностями, описываемыми соотношениями (6.1).
, которые могут быть реализованы изучаемой системой предприятий с производственными возможностями, описываемыми соотношениями (6.1).
Вид множества G можно представить себе, исходя из следующих соображений. Во-первых, множество G выпукло. Во-вторых, в силу 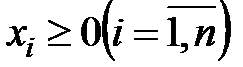 выполняется условие
выполняется условие 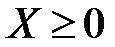 . В-третьих, при любых
. В-третьих, при любых 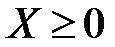 продукция, согласно (6.1), должна быть неотрицательной, т.е. нижняя граница множества G имеет вид луча
продукция, согласно (6.1), должна быть неотрицательной, т.е. нижняя граница множества G имеет вид луча 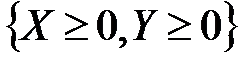 . Наконец, верхнюю границу множества G можно описать на основе решения задачи (6.2)-(6.4), которое имеет вид (6.8). Т.е. минимальные затраты ресурсов X* зависят от суммарного выпуска Y* следующим образом:
. Наконец, верхнюю границу множества G можно описать на основе решения задачи (6.2)-(6.4), которое имеет вид (6.8). Т.е. минимальные затраты ресурсов X* зависят от суммарного выпуска Y* следующим образом:
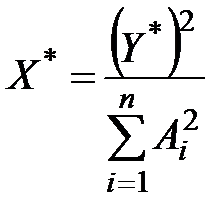 .
.
Это позволяет построить кривую минимальных затрат, т.е. зависимость X* от Y*.
Обратная функция
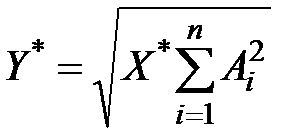 (**)
(**)
задает кривую зависимости максимального выпуска продукции от затрат.
Таким образом, множество G имеет вид (рис.6.3)
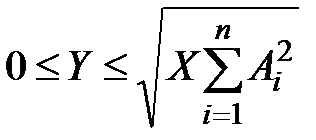 ,
,
Рис.6.3
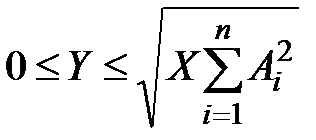
|
| y |
| yi* |
| xi* |
| x |
| { -q, p } |
| G |
| α* |
а соотношение (**) задает эффективную границу G. При изменении X* от нуля до бесконечности Y* также меняется от нуля до бесконечности.
Множитель Лагранжа в задаче (6.2)-(6.4) равен отношению прироста затрат к приросту выпуска на эффективной кривой, т.е. угол наклона касательной к эффективной кривой в точке (X*, Y*) (угол α* на рис.6.3), связан с множителем Лагранжа ν* соотношением
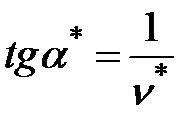 .
.
На основе формулы (*) для множителя Лагранжа в задаче (6.2)-(6.4) получаем
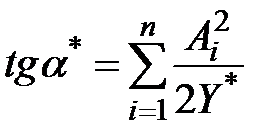 .
.
Таким образом, при изменении X* от нуля до бесконечности множитель Лагранжа растет от нуля до бесконечности, а угол α* изменяется от 900 до нуля.
Рассмотрим некоторую произвольную точку (X, Y), принадлежащую эффективной границе множества G. Решим задачу оптимизации (6.2)-(6.4) с Y=Y и найдем ее решение yi и xi  , а также множитель Лагранжа ν.
, а также множитель Лагранжа ν.
Очевидно, что 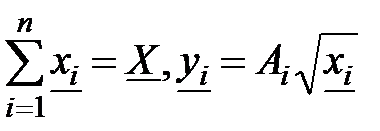 ,
,
Т.к. в противном случае точка (X, Y) не лежала бы на эффективной границе G. Как было показано выше, назначив цены p и q такими, что 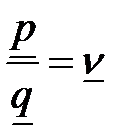 , мы сделаем план затрат и выпуска выгодным для каждого из предприятий. Таким образом, проблема выбора стимулирующего механизма с ценами на ресурсы и продукцию, одинаковыми для всех предприятий, может быть решена, если выбранные каким-то образом значения (X, Y) лежат на эффективной границе множества их достижимых значений. Можно показать, что это свойство сохраняется и для более сложных экономических систем.
, мы сделаем план затрат и выпуска выгодным для каждого из предприятий. Таким образом, проблема выбора стимулирующего механизма с ценами на ресурсы и продукцию, одинаковыми для всех предприятий, может быть решена, если выбранные каким-то образом значения (X, Y) лежат на эффективной границе множества их достижимых значений. Можно показать, что это свойство сохраняется и для более сложных экономических систем.
По принципиально подобной схеме могут рассматриваться модели экономического механизма с несколькими ресурсами. Известны также методы построения систем стимулирования на основе двойственных оценок задач линейного программирования.
Дата публикования: 2014-10-04; Прочитано: 1570 | Нарушение авторского права страницы | Мы поможем в написании вашей работы!
