Теорема Гаусса. Постулат Максвелла

Вначале рассмотрим понятие потока вектора через поверхность. Пусть в электростатическом поле есть некоторый элемент поверхности, площадь которого численно равна ds. Выберем положительное направление нормали (перпендикуляра) к элементу поверхности. Вектор в некотором масштабе (рис. 1.2) равен площади элемента ds, а его направление совпадает с положительным направлением нормали.

Будем полагать, что площадь элемента достаточно мала, чтобы в пределах этого элемента вектор 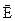можно было считать одним и тем же во всех точках. Тогда поток вектора 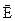через элемент поверхности определится скалярным произведением

Если поверхность S, через которую определяется поток вектора велика, то этот поток определяется с помощью интеграла по поверхности.

Теорема Гаусса формулируется следующим образом: поток вектора напряженности электрического поля сквозь замкнутую поверхность в однородном изотропном диэлектрике равен отношению электрического заряда, заключенного внутри этой поверхности, к диэлектрической проницаемости диэлектрика.

Математическое выражение теоремы Гаусса в интегральной форме имеет вид

. (1.9)

Для любой среды справедлива обобщенная теорема Гаусса или постулат Максвелла:

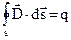. (1.10)

Теорема Гаусса и постулат Максвелла в дифференциальной форме записи имеют вид:

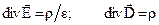
или в иной форме:

,

где r -объемная плотность электрического заряда в данной точке пространства. Выражение, стоящее в левой части уравнения, называется расхождением или дивергенцией вектора напряженности или электрического смещения.

Выражение для дивергенции в различных системах координат имеет различную форму записи. Так, в декартовой системе координат она имеет следующий вид:

,

здесь Е_х; Е_у; Е_z – проекции вектора 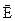на соответствующие оси координат.