Ориентированные и неориентированные сети

Дугу (i, j) называют направленной от узла i к узлу j, если дополнительный поток из i в j, протекающий по этой дуге, увеличивает величину уже существующего в ней потока, а противоположный дополнительный поток уменьшает эту величину. Направленные дуги иногда обозначают следующим образом: [ i, j ]. Направленная дуга называется ориентированной и в графическом представлении сети обозначается линией со стрелкой (см. рис. 2а). Дуга, не имеющая направления, называется неориентированной и в графическом представлении сети обозначается линией (см. рис. 2б).

Сети (графы)также могут быть ориентированными (содержащими ориентированные дуги - орграфами) и неориентированными (содержащими только неориентированные дуги).

Цепью [ i, j,..., k ] из узла i в узел k называют подграф G ₁ сети G, состоящий из последовательности дуг и узлов, в которой конечный узел каждой дуги (исключая узлы i и k) является начальным узлом следующей дуги. Цепь может включать неориентированные дуги.

Путем (i, j,..., k) из узла i в узел k называют подграф G ₂ сети G, состоящий из последовательности дуг и узлов, в которой каждый узел (исключая узлы i и k) является начальным или конечным узлом только двух дуг из G ₂ и каждая дуга пути начинается и заканчивается в узлах из G ₂.

Контур - конечная цепь с началом и концом в одном и том же узле.

Цикл - конечный путь с началом и концом в одном и том же узле.

Петля - цикл или контур из одной дуги и одного узла.

Не содержащие контуров сети (графы)называют бесконтурными, а не содержащие циклов - ациклическими.

Сеть (граф) связна, если для любых двух ее узлов существует соединяющий их путь.

Сеть сильно связна (граф полный), если для любых двух ее узлов существует соединяющая их цепь.

Граф G = G (V, E) называется двудольным, если V можно представить как объединение непересекающихся множеств, скажем V = A È B, так что каждое ребро имеет вид (v_i, v_j), где v_i Î A и v_j Î B. Двудольный граф называется полным двудольным графом K_{m , n}, если A содержит m вершин, B содержит n вершин и для каждого v_i Î A, v_j Î B имеем (v_i, v_j)Î E.

Пример Полный двудольный граф K _2,4 и полный граф K ₄.

Несвязный граф состоит из компонент связности. Компонента связности - множество вершин такое, что из любой вершины этого множества есть путь в любую другую вершину этого множества, но ни из какой вершины этого множества нельзя попасть в некоторую вершину вне этого множества. Очевидно, что сумма количеств вершин компонент связности равна количеству вершин графа. Заметим, что компонента связности может состоять из одной вершины. Если у графа n вершин, то он не может состоять из более чем n компонент связности. У связного графа компонента связности единственная.

У несвязного графа любая компонента связности состоит не более, чем из n-1 вершин. Если известно, что у графа k компонент связности, то даём ещё более строгую оценку: любая компонента связности состоит из не более, чем из n-k+1 вершин.

Если у несвязного графа k компонент связности, то для получения связного графа нужно добавить в граф как минимум k-1 ребро.

Псевдограф — граф, который может содержать петли и/или кратные рёбра

Мультиграф - граф, в котором может быть пара вершин, которая соединена более чем одним ребром (ненаправленным), либо более чем двумя дугами противоположных направлений.

Степенью вершины называется число ребер графа, которым принадлежит эта вершина.

Теорема о сумме степеней вершин графа: В графе G сумма степеней всех его вершин — число четное, равное удвоенному числу ребер графа. Формула суммы степеней для графа G =(V,E):

Следствие. Число нечетных вершин любого графа четно.

Свойства степени вершины:

· В графе G(V,E) сумма степеней всех его вершин – число четное, равное удвоенному числу ребер графа.

· Число нечетных вершин любого графа четно.

· Во всяком графе с n вершинами, где n ≥ 2 всегда найдутся, по меньшей мере, две вершины с одинаковыми степенями.

· Если в графе с n вершинами (n ≥ 2) в точности две вершины имеют одинаковую степень, то в этом графе всегда найдется либо в точности одна вершина степени 0, либо в точности одна вершина степени n-1.

Гамильтонов граф —это граф, содержащий гамильтонову цепь или гамильтонов цикл.

Гамильтонов путь (или гамильтонова цепь) — путь (цепь), содержащий каждую вершину графа ровно один раз. Гамильтонов путь, начальная и конечная вершины которого совпадают, называется гамильтоновым циклом. Гамильтонов цикл является простым остовным циклом.

Простой цикл —цикл, не проходящий дважды через одну вершину.

Остов - подграф, содержащий все вершины графа.

Цикломатическое число графа — минимальное число рёбер, которые надо удалить, чтобы граф стал ациклическим. Для связного графа существует соотношение: p ₁(G)= p ₀(G)+| E (G)|-| V (G)| где p ₁(G) — цикломатическое число, p ₀ — число компонент связности графа, | E (G)| — число рёбер, а | V (G)| — число вершин.

Эйлеров граф - граф, имеющий эйлеров цикл – замкнутую цепь, содержащую все вершины и все рёбра. Очевидно, что эйлеров граф должен быть связным. Если снять ограничения на замкнутость цепи, то граф называется полуэйлеровым.

Теорема (критерий эйлеровости):

Граф с более чем одной вершиной имеет эйлеров цикл тогда и только тогда, когда он связный и каждая его вершина имеет чётную степень.

Доказательство: Предположим, что граф G имеет эйлеров цикл. Граф является связным, так как каждая вершина принадлежит циклу. Для всякой вершины v графа G каждый раз, когда эйлеров цикл проходит через v, он вносит 2 в степень v. Поэтому степень v чётная.

Обратно, нужно показать, что каждый связный граф, у которого степени вершин чётные, имеет эйлеров цикл. Докажем эту теорему, используя индукцию по числу вершин. Поскольку теорема тривиально справедлива при n < 3, начнём индукцию с n=3. Предположим, что каждый связный граф, имеющий менее k вершин, и все вершины которого обладают чётной степенью, содержит эйлеров цикл. Пусть G – связный граф, содержащий k вершин, степени которых чётные. Допустим, что v ₁ и v ₂ - вершины графа G. Поскольку граф G – связный, существует путь из v ₁ в v ₂ .Поскольку степень v ₂ – чётная, существует неиспользованное ребро, по которому можно продолжить путь. Поскольку граф конечный, то путь, в конце концов, должен вернуться в v ₁ , и эйлеров цикл С₁ можно считать построенным. Если С₁ является эйлеровым циклом для G, тогда доказательство закончено. Если нет, то пусть G^/ - подграф графа G, полученный удалением всех рёбер, принадлежащих С₁. Поскольку С₁ содержит чётное число рёбер, инцидентных каждой вершине, каждая вершина подграфа G^/ имеет чётную степень.

Пусть e – ребро графа G^/ , пусть G_e – компонента графа G^/ , содержащая е. Поскольку G^/ имеет менее, чем k, вершин, и у каждой вершины графа G^/ чётная степень, граф G^/ имеет эйлеров цикл. Пусть С₂ . Далее у С₁ и С₂ имеется общая вершина, допустим, а. Теперь можно продолжить эйлеров цикл, начиная его в а, пройти С₁ , вернуться в а, затем пройти С₂ и вернуться в а. Если новый эйлеров цикл не является эйлеровым циклом для G, продолжаем использовать этот процесс, расширяя наш эйлеров цикл, пока, к конце концов, не получим эйлеров цикл для G .

На рис. 3 приведены примеры ориентированной и неориентированной (а), (е) сетей и содержащихся в них цепи (б) и контура (в); пути (б, д), цикла (в, е) и петли (г); бесконтурной (ж) и ациклической (з); связной (а, е, ж, з) и сильно связной (а, е) сетей.

Разрез C в графе - множество его дуг, исключение которых из сети G разделяет ее на два несвязных между собой подграфа G₁, G₂ исходной сети. То есть:

C = {(i, j): (i, j) A}:

G = G ₁ G ₂ C; G ₁Ç G ₂ = 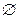, G ₁Ç C = 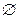, G ₂Ç C = 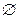; i, j G: i G ₁, j G ₂; (i, j) C.

Величина разреза C, его пропускная способность R_c (G ₁ G ₂ ) в направлении от G ₁ к G ₂- это сумма пропускных способностей r_ij всех дуг [ i, j ] разреза C, начинающихся в G ₁ и оканчивающихся в G ₂(см. рис. 4):

R_c (G ₁ G ₂ ) = r_ij.

Таким образом, каждый разрез ориентированной сети характеризуется двумя пропускными способностями: R_c (G ₁ G ₂ ) и R_c (G ₂ G ₁ ). В приложениях теории графов для сетей с одним источником s и одним стоком r большое значение имеют разрезы, разделяющие сток и исток, причем важной оказывается только величина разреза в направлении от источника к стоку. Для таких разрезов s G ₁, r G ₂; а R_c (s r) = R_c. В каждой конкретной сети разрезов этого типа может быть несколько. Тот из них, величина которого наименьшая, называется минимальным разрезом, а тот, величина которого наибольшая - максимальным разрезом.