Цифровые автоматы 1-го и 2-го рода, автоматы Мили и Мура

Автоматы 1-го и 2-го рода различаются законами функционирования.

Закон функционирования для ЦА 1-го рода включает в себя функции:

s(t) = d(s(t-1), x (t)),

y (t) = l(s(t-1), x (t)).

Видно, что характер зависимостей s(t) и y (t) от s(t-1) и x (t) является одинаковым, естественно, что операторы d и l являются различными.

Функция выхода ЦА 2-го рода отличается от такой функции ЦА 1-го рода тем, что используется состояние в данный момент времени s(t):

y (t) = l(s(t), x (t)).

Таким образом, закон функционирования ЦА 2-го рода есть:

s(t) = d(s(t-1), x (t)),

y (t) = l(s(t), x (t)).

Частный случай автомата 2-го рода - ЦА Мура. В том автомате функция выхода зависит только от данного состояния:

y(t) = l(s(t)).

Ясно, что зависимость от x (t) отсутствует только явно, на самом деле зависимость имеется (неявно). В том можно убедиться, подставив в функцию выхода данное состояние s(t) по функции перехода:

y (t) = l(d(s-1), x (t)) = l'(s(t-1), x (t)).

Получается некоторая новая функция выхода l'.

Нелишне ещё раз записать законы функционирования автоматов Мили и Мура, используя в качестве индексов "ми", "му":

ЦА Мили;

s(t)_ми= d(s(t-1), x (t)),

y (t)_ми=l(s(t-1), x (t)).

ЦА Мура.

s(t)_му= d(s(t-1), x (t)),

y (t)_му=l(s(t)).

У ЦА Мили выходной сигнал имеется только тогда, когда есть входной сигнал, а у ЦА Мура выходной сигнал имеется всегда. Целесообразно считать, что выходной сигнал у ЦА Мили носит импульсный характер, а у ЦА Мура - потенциальный характер.

y2

y1

Диаграммы работы ЦА Мили (рис.1,а) и Мура (рис.1,б) показаны на рис. Рис.5. ЦА Мили и Мура

Рис.6. Диаграмма работы ЦА Мили Рис.7. Диаграмма работы ЦА Мура

3. Автоматы, выполняющие роль "0" и

"1" в алгебре автоматов. С - автомат

Любая алгебра должна иметь конструкции, выполняющие в ней роль "0" и "1". По аналогии с алгеброй алгоритмов роль "0" выполняет пустой автомат (ноль-автомат), его следует обозначать с отступлением от принятых правил как ЦА0. Пустой автомат- это автомат, в котором запрещены всевозможные переходы. Естественно, что ЦАА \/ ЦА0 = ЦАА, ЦАА /\ ЦА0 = ЦА0.

Роль "1" возлагается на полный ЦА (ЦА1), в простейшем случае такой автомат представляет собой настраиваемое объединение рассматриваемых автоматов. Естественно, что ЦАА \/ ЦА1 = ЦА1, ЦАА /\ ЦА1 = ЦАА, дополнение ЦА1 = ЦА0, дополнение ЦА0 = ЦА1.

В данном вопросе следует затронуть ещё одно объединение, в котором одновременно реализуются автомат Мили и автомат Мура (рис.5). Как известно, первая функция автоматов Мили и Мура является одинаковой. Следовательно, в объединении она реализуется один раз. Что касается вторых функций, то они - разные и имеют свои логические схемы.

Закон функционирования С -автомата следует записать следующим образом:

s(t) = d(s(t-1), x (t)),

y (t)_ми= l(s(t-1), x (t));

y (t)_му= l(s(t)).

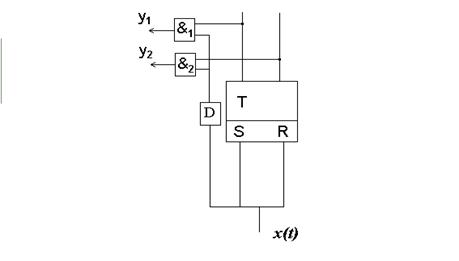
Рис.5. С – автомат

На рисунке 6 представлен структурный автомат С реализующий функции автомата Мили и Мура одновременно.