Дифференциальные уравнения движения Навье-Стокса

При движении реальной (вязкой) несжимаемой жидкости в потоке жидкости помимо сил давления и тяжести действуют также силы трения.

1. Действие сил трения T на выделенный в потоке вязкой жидкости элементарный параллелепипед проявляется в возникновении на его поверхности касательных напряжений τ.

2. Рассмотрим первоначально относительно простой случай одномерного плоского потока капельной жидкости в направлении оси x.

В этих условиях касательные напряжения возникают лишь на поверхности dF верхней и нижней граней элементарного параллелепипеда, причём

dF = dx^.dy.

Если касательное напряжение на нижней грани равно τ, то на верхней грани оно составляет

,

где производная - выражает изменение касательного напряжения вдоль оси z в точках, лежащих на нижней грани параллелепипеда; производная - представляет собой изменение этого напряжения вдоль всей длины dz ребра параллелепипеда.

3. Тогда проекция равнодействующей сил трения на ось x

.

Подставим в это выражение значение касательного напряжения τ, определённого ранее (закон внутреннего трения Ньютона) по уравнению

,

где μ – вязкость жидкости.

Тогда получим:

.

4. В более общем случае трёхмерного потока составляющая скорости W_x будет изменяться не только в направлении z, но и в направлении всех трёх осей координат.

Тогда проекция равнодействующей сил трения на ось x примет вид

.

Сумма вторых производных по осям координат называется оператором Лапласа - .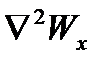

Следовательно, проекция равнодействующей сил трения на ось x может быть представлена как

.

Соответственно на ось y: ,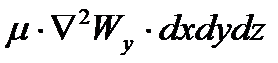

на ось z: .

5. Проекции на оси координат равнодействующей всех сил (тяжести и трения), быстродействующих на элементарный объём капельной жидкости (с учётом проекций сил тяжести и давления, полученных при выводе уравнений Эйлера), составляют:

на ось x ,

на ось y ,

на ось z .

6. Суммы проекций сил на оси координат, в соответствии с основным принципом динамики должны быть равны произведению массы жидкости, заключённой в элементарном объёме (), на проекции ускорения на оси координат.

Поэтому, приравнивая проекции равнодействующей произведения и массы на проекции ускорения после сокращения на dx^.dy^.dz, получим

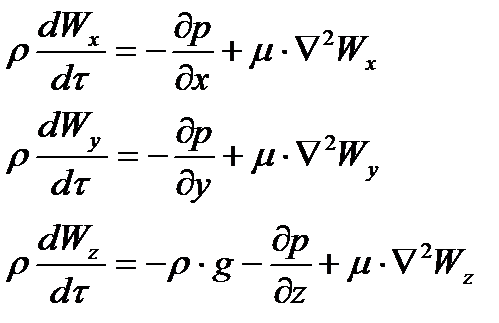(4)

(Уравнения Навье-Стокса, описывающие движение вязкой капельной жидкости), где соответствующие субстанциональные производные выражены для установившегося потока уравнением (2) стр. 2, а для неустановившегося потока уравнением (3) стр. 2.

7. При движении сжимаемой жидкости в ней дополнительно возникают вызванные трением силы растяжения и сжатия.

Уравнения Навье-Стокса в этом случае принимает вид:

(5)

Это масса единицы объёма ρ на проекцию её ускорения, то есть представляет собой проекцию равнодействующей сил инерции, возникающих в движущейся жидкости.	Отражают влияние сил тяжести.	Частичные производные отражают влияние изменения гидростатического давления.	Произведение вязкости на сумму вторых производных проекций скорости; отражают влияние сил трения на движущуюся жидкость.	Частичные производные выражают изменение скорости по осям x, y, z, связанные с действием сил сжатия и растяжения, причём

Каждый член уравнения имеет размерность соответствующей силы (тяжести, давления, трения и инерции), отнесённой к единице объёма жидкости.

8. При движении идеальной жидкости, когда силы трения отсутствуют, при подстановке μ = 0 в уравнения (4) последние совпадают с уравнением (1), то есть уравнения движения Эйлера можно получить как частный случай уравнений Навье-Стокса.

9. Полное описание движения вязкой жидкости в его наиболее общей форме возможно путём решения уравнений Навье-Стокса совместно с уравнением неразрывности потока. Однако уравнения Навье-Стокса не могут быть решены в общем виде. Получены решения этой сложной системы уравнений только для некоторых частных случаев.

В большинстве наиболее важных для промышленной практики случаев применения уравнений Навье-Стокса становится возможным либо при ряде упрощающих допущений, либо при преобразовании этих уравнений методами теории подобия.