 |
Главная Случайная страница Контакты | Мы поможем в написании вашей работы! | |
Глава 7. Задачи и упражнения
|
|
7.1. ПОВТОРЕНИЕ МАТЕРИАЛА ИЗ КУРСА
«ДИСКРЕТНАЯ МАТЕМАТИКА»
Совершенной конъюнктивной нормальной формой (СКНФ) логической функции  называют представление её в виде конъюнкции макстермов, построенных из аргументов рассматриваемой функции:
называют представление её в виде конъюнкции макстермов, построенных из аргументов рассматриваемой функции:
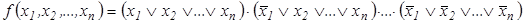 .
.
Совершенной дизъюнктивной нормальной формой (СДНФ) логической функции  называют представление её в виде дизъюнкции минтермов, построенных из аргументов
называют представление её в виде дизъюнкции минтермов, построенных из аргументов  :
:
 .
.
Пример. Привести заданную логическую функцию к форме СДНФ с использованием обоих известных способов:

| x | y | z | 
| 
| 
| 
|

Пример. Привести заданную логическую функцию к форме СКНФ с использованием обоих известных способов:
| x | y | z | 
| 
| 
| f(x, y, z) |


1. Построить таблицы истинности для заданной логической функции:
а)  ;
;
б)  ;
;
в)  ;
;
г)  .
.
2. Привести заданную логическую функцию к форме СДНФ, используя табличный способ и способ эквивалентных преобразований:
а)  ;
;
б)  ;
;
в)  ;
;
г)  .
.
3. Привести заданную логическую функцию к форме СКНФ, используя табличный способ и способ эквивалентных преобразований:
а)  ;
;
б)  ;
;
в)  ;
;
г)  .
.
7.2. ЛОГИКА ВЫСКАЗЫВАНИЙ
1. Определить, какие из приведенных выражений являются формулами исчисления высказываний:
1)  ;
;
2)  ;
;
3) 
4)  ;
;
5) 
6) 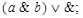
7) 
8) (
9)  .
.
Пример. Пусть задана формула 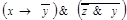 , выписать все подформулы заданной формулы с распределением их по уровням вложенности используя табличное представление (а) и представление в виде дерева (б).
, выписать все подформулы заданной формулы с распределением их по уровням вложенности используя табличное представление (а) и представление в виде дерева (б).
а)
| Подформула | Глубина |
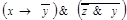
| |

| |

| |

| |

|

2. Выписать все подформулы заданных формул с распределением их по уровням вложенности, используя табличное представление и представление в виде дерева:
1)  ;
;
2)  ;
;
3)  ;
;
4)  ;
;
5)  ;
;
6)  ;
;
7)  ;
;
8)  ;
;
9)  ;
;
10)  ;
;
11)  ;
;
12)  ;
;
13)  .
.
3. Доказать, используя метод эквивалентных преобразований, справедливость аксиом исчисления высказываний:
1)  ;
;
2)  ;
;
3)  ;
;
4)  ;
;
5)  .
.
Пример. Используя алгоритм редукции, доказать общезначимость следующей формулы:  .
.
Пусть при некоторой интерпретации  .
.
Это возможно, только если
 ; ;
| (7.1) |
 . .
| (7.2) |
  ; ;
|
  ; ;
|
  . .
|
 , это означает, что возможны следующие значения c и a:
, это означает, что возможны следующие значения c и a:
  ; ;
|
  ; ;
|
  . .
|
 имеем
имеем  . Это единственно допустимые для c и b значения, при которых формула принимает значение «ложь». Сопоставляем полученные результаты с ранее рассмотренными возможными значениями переменных.
. Это единственно допустимые для c и b значения, при которых формула принимает значение «ложь». Сопоставляем полученные результаты с ранее рассмотренными возможными значениями переменных.
Оказывается, что при  единственное допустимое значение для a - это
единственное допустимое значение для a - это  , а при
, а при  единственное допустимое значение
единственное допустимое значение  . То есть переменная a должна принимать взаимно исключающие значения, что невозможно. Следовательно, предположение о существовании интерпретации, при которой формула
. То есть переменная a должна принимать взаимно исключающие значения, что невозможно. Следовательно, предположение о существовании интерпретации, при которой формула  принимает значение «ложь», неверно, и это означает ее общезначимость.
принимает значение «ложь», неверно, и это означает ее общезначимость.
4. Доказать, используя алгоритм редукции:
1) 
2) 
3) 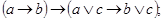
4) 
5) 
6) 
7) 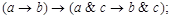
8) 
9)  ;
;
10)  ;
;
11) 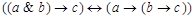 ;
;
12) 
5. Используя правила эквивалентных преобразования, доказать тождественную истинность выражений из п. 4.
Пример. Доказать, используя метод резолюций, что S является логическим следствием множества гипотез H, где  , а
, а  . Сначала преобразуем множество гипотез в множество дизъюнктов:
. Сначала преобразуем множество гипотез в множество дизъюнктов:
1.  ;
;
2.  ;
;
3.  ;
;
4.  .
.
Для доказательства того, что H |= S, необходимо и достаточно доказать невыполнимость следующего множества дизъюнктов:
 .
.
1.  2.
2.  3.
3.  4.
4. 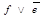 5. a
6. b
7.
5. a
6. b
7.  8. d (
8. d (  )
9. )
9.  ( (  )
10. c ( )
10. c (  )
11. )
11. 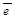 ( (  )
12. )
12.  ( (  )
13. )
13.  ( ( )
14. Пустой дизъюнкт ( )
14. Пустой дизъюнкт (  ) )
|
1) H = {a®(  Úc), c&d®e,
Úc), c&d®e,  ®d&
®d&  }, S = a®(b®f);
}, S = a®(b®f);
2) H = {(aÚb)®c&d, (dÚe)®f}, S = a®f;
3) H = {a®b&c,  Úd, (e®
Úd, (e®  )®
)®  , b®a&
, b®a&  }, S = b®e;
}, S = b®e;
4) H = {(a®b)&(c®d), (b®e)&(d®f), e&f, a®c}, S =  ;
;
5) H = {pÚ  Ú
Ú  , q, r, tÚ
, q, r, tÚ 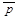 Ú
Ú  , tÚ
, tÚ 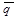 }, S = p&q&r;
}, S = p&q&r;
6) H = {a~b, b®c,  Úd,
Úd,  ®d}, S = d;
®d}, S = d;
7) H = {(aÚb)®(cÚd),  , d®g}, S = c;
, d®g}, S = c;
8) H = {(c®g)&(d®s), s&g®e,  }, S =
}, S =  Ú
Ú  ;
;
9) H = {abÚ  ,
,  Úc, c®d, aÚd}, S = d;
Úc, c®d, aÚd}, S = d;
10) H = {a&  ,
,  Úg,
Úg,  Ú(cÚd)}, S = c;
Ú(cÚd)}, S = c;
11) H = {  Ú
Ú  Úb, d®a,
Úb, d®a,  Úb}, S =
Úb}, S =  ;
;
12) H = {  Ú(b®c),
Ú(b®c),  Úe, fÚ(
Úe, fÚ(  )}, S =
)}, S =  Ú
Ú  Úf;
Úf;
13) H = {(  Úb)&(
Úb)&(  Úd), (
Úd), (  Úe)&(
Úe)&(  Úf),
Úf),  Ú
Ú  ,
,  Úc}, S =
Úc}, S =  .
.
Пример. Используя метод прямой и обратной дедукции доказать справедливость вывода для заданного множества гипотез Н={h1, h2 ,..., hm} и следствия S:
 ,
, 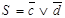 .
.
При доказательстве на основе прямой дедукции доказывается справедливость следующей формулы:  , а при обратной дедукции следующей:
, а при обратной дедукции следующей:  . При построении доказательства по дедукции в качестве механизма воспользуемся методом эквивалентных преобразований.
. При построении доказательства по дедукции в качестве механизма воспользуемся методом эквивалентных преобразований.
Прямая дедукция:  .
.
Доказательство:

Обратная дедукция: 
Доказательство:

Дата публикования: 2014-10-29; Прочитано: 1652 | Нарушение авторского права страницы | Мы поможем в написании вашей работы!
