Недетерминированные алгоритмы

Мы собираемся более подробно классифицировать задачи, не попадающие ни в класс P, ни в класс E. Для этого вводится понятие недетерминированного алгоритма [26, стр. 443].

Неформально, мы определяем состояние алгоритма как комбинацию адреса выполняемой в текущий момент команды и значений всех переменных. Все алгоритмы, рассматривавшиеся до сих пор были детерминированными; иначе говоря, во всех них для любого данного состояния существует не больше одного вполне определенного "следующего" состояния. Другими словами, детерминированный алгоритм в каждый момент времени может делать только что-либо одно. В недерминированном алгоритме для любого данного состояния может быть больше одного допустимого следующего состояния; другими словами, недетерминированный алгоритм в каждый момент времени может делать больше одной вещи. Недетерминированные алгоритмы не являются в каком-то смысле вероятностными или случайными алгоритмами; они являются алгоритмами, которые могут находиться одновременно во многих состояниях.

Недетерминированность лучше всего понять, рассматривая алгоритм, который производит вычисления до тех пор, пока не доходит до места, в котором должен быть сделан выбор из нескольких альтернатив. Детерминированный алгоритм исследовал бы одну альтернативу, а потом бы возвращался бы для исследования другой альтернативы. Недетерминированный алгоритм может исследовать все возможности одновременно, "копируя", в сущности, самого себя для каждой альтернативы. Все копии работают независимо, не сообщаясь друг с другом каким-либо образом. Эти копии, конечно, могут создавать дальнейшие копии и т. д. Если копия обнаруживает, что она сделала неправильный (или безрезультатный) выбор, она прекращает выполняться. Если копия находит решение, она объявляет о своем успехе, и все копии прекращают работать.

Недетерминированный алгоритм можно моделировать с помощью недетерминированной машины Тьюринга. Машина Тьюринга, которая была введена в §4, является очевидно детерминированной. Обобщим данное там определение, допустив, что каждое значение функции M является множеством троек {<записываемый символ>, <переход>, <номер инструкции>}. Теперь для каждого состояния машины может быть несколько следующих состояний, в соответствии с функцией перехода. И в каждом следующем состоянии запускается новая копия данной машины Тьюринга. Формальное определение недетерминированной машины Тьюринга см. в [6].

Очевидно, никакое физическое устройство не способно на неограниченное недетерминированное поведение; недетерминированные алгоритмы - это абстракция, которая позволяет нам игнорировать некоторые проблемы программирования поиска с возвращением.

Определим NP как класс всех задач, которые можно решить недетерминированными алгоритмами, работающими в течение полиномиального времени, т. е. недетерминированными алгоритмами, в которых всегда есть путь успешного вычисления за время, полиномиальное относительно входа; очевидно, P Í NP. Поскольку путей вычисления может быть экспоненциально много, вероятно, что алгоритмы, допустимые в этом случае, намного сильнее, чем детерминированные алгоритмы, допустимые для задач из P.

Укажем причины, по которым задача коммивояжера попадает в класс NP. С оптимизационными проблемами (такими, например, как задача коммивояжера) связаны соответствующие проблемы распознавания свойств. Такие задачи имеют только два возможных решения - "да" или "нет". Выражаясь абстрактно, проблема распознавания T состоит просто из двух множеств: множества D_T всех возможных частных случаев (индивидуальных задач) и множества Y_T (Y_T ÌD_T) частных случаев с ответом "да".

Задача распознавания, соответствующая задаче о коммивояжере, может быть сформулирована следующим образом.

Условие. Заданы конечное множество C = {c₁, c₂,..., c_m} "городов", "расстояние" d(c_i, c_j) между каждой парой городов c_i, c_j из C и граница B - положительное число.

Вопрос. Существует ли "маршрут", проходящий через все города из C, длина которого не превосходит B? Другими словами, существует ли последовательность <c_k(1), c_k(2),..., c_k(m)> элементов C такая, что

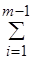d(c_k(i), c_k(i+1))+d(c_k(m), c_k(1)) £ B?

Относительно соответствия между задачами распознавания и задачами оптимизации важно отметить, что задача распознавания не может быть сложней соответствующей задачи оптимизации. Если для задачи о коммивояжере можно за полиномиальное время найти маршрут минимальной длины, то совершенно ясно как за полиномиальное время решить соответствующую задачу распознавания. Для этого только нужно найти маршрут минимальной длины, вычислить его длину и сравнить с заданной границей B.

Полиномиальный алгоритм задачи коммивояжера неизвестен. Предположим, однако, что имеется некоторый маршрут между городами, претендующий на решение задачи распознавания. Нетрудно проверить, является ли этот маршрут полным обходом всех городов, а если это так, то вычислить его длину, сравнить с границей B и тем самым выяснить является ли этот маршрут положительным решением задачи распознавания. Более того, эту "процедуру проверки" можно представить в виде алгоритма, временная сложность которого ограничена в виде полинома от | I |.

Недетерминированный алгоритм, во многих случаях, можно применить для решения задачи распознавания. Такой алгоритм состоит из двух различных стадий - стадии угадывания и стадии проверки. По заданному частному случаю I проблемы T на первой стадии происходит просто угадывание (генерация) некоторой структуры S. Мы можем считать, что для решения задачи запускается одновременно столько копий алгоритма, сколько существует различных структур S. Затем в каждой копии I и S вместе подаются в качестве входа на стадию проверки, которая выполняется обычным детерминированным образом и либо заканчивается ответом "да", либо заканчиваются ответом "нет", либо продолжается бесконечно без остановки (два последних случая можно не различать). Недетерминированный алгоритм "решает" проблему распознавания T, если для каждого частного случая I Î D_T выполнены следующие два свойства:

1. Если I ÎY_T, то существует такая структура S, угадывание которой для входа I приведет к тому, что стадия проверки, начиная работу на входе (I, S), закончится ответом "да".

2. Если I Ï Y_T, то не существует такой структуры S, угадывание которой для входа I обеспечило бы окончание стадии проверки на входе (I, S) ответом "да".

Например, недетерминированный алгоритм решения задачи о коммивояжере можно было бы построить, используя в качестве стадии угадывания просто выбор произвольной последовательности городов, а в качестве стадии проверки упомянутую выше "полиномиальную" процедуру" проверки маршрута. Очевидно, что для любого частного случая I найдется такая догадка S, что результатом работы стадии проверки на входе (I, S) будет "да" в том и только том случае, если для частного случая I существует маршрут искомой длины.