Координаты вектора относительно данного базиса

Рассмотрим конечномерное векторное пространство V размерности n, векторы e ₁, e ₂, …, e_n образуют его базис. Пусть a – произвольный вектор пространства V, тогда вектор линейно выражается через векторы базиса, a = a₁ e ₁ + a₂ e ₂ + … + a _ne_n.

Теорема 8.8. Разложение вектора a по векторам базиса производится единственным образом.

Доказательство. Предположим, что вектор a можно разложить по векторам базиса двумя способами:

a = a₁ e ₁ + a₂ e ₂ + … + a _ne_n.

a = a'₁ e ₁ + a'₂ e ₂ + … + a' _ne_n.

После вычитания из одного равенства другого, получим

(a₁ – a'₁) e ₁ + (a₂ – a'₂) e ₂ + … + (a _n – a' _n) e_n = 0,

из чего в силу линейной независимости базисных векторов e ₁, e ₂, …, e_n следует, что a₁ – a'₁ = 0, a₂ – a'₂ = 0, …, a _n – a' _n = 0, а затем что a₁ = a'₁, a₂ = a'₂, …, a _n = a' _n. Таким образом, коэффициенты разложения определяются однозначно. Теорема доказана.

Определение 8.13. Координатами вектора a относительно базиса e ₁, e ₂, …, e_n называются коэффициенты разложения вектора a по базисным векторам.

Координаты вектора принято записывать или в виде строки координат (координатной строки) – (a₁, a₂, …, a _n), или в виде координатного столбца: [ a ] = .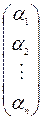

Пример 8.7. 1) В пространстве R ^2´2 вектор A = 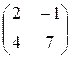раскладывается по векторам базиса Е ₁, Е ₂, Е ₃, Е ₄ следующим образом: А = 2 Е ₁ – Е ₂ + 4 Е ₃ + 7 Е ₄, следовательно, координатная строка этого вектора равна (2, –1, 4, 7).

2) В пространстве выбран базис а ₁ = (1, 3, –1), а ₂ = (–2, 1, 1),
а ₃ = (2, –2, –1). Найти координаты вектора a = (3, 0, –2) относительно базиса а ₁, а ₂, а ₃. Векторное равенство a = x ₁ а ₁ + x ₂ а ₂ + x ₃ а ₃ перепишем в виде системы линейных уравнений 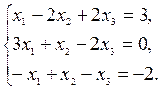Решая эту систему, получим x ₁ = 1, x ₂ = 1, x ₃ = 2, следовательно, координатная строка вектора a равна (1, 1, 2).

Каждому вектору a из произвольного векторного пространства V, в котором задан базис e ₁, e ₂, …, e_n, сопоставляется строка (или столбец) координат (a₁, a₂, …, a _n), причем единственным образом. Если V пространство размерности n, то строка координат принадлежит пространству Rⁿ, то есть возникает отображение: V ® Rⁿ. Обратно, по строке координат (a₁, a₂, …, a _n), (по вектору из Rⁿ) единственным образом можно построить вектор a = a₁ e ₁ + a₂ e ₂+ … + a _ne_n. Для этого отображения верна следующая теорема.

Теорема 8.9. Если векторы а ₁, а ₂, …, а_m из произвольного пространства V образуют линейно независимую систему векторов, то их строки (или столбцы) координат тоже линейно независимы.