Анализ решений задач линейного программирования

Рассмотрим следующую задачу ЛП:

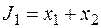
	(1)
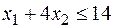
	(2)
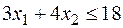
	(3)
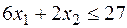
	(4)
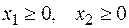
	(5)

Решением этой задачи являются следующие значения переменных 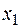и 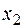(см. рис. 2.6.1):

.

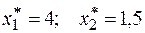а)

б)

Показатель качества (1) в рассматриваемой задаче ЛП характеризует суммарный выпуск продукции вида П1 и П2.

Найдем оптимальные решения еще для четырех целевых функций:

максимизации выпуска продукции П2

;

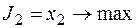максимизации выпуска продукции П1

;

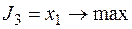максимизации прибыли

,

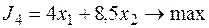где коэффициенты перед 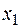и 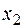взяты из таблицы исходных данных (см. табл. 2.6.1);

минимизации используемых ресурсов

,

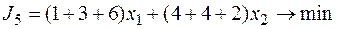т.е. .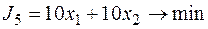

Таблица 2.6.1.

Характеристика	Вид продукции	Располагаемый ресурс
П1	П2
Резервы:
трудовые
материальные
финансовые
Выпуск			—
Прибыль		8,5	—
План			—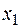

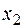
Для каждой приведенной целевой функции аналогично тому, как это делалось для 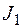, можно построить линию целевой функции и определить вершину в которой целевая функция будет иметь оптимальное значение. Результаты решения задачи по пяти целевым функциям сведены в табл. 2.6.2, из анализа которой можно сделать следующий вывод: координаты каждой вершины могут быть оптимальным решением задачи в некотором принятом смысле. Так, вершина С дает максимальный суммарный выпуск, вершины А — максимальный выпуск продукции П2 и т.д.

Таблица 2.6.2.

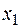
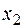
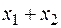
Целевая функция	Вершина				Прибыль	Используемый ресурс
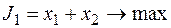
	С		1,5	5,5	28,75
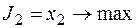
	A		3,5	3,5	29,75
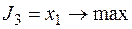
	D	4,5		4,5
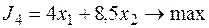
	B				33,5
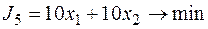
	F

Если перед нами стоит задача минимизировать используемые ресурсы, то очевидно, что при отсутствии требований на заданную номенклатуру ничего не надо выпускать.

Пользоваться таблицами типа 2.6.2 при анализе различных вариантов планов, несомненно, полезно. При этом окончательный выбор варианта оптимального плана должен делать не специалист по математическим методам, а руководитель, т.е. лицо, принимающее решение.

Рассмотрим далее, как влияет на оптимальное решение введение дополнительных ограничений. Пусть дана задача, которая графически представлена на рис. 2.6.2, а. Принимаем, что при максимизации оптимальное решение находится в вершине А и имеет значения 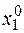, , 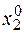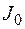. Рассмотрим, как влияют на оптимальное решение дополнительные ограничения, например, применительно к .

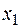Таблица 2.6.3.

См. рис. 2.6.2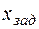
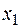
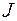
б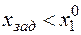
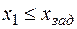
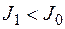
в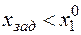
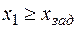
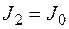
г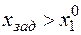
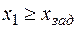
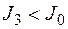
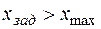
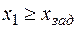
д			Нет

Из рис. 2.6.2 и данных табл. 2.6.3 видно следующее: дополнительное ограничение ухудшило целевую функцию (рис. 2.6.2, б); оптимальное решение не изменилось (рис. 2.6.2, в); оптимальное решение ухудшилось (рис. 2.6.2, г); характерно появление несовместности (рис. 2.6.2, д), которое привело к тому, что задача вообще не имеет решения.

Выводы:

1. Если оптимальным решением являются координаты вершины ОДР, то это значит, что сколько вершин имеет ОДР, столько оптимальных решений может иметь задача.

2. Поскольку чем больше ограничений, тем больше вершин, то, следовательно, чем больше ограничений, тем больше оптимальных решений.

3. Дополнительные ограничения в задачах ЛП не улучшаются ранее полученных оптимальных решений.

2.7. Содержательная и формальная постановка
транспортной задачи.

Транспортная модель является частным случаем общей сетевой модели оптимизации, интерес к которым связан с тем, что в рамках терминологии сетевых (графовых) моделей описываются многие задачи принятия решений, связанные с управлением системами различной природы. Особенности математической структуры сетевых моделей позволяют строить эффективные вычислительные алгоритмы решения таких задач, и именно этот фактор позволяет выделить транспортные задачи в самостоятельный класс специальных задач, изучение которых имеет важные практические приложения в различных областях деятельности.

Представим транспортную модель в следующем виде. Имеется:

- множество поставщиков A = {A_i, i = 1,…, m};

- множество потребителей B = {B_j, j = 1,…, n}.

Каждому поставщику соответствует объем имеющегося у него ресурса a_i, а каждому потребителю сопоставляется объем необходимого для него ресурса b_j. Предполагается, что каждый поставщик соединен с каждым потребителем, т.е. множество дуг такой сети E = A ´ B. Задана функция c: E ® R¹, характеризующая некоторое качество (время, стоимость, и т.п.) перевозки по дуге
e_ij = (A_i, B_j) Î E

В этом случае математической конструкцией, описывающей решение, может являться вектор

x = (x₁₁, x₁₂,....,x_1n, x₂₁,....,x_2n,...., x_mn)^т = ║x_ij║,

компоненты которого x_ij характеризуют объем перевозок от поставщика A_i к потребителю B_j. Ограничения накладываются на объем продукции, вывозимой от i -го поставщика, и количество продукции, которую необходимо завести
j -му потребителю. Целевая функция характеризует суммарные расходы на все такие перевозки.

Тогда математическая модель классической транспортной задачи имеет вид:

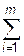
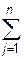c_ij x_ij ® min (1)

при ограничениях

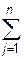x_ij £ a_i, i = 1,…, m, (2)

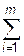x_ij ³ b_j, j = 1,…, n, (3)

x_ij ³ 0, i = 1,…, m, j = 1,…,n. (4)

В ситуациях, когда имеется равенство суммарного ресурса у всех поставщиков и суммарных потребностей всех потребителей,

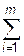a_i = 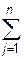b_j, (5)

неравенства в ограничениях транспортной модели приобретают вид равенств.

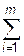
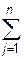c_ij x_ij ® min (6)

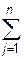x_ij = a_i, i = 1,…, m, (7)

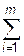x_ij = b_i, j = 1,…, n, (8)

x_ij ³ 0, i = 1,…, m, j = 1,…,n. (9)

Такая задача называется стандартной (закрытой) транспортной задачей. Следует отметить, что произвольная транспортная задача может быть сведена к стандартной путем введения фиктивных поставщиков (потребителей), объем ресурсов (потребностей) которых равен разности левой и правой части в ограничениях (2) (или (3)).

Транспортная задача (6)–(9) описывается линейными ограничениями и линейной целевой функцией, следовательно, для ее решения могут использоваться стандартные методы линейного программирования (симплекс-метод, например). Размерность такой задачи равна (m+n)´(mn). Однако для решения транспортных задач был разработан специализированный алгоритм (метод потенциалов), учитывающий особенности данной задачи. Рассмотрим, в чем состоят эти особенности.

2.8. Содержательная и формальная постановка
задачи о назначениях.

Частным случаем классической транспортной задачи (1)–(4) раздела 2.7 является задача о назначениях, которая помимо того, что сама имеет важное прикладное значение, часто используется, как вспомогательная при решении дискретных оптимизационных задач различного рода. Практическая суть задачи, из которой и возникло ее название, заключается в том, что имеется (n) должностей, на которые могут быть назначены (n) кандидатов, причем назначение некоторого i –го кандидата на j -ю должность связано с расходами равными c_ij. Необходимо так распределить кандидатов на должности, чтобы суммарные расходы были минимальны.

В этих условиях решение (распределение кандидатов) можно описать вектором x с компонентами x_ij, которые принимают значение 1 или 0 в зависимости от того, назначается i –ый кандидат на j –ю должность, или нет. Математическая модель такой задачи имеет вид

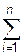
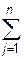c_ij x_ij ® min (1)

при ограничениях

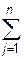x_ij = 1, i = 1,…, n, (2)

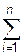x_ij = 1, j = 1,…, n, (3)

x_ij Î {0, 1}, i = 1,…, n, j = 1,…,n. (4)

Такая задача относится к классу задач линейного дискретного (целочисленного, булевого) программирования. В силу абсолютной унимодулярности матрицы условий такой задачи многогранник условий имеет только целочисленные вершины, поэтому решение такой задачи может быть получено на основе симплекс-метода. Так как задача о назначениях является частным случаем транспортной задачи, то она может быть решена и с использованием метода потенциалов.

Раздел 3. ПОСТАНОВКА И МЕТОДЫ РЕШЕНИЯ ДЕТЕРМИНРОВАННЫХ ЗАДАЧ ВЫБОРА С НЕЛИНЕЙНОЙ ЦЕЛЕВОЙ ФУКНЦИЕЙ И НЕЛИНЕЙНЫМИ ОГРАНИЧЕНИЯМИ

3.1. Особенности задач выбора с нелинейной целевой функцией и нелинейными ограничениями (задач нелинейного
программирования (НЛП))

В задачах ЛП полагалось, что себестоимость, цена и другие показатели, оценивающие эффективность организации производства не зависят от объема производства (вектор 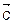не зависит от 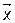). Однако, в общем случае, это не так. Так, например, на практике себестоимость единицы продукции снижается при увеличении объема производства (вектор 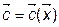). Для учета данных ситуаций вводят новый класс моделей исследования операций.

Определение 1. Задача выбора, в которой зависимости между переменными в целевой функции и/или в ограничениях являются нелинейными, называется задачей нелинейного программирования.

В общем случае задача нелинейного (математического) программирования имеет следующий вид:

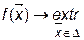
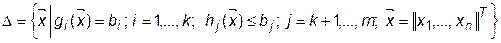
В зависимости от свойств, которыми обладают функции 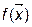, , 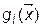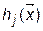различают следующие классы задач нелинейного программирования:

Определение 2. Множество (область) 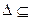R ⁿ называется выпуклым, если с каждыми двумя точками (альтернативам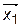и) и 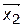, ему принадлежащими, оно включает весь отрезок, соединяющий данные точки, т. е. выполняется соотношение

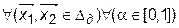
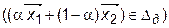
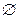— выпуклое по определению.

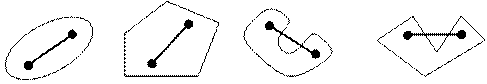
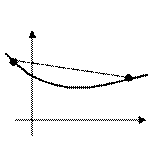
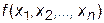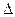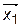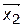Определение 3. Функция , заданная на выпуклом множестве , называется выпуклой, если для любых двух точек и из 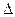и любого 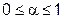выполняется соотношение

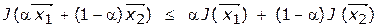
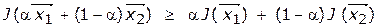
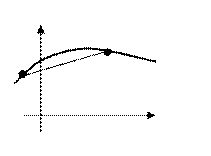
Согласно определению признака экстремума функция f(x) имеет максимум (минимум) в точке х*, если в достаточной близости от этой точки всем значениям х соответствуют значения f(x) меньшие (большие), чем f(x*). Для случая максимума это показано на рис. 3.1.1.

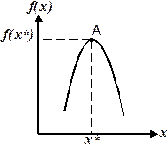Рис. 3.1.1

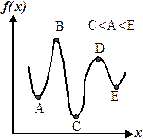
Рис. 3.1.2

Максимум и минимум функции объединяются понятием экстремум, который может быть как локальным, так и глобальным. На рис. 3.1.2 функция f(x) принимает максимальные значения в вершинах В и D. При этом B > D. В таком случае говорят, что точка В является глобальным максимумом, а точка D — локальным. Аналогично функция f(x) принимает минимальные значения в точках А, С, Е, причем С < A < E. В этом случае С будет глобальным минимумом, а А и Е — локальными минимумами. Из приведенных примеров видно, что глобальным максимумом (минимумом) называют такой максимум (минимум), который больше (меньше) всех остальных.

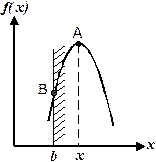Рис. 3.1.3

Достаточно часто при введении граничных условий типа х £ b, показанных на рис. 3.1.3, наибольшее значение функции находится на границе в точке х = b. При этом величина f(b) не удовлетворяет приведенному выше признаку экстремума.

В таких случаях говорят, что в точке х = b находится оптимум функции f(b) = B.

Наибольшее или наименьшее значение функции без учета того, где находится такое значение, — внутри заданного интервала или на его границе — называют оптимумом. Оптимум — более широкое понятие, чем экстремум. Если экстремум есть не у всех функций, то в практических задачах оптимум, как правило, есть всегда. Так же как и экстремумы, оптимумы могут быть локальными и глобальными.

Существующие методы дают возможность находить только локальные оптимумы. Если же есть подозрение, что в заданном интервале а_j £ x_j £ b_j целевая функция f(x_j) может иметь несколько оптимумов, то этот интервал следует разбить на n интервалов, в каждом интервале определить свои локальные оптимумы, а затем из всех локальных оптимумов выбрать глобальный. В таком случае задача нахождения глобального оптимума сводится к решению ряда задач, в которых ищется локальный оптимум.

В дальнейшем мы будем рассматривать нахождение только локального оптимума. Следует отметить, что в подавляющем большинстве практических экономических и технических задач оптимизации существует только один оптимум. Задачи нелинейной оптимизации с точки зрения методов решения делятся на два класса:

r задачи безусловной оптимизации;

r задачи условной оптимизации.

Особенности задач НЛП:

1. По сравнению с рассмотренными ранее задачами линейного программирования, в которых оптимальное решение соответствует некоторым крайним точкам (вершинам) выпуклого многогранника, в задачах нелинейного программирования оптимальное решение может соответствовать произвольной точке области D. В этих задачах решение может находиться как в точке, расположенной на границе допустимой области, так и в точке, расположенной внутри области, что определяется свойствами целевой и ограничивающих функций.

2. Многосвязность допустимой области и многоэкстремальность задачи. В задачах нелинейного программирования при произвольных ограничениях множество допустимых решений D может быть многосвязным, т.е. представлять собой объединение непересекающихся подмножеств. Решение в каждой такой области следует искать независимо от других, и выбирать из них наилучшее, однако установление факта многосвязности D, как правило, достаточно трудоемко.

Нахождение оптимума произвольной функции в допустимой области D, даже если она задается линейными ограничениями, равно как и нахождение оптимума даже линейной функции на невыпуклом множестве D, может привести к тому, что в исходной оптимизационной задаче будет существовать несколько локальных экстремумов, т.е. другими словами такая задача будет многоэкстремальна. Существуют значительные трудности в определении локальных экстремумов, число которых в общем случае может быть достаточно велико.

3. Так как целевая функция и множество допустимых альтернатив в задачах нелинейного программирования описываются произвольными нелинейными функциями, в ряде приложений эти функции могут быть разрывными или недифференцируемыми. Это создает дополнительные трудности в решении таких задач и требует разработки специфических методов нахождения оптимальных решений.