Экономических объектов 2 страница

Пример 2.2.2: фирма управляется двумя менеджерами. Предположим, что при работе двух менеджеров отрицательные эффекты происходят с вероятностью q ₁₂, 1-го менеджера – с вероятность q ₁, 2-го менеджера – с вероятность q ₂, при отсутствии менеджеров – с вероятностью q ₀. Пусть 1-ый менеджер имеет частоту принятия верных решений по парированию отрицательных эффектов p ₁, 2-ой ‑ p ₂. Все отрицательные эффекты независимы друг от друга. Найти вероятность парирования отрицательных эффектов в фирме.

Решение: рассмотрим гипотезы

Г ₁₂ ‑ работают оба менеджера;

Г ₁ ‑ работает лишь 1-ый менеджер;

Г ₂‑ работает лишь 2-ой менеджер;

Г ₀‑ ни один из менеджеров не работает.

Введем событие A, как парирование отрицательных эффектов в фирме. Тогда

Pr (Г ₁₂) = p ₁ p ₂; Pr (A ú Г ₁₂) = 1 - q ₁₂;

Pr (Г ₁) = p ₁ (1- p ₂); Pr (A ú Г ₁) = 1 - q ₁;

Pr (Г ₂) = p ₂ (1- p ₁); Pr (A ú Г ₂) = 1 - q ₂;

Pr (Г ₀) = (1- p ₁) (1- p ₂); Pr (A ú Г ₀) = 1 – q ₀.

Используя формулу (2.2.3), получим

Pr (A) = Pr (Г ₁₂) Pr (A ú Г ₁₂) + Pr (Г ₁) Pr (A ú Г ₁) +

+ Pr (Г ₂) Pr (A ú Г ₂) + Pr (Г ₀) Pr (A ú Г ₀) =

= p ₁ p ₂ (1 - q ₁₂) + p ₁ (1- p ₂) (1 - q ₁) +

+ p ₂ (1- p ₁) (1 - q ₂) + (1- p ₁) (1- p ₂) (1 – q ₀).

Полная формула Байеса.

Как изменятся априорные вероятности гипотез Pr (Г_k) после опыта, в результате которого наблюдается событие A?

Заменяя в формуле Байеса (2.2.1) B на Г_k и используя (2.2.3), получим апостериорную вероятность (вероятность после опыта)

Pr (Г_k ÷ A) = Pr (Г_k) Pr (A ÷ Г_k) / 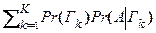. (2.2.4)

Пример2.2.3: на рынок поставляются приборы (стиральные машины). Известно, что 40% из них собираются из высококачественных деталей. Для приборов, собранных из высококачественных деталей, вероятность безотказной работы за время гарантии – 95%. Для приборов, собранных из обычных деталей, вероятность безотказной работы за время гарантии – 70%. Фирма закупила прибор и испытала его в течении времени гарантии. Прибор работал безотказно.

Какова вероятность того, что прибор собран из высококачественных деталей?

Решение: введем гипотезы

Г ₁ ‑ прибор собран из высококачественных деталей;

Г ₂ ‑ прибор собран из обычных деталей.

Априорные вероятность гипотез до опыта:

Pr (Г ₁) = 0,4; Pr (Г ₂) = 0,6.

Пусть A – событие безотказной работы в течение времени гарантии. Тогда

Pr (A ú Г ₁) = 0,95; Pr (A ú Г ₂) = 0,7. Следовательно, на основании (2.2.3) получим

Pr (Г ₁ ÷ A) = =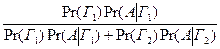

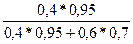= = 0,475.

Отсюда видно, что испытание повысило вероятность априорной гипотезы.

Пример2.2.4: два брокера на бирже независимо друг от друга делают ставки. Вероятность выигрыша для 1-го – 80%, для 2-го – 40%. Обнаружен выигрыш одного из них. Каковы апостериорные вероятности выигрышей брокеров?

Решение: примем за A событие выигрыша одним из брокеров и введем априорные вероятности

Г ₀ ‑ оба брокера проиграли; Pr (Г ₀) = 0,2 * 0,6 = 0,12;

Г ₁₂ ‑ оба выиграли; Pr (Г ₁₂) = 0,8 * 0,4= 0,32;

Г ₁ ‑ выиграл 1-ый; Pr (Г ₁) = 0,8 * 0,6= 0,48;

Г ₂ ‑ выиграл 2-ой; Pr (Г ₂) = 0,4 * 0,2= 0,08;

Pr (A ú Г ₀) = 0; Pr (A ú Г ₁₂) = 0; Pr (A ú Г ₁) = 1; Pr (A ú Г ₂) = 1.

Pr (Г ₁ ÷ A) = 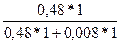= 6/7 = 86%,

Pr (Г ₂ ÷ A) = 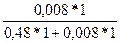= 1/7 = 14%.

Таким образом, факт выигрыша повышает шанс выигрыша брокера, обладающего большей квалификацией.

Пример2.2.5: фирма-производитель утверждает, что надежность ее оборудования – 98%. Заказчик назначает аудитора (эксперта) и тот утверждает, что надежность ‑ 90%. Заказчик сам считает, что заявление изготовителя верно на 40%, а эксперта ‑ на 60%. Далее заказчик проводит испытание двух единиц оборудования. Если оба испытания неудачны, то каково будет мнение заказчика о производителе и эксперте?

Решение: примем за A событие двух неудач;

Г ₁ ‑ прав производитель; Pr (Г ₁) = 0,4;

Г ₂ ‑ прав эксперт; Pr (Г ₂) = 0,6;

Pr (A ú Г ₁) = 0,02 *0,02 = 0,0004; Pr (A ú Г ₂) = 0,1 *0,1= 0,01.

Тогда

Pr (A) = Pr (Г ₁) Pr (A ú Г ₁) + Pr (Г ₂) Pr (A ú Г ₂) =

= 0,4*0,0004 + 0,6*0,01 = 0,00616;

Pr (Г ₁ ÷ A) = 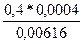= 0,03;

Pr (Г ₂÷ A) = 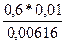= 0,97.

2.3. Вероятностное описание экономических объектов

при повторении опытов.

Пусть производятся сделки с различными фирмами. Результатом каждой сделки может быть некоторое событие A (успех). Нас интересует общее число успехов.

В общем случае говорят, что производят несколько опытов, приводящих к событию A в каждом из них. Необходимо уметь определять вероятность любого заданного числа появления события A в результате серии опытов.

Частная теорема и повторение опытов.

Задача решается наиболее просто, когда опыты являются независимыми.

Например, мы выбрали наугад несколько магазинов Москвы и хотим купить один и тот же товар. Если все данные магазины получают товар от различных поставщиков (с различных баз), то наши опыты независимы. Вероятность того или иного исхода каждого из опытов не зависит от того, какие исходы имели другие опыты.

В этом случае вероятность события A во всех опытах одинакова – Pr (A) = p.

Пример 2.3.1: проводятся переговоры о заключении сделки с тремя фирмами. Вероятность заключения сделки – p.

Найти вероятность того, что мы заключим хотя бы две сделки.

Решение: обозначим: B ₂₃ – событие заключения двух сделок в трех опытах; A ₁ – событие заключения сделки с 1-ой фирмой; A ₂ – событие заключения сделки со 2-ой фирмой; A ₃ – событие заключения сделки с 3-ей фирмой.

Событие B ₂₃ (заключения двух сделок в трех опытах) может произойти тремя независимыми способами (вариантами), как показано на рис. 2.3.1:

1) сделка A ₁, сделка A ₂, не заключение сделки ;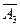

2) сделка A ₁, не заключение сделки 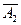; сделка A ₃;

3) не заключение сделки 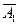, сделка A ₂, сделка A ₃.

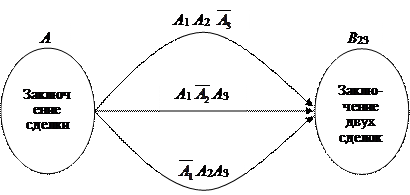Рис. 2.3.1

Следовательно:

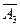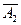B ₂₃ = A ₁ A ₂ + A ₁ A₃ + 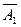A ₂ A ₃.

Так как все три варианта несовместимы, а события A ₁, A ₂ и A ₃ независимы, то

Pr (B ₂₃) = Pr (A ₁ A ₂ 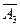) + Pr (A ₁ 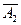A₃) + Pr ( 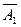A ₂ A ₃) =

= pp (1 – p) + p (1 – p) p + (1 – p) p p.

Обозначая 1 – p = q, получим

Pr (B₂₃) = 3 p ² q. (2.3.1)

Пример 2.3.2: производится «N» независимых опытов, в каждом из которых может появиться или не появиться некоторое событие A. Вероятность появления события A – Pr (A) = p, а вероятность не появления – q = 1 – p. Требуется найти вероятность Pr_MN (A) того, что событие A в этих «N» опытах появится ровно «M» раз.

Решение: используя технику примера 2.3.1, получим

B_MN = A ₁ A ₂ … A_M … +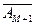

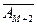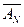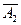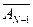+ A ₁ A ₃ … A_N +

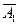
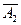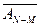
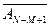+ … … A_N. (2.3.2)

В каждом слагаемом (2.3.2) событие A входит «M» раз, а 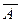– «N - M» раз. Тогда

(2.3.3)

где 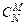= 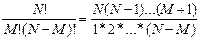– число сочетаний из N по M.

В связи с тем, что вероятность Pr (B_MN) в (2.3.3) по форме представляет собой члены разложения бинома

(q + p) ^N = 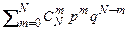, (2.3.4)

распределение вероятности Pr (B_MN) называют биномиальным распределением.

Общая теорема и повторение опытов.

Пусть вероятность появления события A в «i»-ом опыте – p_i, а вероятность не появления – q_i = (1- p_i), где i = 1, 2, …, N). Запись

B_MN = A ₁ A ₂ … A_M … +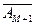

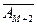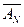+ A ₁ 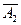A ₃ … 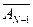A_N + …

описывает событие, состоящее в том, что событие A появилось «M» раз в «N» опытах. Тогда

Pr (B_MN) = p ₁ p ₂… p_M q_{M+ 1} … q_N + … +

+ p ₁ q ₂ p ₃ … q_{N- 1} p_N + …. (2.3.5)

Для расчета вероятности Pr (B_MN) вводят вспомогательную, так называемую, производящую функцию

j_N (z) = (q ₁ + p ₁ z) (q ₂ + p ₂ z) … (q_N + p_N z) =

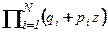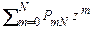= = . (2.3.6)

Оказывается, что все коэффициенты P_mN данной функции в точности равны вероятностям Pr (B_mN) появления события A ровно «m» раз в «N» опытах

Для частного случая, когда все p_i = p

j_N (z) = (q + p z) (q + p z) … (q + p z) =

= (q + p z) ^N = 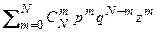. (2.3.7)

Отметим условие

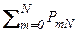= 1, (2.3.8)

которое следует из определения j_N (z) при z º 1 (так как q_i + p_i = = 1) и из того, что события B_0N, B_1N, B_2N, …, B_NN образуют полную группу несовместных событий (так как P_mN – вероятность появления события A «m» раз в «N» опытах).

Групповые события.

Обозначим C_MN событие, состоящее в том, что событие A появится не менее «M» раз в «N» опытах. Очевидно, что

C_MN = B_MN + B_{M+ 1 N} + … + B_NN,

Pr (C_MN) = Pr (B_MN) + Pr (B_{M+ 1 N}) + …+ Pr (B_NN) =

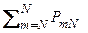= = 1 - 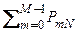. (2.3.9)

Пример2.3.3: проводится 4-ре независимых переговоров с 4-мя фирмами о заключении одного и того же соглашения (A). Вероятности заключения соглашения: p ₁ = 0,1; p ₂ = 0,2; p ₃ = 0,3; p ₄ = 0,4.

Найти вероятности: P ₀₄ – вероятность ни одного соглашения; P ₁₄ – вероятность одного соглашения; P ₂₄ – вероятность двух соглашений; P ₃₄– вероятность трех соглашений; P ₄₄ – вероятность четырех соглашений.

Решение: воспользуемся производящей функцией из (2.3.7)

j ₄(z) = (q ₁ + p ₁ z) (q ₂ + p ₂ z) (q ₃ + p ₃ z) (q ₄ + p ₄ z) =

= (0,9 + 0,1 z) (0,8 + 0,2 z) (0,7 + 0,3 z) (0,6 + 0,4 z) =

= 0,302 + 0,440 z + 0,215 z ² + 0,040 z ³ + 0,002 z ⁴.

Таким образом P ₀₄ = 0,302; P ₁₄ = 0,440; P ₂₄ = 0,215; P ₃₄ = 0,040; P ₄₄ = 0,002.

Пример2.3.4: при поиске делового партнера среди всех возможных менеджер 4-ре раза обратился к одной и той же фирме по телефону. Вероятность телефонной связи с этой фирмой при каждом обращении равна p = 0,3 (3 связи при 10-ти звонках). Известно также, что для успешного заключения контракта достаточно двух переговоров с фирмой. При однократном переговоре вероятность заключения контракта равна 0,6. Найти вероятность события A – заключения контракта с фирмой.

Решение: выдвинем две гипотезы: Г ₀ – связь с фирмой не состоялась; Г ₁– связь с фирмой состоялась 1 раз. Рассчитаем вероятность Pr (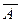) не заключения контракта с фирмой

Pr (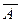) = Pr (Г ₀) Pr ( 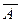÷ Г ₀) + Pr (Г ₁) Pr ( 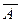÷ Г ₁).

Pr (Г ₀) = P ₀₄ = (1- p)⁴ = (0,7)⁴ = 0,240;

Pr (Г ₁) = P ₁₄ = 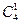p q ³ = 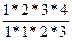* 0,3*(0,7)³ = 0,412;

Pr (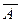 ÷ Г ₀) = 1, Pr ( 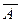÷ Г ₁) = 1 – 0,6 = 0,4;

Следовательно: Pr (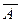) = 0,240 + 0,412 * 0,4 = 0,405, а Pr (A) = 1 – Pr (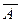) = 0,595.

2.4. Функции распределений вероятностей

непрерывных случайных величин.

Случайные величины и законы их распределений.

Рассмотренные в разделах 2.1 ¸ 2.3 вероятностные описания ЭО были в основном связаны с дискретными случайными величинами, характеризовавшими как их динамические переменные, так и параметры структурного описания. Любая величина называется дискретной случайной величиной, если множество ее возможных значений конечно или счетно и принятие ею каждого из указанных значений есть случайное событие с определенной вероятностью.

Для вероятностного описания состояний ЭО зачастую используют непрерывные случайные величины, характеризующие их динамические переменные, и функции их распределения.

Функцией F (s) распределения вероятностей случайной величины S называется вероятность того, что она примет значение, не превосходящее число s

F (s) = Pr (S £ s). (2.4.1)

Если функция распределения F (s) непрерывна и дифференцируема, то ее производная ¶ F (s)/ ¶ s называется плотностью распределения вероятностей p (s). Тогда функцию распределения вероятности можно определить как

F (s) = Pr (S £ s) = 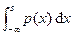. (2.4.2)

Из определения функции F (s), что она не убывает с ростом своего аргумента s.

В принципе, по аналогии с (2.4.2) можно ввести функцию распределения вероятностей и для дискретной случайной величины

F (s) = Pr (S £ s) = 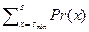. (2.4.3)

Заметим, что у дискретной случайной величины функция распределения ступенчатая, т.к. отражает сумму накопленных вероятностей Pr (x) случайных величин. Значение функции F (s) изменяется скачком при переходе с одного дискретного значения s на другое, как показано на рис. 2.4.1.

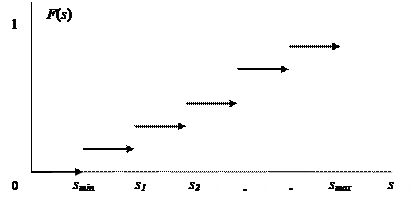Рис. 2.4.1

Нормальная плотность распределения вероятностей.

В силу того обстоятельства, что любая помеха H, сопутствующая какой либо динамической переменной или параметру структурного описания ЭО, зависит от огромного числа возмущающих факторов, возможно выдвинуть гипотезу о ее нормальном распределении, опираясь на центральную предельную теорему.

Как известно, центральная предельная теорема гласит, что распределение суммарного (аддитивного) значения бесконечно большого числа независимых случайных величин описывается нормальным законом Гаусса (независимо от законов распределений этих величин). В условиях выдвинутой гипотезы, плотность распределения вероятностей p (H) или отклонений H = S – á S ñ «N»-компонентного вектора состояния S от центрального (наиболее вероятного) вектора состояния á S ñ ЭО определяется многомерным нормальным законом распределения

p_нор (H) = p_нор (S) =

= exp [– (S – á S ñ) ⁺ COV ^-1 (S – á S ñ)]/(2 p) ^{N/ 2}ú COV ú^1/2, (2.4.4)

где (S – á S ñ) ⁺ ‑ транспонированный вектор (S – á S ñ), COV –ковариационнаяматрица размера N * N

COV = á(S – á S ñ)(S – á S ñ)⁺ ñ. (2.4.5)

Закон (2.4.4) можно рассматривать как закон распределения плотности вероятности помех H, так и самих случайных векторов состояний S.

В (2.4.4) и (2.4.5) áñ – операция математического ожидания, т.е. теоретического усреднения или усреднения по генеральной совокупности (см. подразделы «Статистики наблюдений …» и «Несмещенность …»); COV ^{- 1} – матица, обратная COV, ú COV ú ‑ детерминант матрицы COV. Выражаясь конкретнее, если S_n есть “ n ”-ый компонент S, á S_k ñ есть «k»-ый компонент á S ñ, а cov_nk есть «nk»-ый компонент COV, то

сov_nk = s_nk = á(S_n – á S_n ñ)(S_k – á S_k ñ)ñ. (2.4.6)

Диагональный элемент

сov_nn = D (S_n) = var (S_n) = s_n ² = á(S_n – á S_n ñ)²ñ (2.4.7)

есть дисперсия (вариация) S_n, где s_n называется среднеквадратичным или стандартным отклонением S_n от á S_n ñ. Если S_n и S_k статистически независимы, то cov_nk = 0 для " n ¹ k. В этом случае

p_нор (S) = exp [–(S ₁ – á S ₁ñ)²/2 s ₁²]/(2 p)^1/2 s ₁ ´ …

× exp [–(S_N – á S_N ñ)²/2 s _N ²]/(2 p)^1/2 s _N, (2.4.8)

т.е. многомерный нормальный закон распределения описывается произведением N одномерных нормальных законов

p_нор (S_n) = exp [– (S_n – á S_n ñ)²/2 s _n ²]/(2 p)^1/2 s _n . (2.4.9)

Нормальные законы распределений (одномерные и многомерные) широко используются при описании стохастических состояний ЭО даже в тех случаях, когда не выполняются условия центральной предельной теоремы. Тогда распределение (2.4.4) является некоторой моделью некоего истинного распределения Pr_ист (S).

Привлекательность распределений типа (2.4.4) связана с тем, что они являются параметрическими, т.е. зависят от конечного числа параметров á S ñ, COV.

Наглядное представление нормальной двумерной плотности распределения для двумерного вектора состояний S =(S ₁, S ₂) приведено на рис. 2.4.2 в виде функции двух переменных (рис. 2.4.2а) и в виде диаграммы разброса случайных выборок (рис. 2.4.2б).

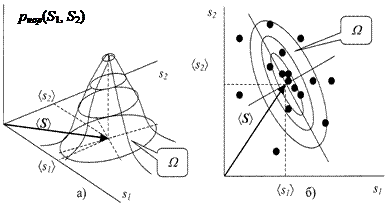
Рис. 2.4.2

Выборки нормально распределенной случайной величины имеют тенденцию попадать в одну область или кластер W.. Центр кластера определяется вектором á S ñ среднего значения, а форма – ковариационной матрицей COV. Из (4.4.4) и рис. 2.4.2б следует, что точки постоянной плотности образуют эллипсоид (в многомерном случае – гиперэллипсоид), для которого квадратичная форма (S – á S ñ) ⁺ COV ^{– 1}(S – á S ñ) постоянна. Главные оси этого гиперэллипсоида задаются собственными векторами ковариационной матрицы COV.