F(x) ® max

при ограничениях:

g_j(x)£b_j, j = 1,2,3,... m (5.6)

Здесь: F(x) — целевая функция, выражающая главную цель данной задачи — максимизировать прибыль. Таким образом, F(x) представляет собой математическое выражение, описывающее прибыль через управляющие переменные х. Переменные же х = (х₁, х₂,... x_n)— это искомые объемы выпуска соответствующего вида продукции;

b_j = (b₁, b₂,..., b_m) — величины соответствующих ресурсов предприятия;

g_j(x) = (g₁(x), g₂(x),..., g_m(x)) — текущие суммарные расходы ресурсов предприятия при фиксированных объемах выпуска каждого вида продукции. Эти расходы не должны превышать величин соответствующих ресурсов, которыми располагает предприятие.

При известных расчетных величинах прибыли на единицу объема выпуска каждого вида продукции целевая функция F(x), отражающая величину суммарной прибыли предприятия по всем видам продукции в зависимости от объемов выпуска х = (х₁, х₂,... x_n), может быть представлена в виде:

, (5.7)

где с₁, с₂, с₃,..., с_n — удельные (рассчитанные на единицу объема выпуска) величины прибыли по каждому виду продукции;

n — количество видов выпускаемой продукции (номенклатура).

Система ограничений по ресурсам может быть записана следующим образом:

— ограничение по 1 -му ресурсу:

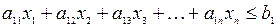
— ограничение по 2-му ресурсу:

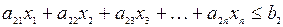
— ограничение по 3-му ресурсу:

……………………………………………………………………………………….

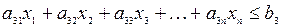
— ограничение по m -му ресурсу:

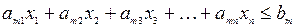(5.8)

(всего m ресурсов).

В системе ограничений (5.8) а₁₁, а₁₂, а₁₃,..., а₂₁, а₂₂, а₂₃... и т.д. — расходы соответствующих ресурсов на единицу объема выпуска каждого вида продукции. Система ограничений (5.8) должна быть дополнена требованиями неотрицательности всех х, так как объемы выпуска по смыслу задачи не могут выражаться отрицательными числами.

Таким образом, математическая модель оптимизацииобъемов выпуска продукции по критерию максимума прибыли записывается в виде:

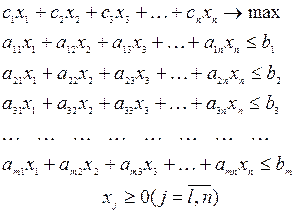(5.9)

Математическая модель (5.9) предполагает неограниченные потребности рынка на все виды продукции (не ограничены объемы выпуска сверху) и отсутствие обязательных поставок (не ограничены объемы выпуска снизу). Если же запросы рынка (возможность сбыта) по каким-либо (или по каждому) видам продукции ограничены, а также имеются ограничения снизу в виде обязательных объемов выпуска по заключенным договорам или в связи с внутренними потребностями (данная продукция как сырье или материалы используется в собственном производстве), то математическая модель должна быть дополнена соответствующей группой ограничений по минимальным и максимальным объемам поставок по каждому виду продукции. Такие ограничения имеют вид:

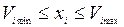(5.10)

Возможна и другая формулировка задачи управления: найти оптимальные объемы выпускаемой продукции х = (х₁, х₂,... x_n),обеспечивающие минимум издержек (затрат производства) при сохранении установленного суммарного уровня прибыли (или выручки) A_min.

В этом случае целевая функция математической модели управления имеет вид, по структуре аналогичный формуле (5.7), с той однако разницей, что в этом случае целевая функция представляет собой суммарные издержки производства при объемах выпуска продукции х = (х₁, х₂,... х_п).

, (5.11)

Здесь с₁, с₂, с₃,..., с_n — удельные (рассчитанные на единицу объема выпуска) величины затрат по каждому виду продукции.

Ограничение по установленному уровню прибыли может быть записано следующим образом:

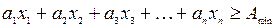(5.12)

В формуле (5.12) а₁, а₂, а₃,..., а_п — удельные (рассчитанные на единицу объема выпуска) величины прибыли по каждому виду продукции, а правая часть неравенства представляет собой суммарную прибыль за заданный промежуток времени при объемах выпуска продукции х = (х₁, х₂,... х_п)за этот промежуток времени.

Ограничения по минимальным и максимальным объемам поставок продукции, как и ранее, имеют вид (5.10)

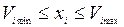
Таким образом, в такой постановке математическая модель верхнего иерархического уровня управления имеет вид:

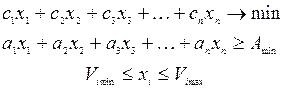(5.13)