 |
Главная Случайная страница Контакты | Мы поможем в написании вашей работы! | |
i , j ,k так, что бы вектор i совпал с ортом e оси . 3 страница
|
|
2.5. Барицентрические координаты. Деление отрезка в данном соотношении. Пучок прямых. Пучок плоскостей.
Положение точки  на отрезке
на отрезке  можно задать величиной
можно задать величиной 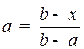 , показывающей в каком соотношении точка
, показывающей в каком соотношении точка  делит отрезок. Величина
делит отрезок. Величина 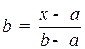 также определяет положение точки
также определяет положение точки  . Числа
. Числа 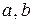 , однозначно определяющие положение точки на отрезке, называются барицентрическими координатами точки
, однозначно определяющие положение точки на отрезке, называются барицентрическими координатами точки  . Отметим следующие свойства барицентрических координат:
. Отметим следующие свойства барицентрических координат:
1.  .
.
2.  .
.
3. 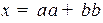 .
.
Середина отрезка имеет координаты: 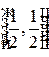 .
.
Рассмотрим три точки на плоскости или в пространстве: 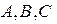 . Любая точка
. Любая точка  треугольника
треугольника  однозначно определятся тремя барицентрическими координатами:
однозначно определятся тремя барицентрическими координатами: 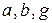 , обладающими следующими свойствами:
, обладающими следующими свойствами:
1.  .
.
2.  .
.
3. 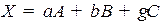 .
.
Линейные операции сложения и умножения на числа над точками определяются так же, как и над векторами. Например, третье условие можно записать в виде: 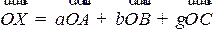 .
.
Геометрически числа 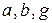 определяются отношениями площадей треугольников
определяются отношениями площадей треугольников  ,
, 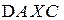 ,
,  ко всей прощади треугольника
ко всей прощади треугольника  (см. рис. 2.12).
(см. рис. 2.12).

Рис. 2.12. Барицентрические координаты
Если в вершины треугольника поместить одинаковые массы, то центр тяжести такой системы будет иметь барицентрические координаты 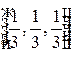 .
.
Так же как для треугольника вводятся барицентрические координаты для тетраэдра 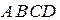 (не обязательно правильного). Положение внутренней точки
(не обязательно правильного). Положение внутренней точки  тетраэдра однозначно определяется четырьмя числами
тетраэдра однозначно определяется четырьмя числами  , удовлетворяющими следующим свойствам:
, удовлетворяющими следующим свойствам:
1.  .
.
2. 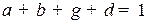 .
.
3. 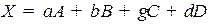 .
.
Геометрически барицентрические координаты равны отношениям объемов внутренних тетраэдров 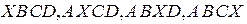 к объему тетраэдра
к объему тетраэдра 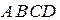 (см. рис. 2.13).
(см. рис. 2.13).

Рис. 2.13. Смысл барицентрических координат
Если в вершины тетраэдра поместить одинаковые массы, то центр тяжести такой системы будет иметь барицентрические координаты 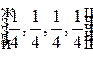 .
.
Свойство 2 барицентрических координат называют еще разбиением единицы.
С помощью барицентрических координат описывают положение прямых и плоскостей в пучках. Вначале дадим определение пучка прямых.
Рассмотрим точку, определяемую двумя не параллельными прямыми:
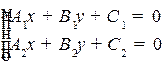 .
.
Множество всех прямых, проходящих через эту точку назывется пучком прямых. Между множеством всех прямых пучка и множеством разбиения единицы  имеется взаимно однозначное соответствие, именно, любая прямая из пучка
имеется взаимно однозначное соответствие, именно, любая прямая из пучка 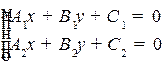 имеет свои барицентрические координаты
имеет свои барицентрические координаты 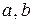 , с помощью которых записывается ее уравнение:
, с помощью которых записывается ее уравнение:
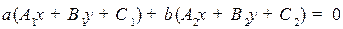 .
.
Аналогичное положение имеет место с пучком плоскостей.
Рассмотрим прямую, определяемую двумя плоскостями:  . Пучком плоскостей называется множество плоскостей, проходящих через эту прямую. Любая плоскость пучка имеет свои барицентрические координаты
. Пучком плоскостей называется множество плоскостей, проходящих через эту прямую. Любая плоскость пучка имеет свои барицентрические координаты 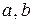 через которые записывается ее уравнение:
через которые записывается ее уравнение:
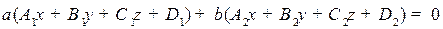 .
.
Пример. Даны уравнения сторон треугольника:  . Сотавить уравнение высоты, опущенной из вершины
. Сотавить уравнение высоты, опущенной из вершины 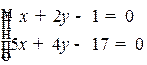 .
.
Эта высота принадлежит пучку 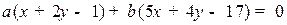 или, что тоже,
или, что тоже, 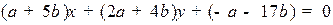 . Выпишем условие ортогональности высоты стороне
. Выпишем условие ортогональности высоты стороне 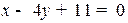 :
:
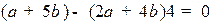 . Или
. Или 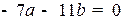 .
.
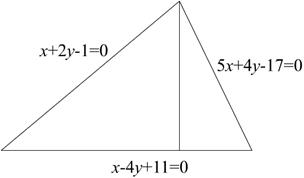
Рис. 2.14. Уравнения сторон треугольника
В уравнении прямой коэффициенты определяются с точностью до множетиля, отличного от нуля, поэтому возьмем 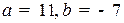 . Таким образом, уравнение высоты будет (см. рис. 2.14):
. Таким образом, уравнение высоты будет (см. рис. 2.14):
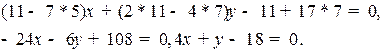
Геометрия – это исскуство правильно рассуждать над ни куда не годными рисунками. Давид Гильберт.

2.6. Расстояние от точки до прямой в пространстве
Дано: уравнение прямой в параметрическом виде: r = r0 + 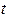 l и точка
l и точка  r1=
r1= 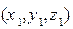 .
.
Первый способ.
1) Составлям уравнение плоскости, проходящей через точку 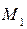 , перпендикулярно прямой:
, перпендикулярно прямой:
(r – r1, l)=0.
2) Находим точку пересечения прямой и построенной плоскости:
(r0 + 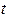 l – r1, l)=0,
l – r1, l)=0, 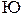
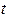 (l, l)= (r1 – r0 , l)
(l, l)= (r1 – r0 , l) 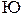
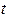 = (r1 – r0 , l) / (l, l). Радиус вектор искомой точки
= (r1 – r0 , l) / (l, l). Радиус вектор искомой точки 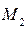 будет равен: r2 = r0 + l (r1 – r0 , l) / (l, l).
будет равен: r2 = r0 + l (r1 – r0 , l) / (l, l).
Находим расстояние между двумя точками 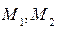 (см. рис. 2.15).
(см. рис. 2.15).

Рис. 2.15. Пересечение прямой и плоскости
Второй способ.
Строим параллелограмм на векторах 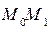 и l. Находим его площадь, как модуль векторного произведения и делим на длину основания
и l. Находим его площадь, как модуль векторного произведения и делим на длину основания  l
l  (см. рис. 2.16).
(см. рис. 2.16).

Рис. 2.16. Перпендикуляр на прямую
2.7. Определение координат точки пересечения прямой и плоскости в пространстве
Если прямая задана параметрически r = r0 + 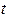 l и уравнение плоскости имеет вид: (r – r1, l)=0, то эта задача решалась в предыдущем параграфе.
l и уравнение плоскости имеет вид: (r – r1, l)=0, то эта задача решалась в предыдущем параграфе.
Если прямая задана в виде:  , то ее пересечение с плоскостью
, то ее пересечение с плоскостью  сводится к решению системы трех уравнений с тремя неизвестными (см. рис. 2.17)
сводится к решению системы трех уравнений с тремя неизвестными (см. рис. 2.17)

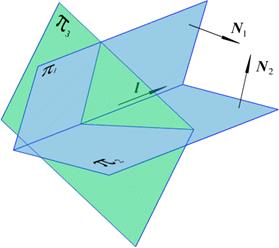
Рис. 2.17. Точка пересечения трех плоскостей
2.8. Определение координат проекции точки на прямую на плоскости, проекции точки на плоскость в пространстве
Проекция точки 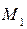 на прямую (r – r0, N)=0 на плоскости.
на прямую (r – r0, N)=0 на плоскости.
Если прямая задана общим уравнением 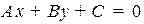 , N =
, N = 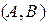 , то составляется уравнение прямой r = r1 +
, то составляется уравнение прямой r = r1 + 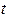 N, проходящей через точку
N, проходящей через точку 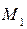 и направляющим вектором l = N. После чего находится точка пересечения этой прямой с исходной прямой: (r1 +
и направляющим вектором l = N. После чего находится точка пересечения этой прямой с исходной прямой: (r1 + 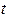 N – r0, N)=0
N – r0, N)=0 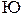
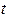 (N, N)= (r0 – r1, N). Радиус вектор этой точки будет равен: r = r1 + N (r0 – r1, N) / (N, N) (см. рис. 2.18).
(N, N)= (r0 – r1, N). Радиус вектор этой точки будет равен: r = r1 + N (r0 – r1, N) / (N, N) (см. рис. 2.18).
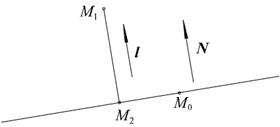
Рис. 2.18. Проекция точки на прямую
Аналогично решается задача нахождения проекции точки 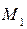 на плоскость
на плоскость
(r – r0, N)=0 в пространстве. В векторном виде решение выглядит точно так же, как и в плоском случае.
Уравнение проектирующей прямой: r = r1 + 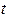 N, радиус вектор-проекции будет равен:
N, радиус вектор-проекции будет равен: 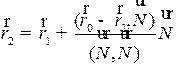 (см. рис. 2.19)
(см. рис. 2.19)
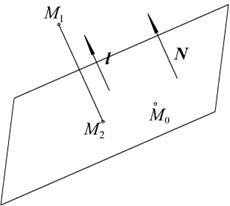
Рис. 2.19. Проекция точки на плоскость
2.9. Базовые задачи
Напоминание.
Прямую, проходящую через точку 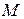 с направляющим вектором
с направляющим вектором 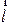 мы договорились обозначать
мы договорились обозначать 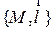 .
.
2.9.1. Составить уравнение плоскости, проходящей через три точки
Три точки 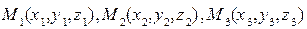 . Точки искомой плоскости
. Точки искомой плоскости  удовлетворяют условию: вектора
удовлетворяют условию: вектора 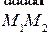 ,
, 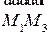 ,
, 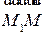 должны быть компланарны, то есть, должно быть равно нулю смешанное произведение (см. рис. 2.20)
должны быть компланарны, то есть, должно быть равно нулю смешанное произведение (см. рис. 2.20)
(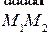 ,
, 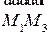 ,
, 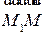 )=0,
)=0,
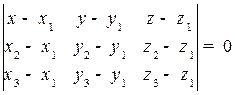 .
.
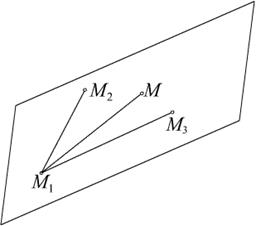
Рис. 2.20. Уравнение плоскости по трем точкам
2.9.2. Составить уравнение плоскости, проходящей через точку и прямую
Дана точка 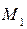 и прямая r = r0 +
и прямая r = r0 + 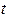 l.
l.
Точки искомой плоскости  удовлетворяют условию: вектора
удовлетворяют условию: вектора  , l,
, l,  должны быть компланарны. Искомое уравнении плоскости:
должны быть компланарны. Искомое уравнении плоскости:
( , l,
, l,  ) = 0.
) = 0.
2.9.3. Составить уравнение плоскости, проходящей через заданную точку, параллельно заданной плоскости
Дана точка  и плоскость
и плоскость 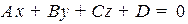 .
.
У искомой плоскости общий перпендикуляр с заданной плоскостью, поэтому уравнение искомой плоскости будет: 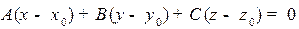 .
.
2.9.4.Составить уравнение плоскости, проходящей через заданную прямую, параллельно заданному вектору
Дана прямая с точкой 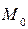 и направляющим вектором
и направляющим вектором 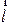 . Искомая плоскость будет иметь нормаль
. Искомая плоскость будет иметь нормаль  (см. рис. 2.21).
(см. рис. 2.21).
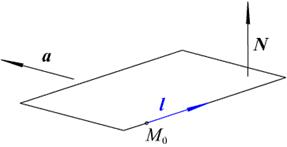
Рис. 2.21. Уравнение плоскости через точку
2.10. Разные задачи
2.10.1. Определить расстояние между двумя скрещивающимися прямыми
Первый способ. Заданы прямые:
r = r1 + 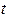 l1, r = r2 +
l1, r = r2 + 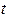 l2.
l2.
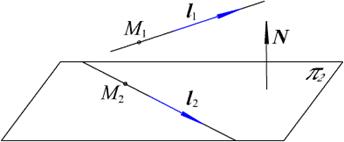
Рис. 2.22. Расстояние между прямыми
1) Вектор, перпендикулярный обеим прямым N = [l1, l2].
2) По N и точке 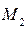 составляем уравнение плоскости
составляем уравнение плоскости 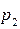 , проходящей через вторую прямую, параллельно первой прямой: плоскость, проходящую через точку
, проходящей через вторую прямую, параллельно первой прямой: плоскость, проходящую через точку 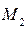 с нормалью N.
с нормалью N.
3) Находим расстояние от точки 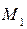 до плоскости
до плоскости 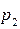 (см. рис. 2.22).
(см. рис. 2.22).
Второй способ.
Находим высоту параллелепипеда, построенного на векторах l1, l2, 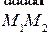 , в основании которого лежит параллелограмм, построенный на l1, l2 (см. рис. 2.23).
, в основании которого лежит параллелограмм, построенный на l1, l2 (см. рис. 2.23).
Ответ:  .
.
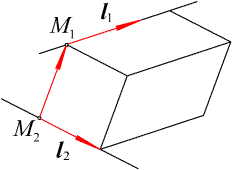
Рис. 2.23. Высота паллелепипеда
2.10.2. Определить расстояние между двумя параллельными прямыми

Рис. 2.24. Расстояние между параллельными прямыми
Задача решается одинаково, как для плоского, так и для пространственного случаев (см. рис. 2.24). Искомое расстояние равно высоте параллелелограмма, построенного на векторах l1, 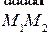 с основанием l1.
с основанием l1.  .
.
2.10.3. Составить уравнение прямой, проходящую через точку 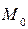 , заданную прямую, определяемую точкой
, заданную прямую, определяемую точкой 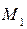 , направляющим вектором
, направляющим вектором 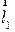 и параллельно плоскости
и параллельно плоскости 
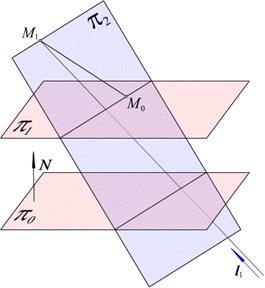
Рис. 2.25. Уравнение прямой
Уравнение прямой будем искать в виде пересечения двух плоскостей (см. рис. 2.25).
1) Первая плоскость  определяется точкой
определяется точкой 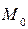 и нормалью
и нормалью 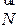 .
.
2) Вторая плоскость 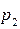 проводится через точку
проводится через точку 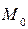 и прямую
и прямую 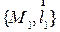 . Таким образом, эта плоскость проходит через
. Таким образом, эта плоскость проходит через 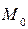 и имеет нормаль
и имеет нормаль 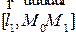 .
.
2.10.4. Составить уравнение общего перпендикуляра двух скрещивающихся прямых
Общий перпендикуляр будем искать в виде пересечения двух плоскостей  ,
, 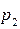 .
.

Рис. 2.26. Общий перпендикуляр
Последовательность действий (см. рис. 2.26):
1) общий перпендикуляр к прямым будет 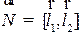
2) нормаль к плоскости  , проходящей через прямую
, проходящей через прямую 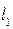 перпендикулярно
перпендикулярно 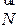 :
:

3) сама плоскость  определяется точкой
определяется точкой 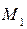 и указанной нормалью
и указанной нормалью
 .
.
4) нормаль к плоскости 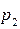 проходящей через прямую
проходящей через прямую 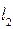 перпендикулярно
перпендикулярно 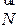 :
:

5) сама плоскость 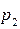 определяется точкой
определяется точкой 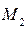 и указанной нормалью
и указанной нормалью
 .
.
2.10.5. Составить уравнение плоскости, проходящей через прямую с точкой 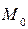 , направляющим вектором
, направляющим вектором 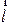 , перпендикулярно плоскости
, перпендикулярно плоскости  , проходящей через точку
, проходящей через точку 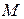 с нормалью
с нормалью 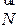 .
.
Точка 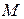 для решения задачи не понадобится и на рисунке она не показана.
для решения задачи не понадобится и на рисунке она не показана.
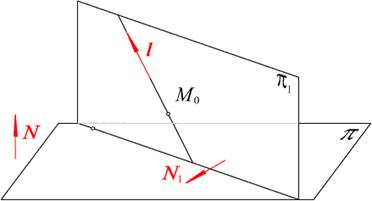
Рис. 2.27. Уравнение плоскости
1) Находим перпендикуляр 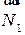 к искомой плоскости (см. рис. 2.27):
к искомой плоскости (см. рис. 2.27):
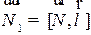 .
.
2) Искомая плоскость  будет определяться точкой
будет определяться точкой 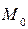 и нормалью
и нормалью 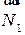 .
.
2.10.6. Проекция точки на прямую в пространстве
Задана прямая 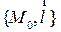 и точка
и точка 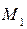 .
.
1) Строим проектирующую плоскость  , проходящую через точку
, проходящую через точку 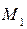 с нормалью
с нормалью 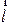 .
.
2) Находим точку пересечения плоскости  и прямой
и прямой 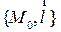 .
.
2.10.7. Симметричная точка относительно плоскости
Дана плоскость  , определяемая точкой
, определяемая точкой 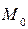 и нормалью
и нормалью 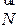 и точка
и точка  .
.
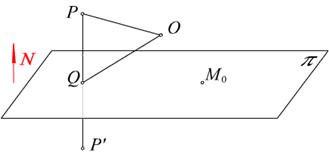
Рис. 2.28. Симметричная точка
1) Строится прямая  , проходящая через точку
, проходящая через точку  , перпендикулярно плоскоси
, перпендикулярно плоскоси  (см. рис. 2.28).
(см. рис. 2.28).
2) Находится точка  пересечения этой прямой с плоскостью.
пересечения этой прямой с плоскостью.
3) Искомая точка  находится из треугольника
находится из треугольника 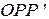 :
: 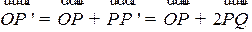 .
.
2.10.8. Симметричная точка относительно прямой в пространстве
Задана прямая 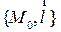 и точка
и точка  .
.
1) Находим проекцию  точки
точки  на прямую, как это описывалось в пункте 2.10.6.
на прямую, как это описывалось в пункте 2.10.6.
2) Искомая точка  находится из треугольника
находится из треугольника 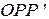 :
: 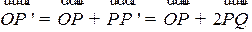 (см. рис. 2.29).
(см. рис. 2.29).
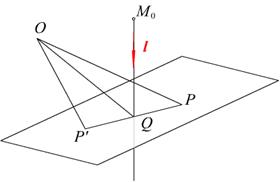
Рис. 2.29. Симметричная точка относительно прямой
2.10.9. Уравнение плоскости, проходящей через прямую, параллельно другой прямой
Заданы прямые 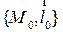 ,
, 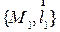 .
.
Плоскость  , проходящая через первую прямую, параллельно второй прямай определяется, как плоскость, проходящая через
, проходящая через первую прямую, параллельно второй прямай определяется, как плоскость, проходящая через 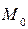 с нормалью
с нормалью 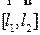 .
.
2.10.10. Уравнение прямой, параллельной плоскостям и пересекающей две прямые
Прямая задана пересечением плоскостей  . Две прямые имеют направляющие векторы l1, l2 (см. рис. 2.30).
. Две прямые имеют направляющие векторы l1, l2 (см. рис. 2.30).
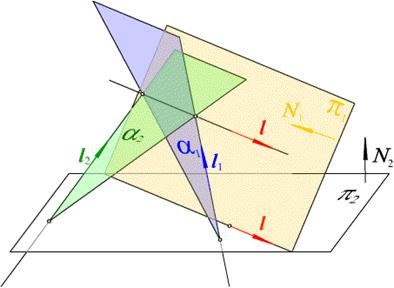
Рис. 2.30. Уравнение прямой
1) Находим направляющий вектор 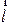 прямой
прямой  :
: 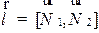 .
.
Дата публикования: 2014-11-18; Прочитано: 528 | Нарушение авторского права страницы | Мы поможем в написании вашей работы!
