i , j ,k так, что бы вектор i совпал с ортом e оси . 2 страница

1.7.1. Определение.

Смешанным произведением трех векторов a, b, c назвается выражение

([ a, b ], с). Обозначается смешанное произведение (a, b, c).

(a, b, c) = ([ a, b ], с).

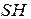Из определения получаем: (a, b, c) = [ a, b ] с = , где 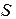- площадь основания, а 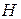- высота параллелепипеда, построенного на векторах

a, b, c. Модуль смешанного произведения (a, b, c) равен объему параллелепипеда, построенного на векторах a, b, c. (a, b, c) > 0, если тройка векторов – правая, (a, b, c) < 0, если тройка векторов – левая, (a, b, c) = 0, если тройка векторов компланарная (см. рис. 1.23).

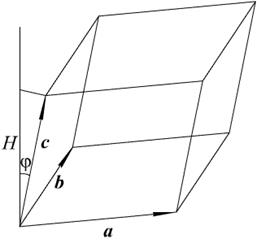
Рис. 1.23. Модуль смешанного произведения

Slide_1_23 «Геометрический смысл смешанного произведения»

Следствие. (a, b, c) = ([ a, b ], с) =(a,[ b, c ]).

Равенство нулю смешанного произведения означает компланарность векторов a, b, c.

1.7.2. Выражение смешанного произведения в декартовых координатах

Если x =x ₁ i + x ₂ j + x ₃ k, y =y ₁ i + y ₂ j + y ₃ k, z =z ₁ i + z₂ j + z ₃ k, то

(x, y, z) = .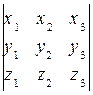

Доказательство:

(x, y, z) = ([ x, y ], z) = ((x ₂ y ₃ – x ₃ y ₂ , x ₃ y ₁ – x ₁ y ₃, x ₁ y ₂ – x ₂ y ₁), c) =

=(x ₂ y ₃ – x ₃ y ₂ ) z ₁ +(x ₃ y ₁ – x ₁ y ₃) z₂ + (x ₁ y ₂ – x ₂ y ₁) z₃= .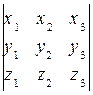

Slide_1_23_1 «Смешанное произведение»

Следствие. Необходимым и достаточным условием равенства нулю определителя

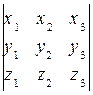= 0, является компланарность векторов

x = (x ₁, x ₂, x ₃), y = (y ₁, y ₂, y ₃), z = (z ₁, z₂, z ₃).

Глава 2. Прямые и плоскости

2.1. Уравнение прямой на плоскости и плоскости в пространстве, ортогональных данному вектору и проходящих через данную точку

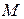Выпишем уравнение прямой, проходящей через точку , перпендикулярно заданному вектору N. Эта прямая может быть описана, как геометрическое место точек , для которых 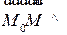N: 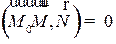. Последнее соотношение, записанное в декартовых координатах, будет выглядеть следующим образом:

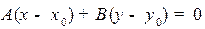, (1)

где N= 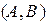-нормаль, 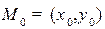, M= 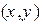- текущая точка на прямой (см. рис. 2.1).

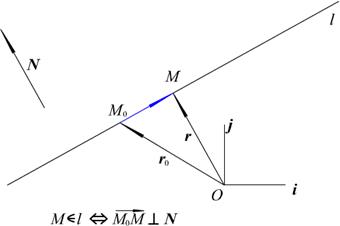
Рис. 2.1. Прямая на плоскости (общее уравнение)

Уравнение (1) называется общим уравнение прямой на плоскости. Уравнение (1) можно записать в векторном виде:

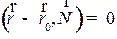(1)

Отметим, что условием того, что уравнение (1) представляет уравнение прямой должно выполняться условие .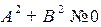

Аналогичные рассуждения можно провести и для плоскости в пространстве (см. рис. 2.2).

Рис. 2.2. Общее уравнение плоскости

Уравнение прямой, не проходящей через начало координат можно представить в виде (общее уравнение прямой 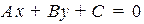поделить на )

.

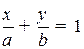Это уравнение называется уравнением прямой в отрезка. Геометрически числа 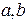имеют смысл отрезков, отсекаемых прямой на соответствующих осях.

Slide_2_2_1 «Уравнение прямой в отрезках»

Уравнение плоскости, проходящей через точку 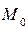, перпендикулярно заданному вектору N, представляет собой геометрическое место точек 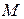, для которых 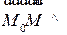N: 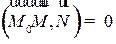. Последнее соотношение, записанное в декартовых координатах, будет выглядеть следующим образом:

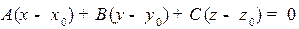, (2)

где N= 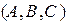-нормаль, 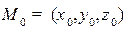, M= 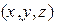. Или в векторном виде

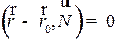(2)

Уравнения (2) называются общим уравнение плоскости в пространстве. Для краткости, в этом случае, будем говорить, что задана плоскость .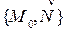

2.2. Общее уравнение первого порядка на плоскости и в пространстве, его исследование

2.2.1.Общее уравнение первого порядка на плоскости.

Рассмотрим общее уравнение первого порядка:

.

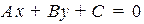Если 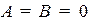, то при 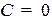это уравнение определяет всю плоскость (решением уравнения является любая точка 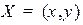на плоскости).

При 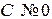уравнение не имеет решений и определяет, таким образом, пустое множество.

Если 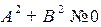, то уравнение имеет бесконечно много решений. Геометрически это множество является прямой на плоскости, перпендикулярной вектору 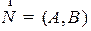. Действительно, пусть 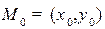некоторое решение уравнения 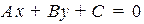: 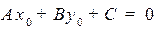. Тогда для любого решения 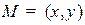этого уравнения будет справедливо равенство: 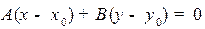, которое задает прямую на плоскости.

Slide_2_3_0 «Общее уравнении прямой на плоскости»

Отметим одно важное свойство общего уравнения прямой.

Отложим вектор нормали 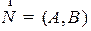из какой нибудь точки прямой, заданной уравнением 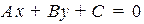. Пусть 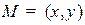какая либо точка плоскости, тогда

1) если 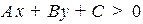, то точка 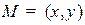лежит с той же стороны от прямой, что и вершина вектора ,

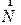2) если 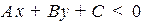, то точка 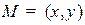и вершина 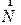лежат с разных сторон от прямой,

3) если 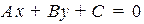,то точка 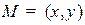принадлежит прямой (см. рис. 2.3.).

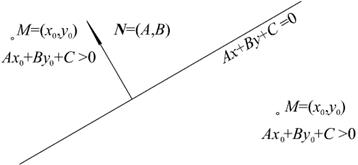
Рис. 2.3. Расположение точек относительно прямой

Докажем это утверждение. Пусть 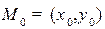точка прямой 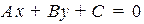, тогда 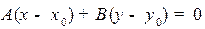и 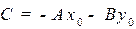. Если вектор 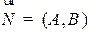отложен от прямой, например, из точки 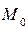, то условие того, что точка лежит в той же стороны от прямой, что и вершина вектора можно записать в виде . Обозначим этот случай а). Если с другой стороны, то 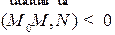. Обозначим этот случай b). Или в развернутом виде: 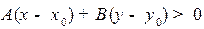в случае а) и 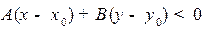в случае b). Итак, в первом случае 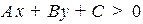, а во втором 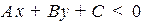(см. рис. 2.4).

Рис. 2.4. Разное расположение точек относительно прямой

2.2.2.Общее уравнение первого порядка в пространстве

Рассмотрим общее уравнение первого порядка в пространстве:

.

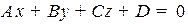Если 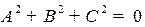, то это, либо все пространство (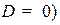, либо пустое множества ().

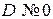Если 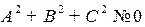, то это уравнение определяет плоскость с вектором нормали .

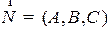Проверяется так же, как и для прямой на плоскости. Важное свойство общего уравнения плоскости в пространстве.

Отложим вектор нормали 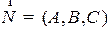из какой нибудь точки плоскости, заданной уравнением 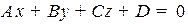. Пусть 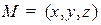какая либо точка пространства, тогда

1) если 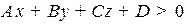, то точка 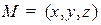лежит с той же стороны от прямой, что и вершина вектора ,

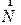2) если 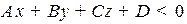, то точка 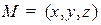и вершина 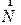лежат с разных сторон от прямой,

3) если 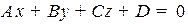,то точка принадлежит плоскости (см. рис. 2.5).

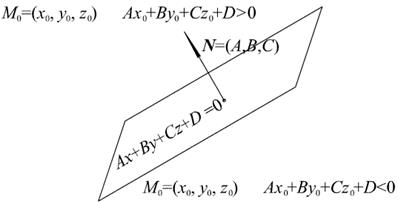
Рис. 2.5. Расположение точек относительно плоскости

Проверяется так же, как и для прямой на плоскости.

2.3. Нормальное уравнение прямой на плоскости и плоскости в пространстве. Приведение общего уравнения первого порядка к нормальному виду

2.3.1.Нормальное уравнение прямой на плоскости.

Рассмотрим общее уравнение прямой на плоскости.

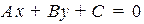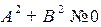, (1)

Определение. В случае 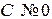нормальным уравнением прямой (1) называется уравнение

.

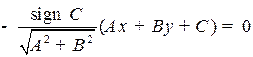Это уравнение можно записать в виде: 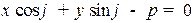(см. рис. 2.6)

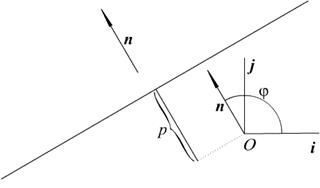
Рис. 2.6. Нормальное (нормированное) уравнение прямой

Slide_2_6 «Нормальное уравнение прямой»

n = 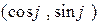– единичный вектор нормали, ориентированный так, что будучи отложенным из начала координат, он будут «смотреть» в сторону прямой.

Slide_2_6_1 «Нормировка уравнения прямой»

Пример. Пронормировать уравнение прямой .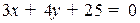

Модуль вектора нормали (3,4) равен 5. Делим уравнение прямой на 5 и берем знак противоположный знаку свободного коеффициента 25, получим нормальное уравнение прямой: .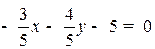

С помощью нормального уравнения прямой определяют расстояние от точек до прямых, именно:

Расстояние от точки до прямой 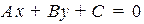с нормальным уравнением 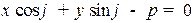равно

.

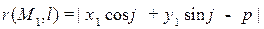Slide_2_6_2 «Расстояние от точки до прямой»

Пример. Найти расстояние от точки 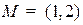до прямой 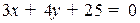(l).

.

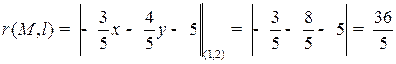2.3.2. Нормальное уравнение плоскости в пространстве

Рассмотрим общее уравнение плоскости в пространстве

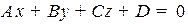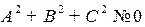, (1)

Определение. В случае 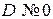нормальным уравнением плоскости (1) называется уравнение

.

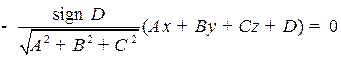Это уравнение можно записать в виде: 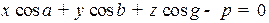(см. рис. 2.7)

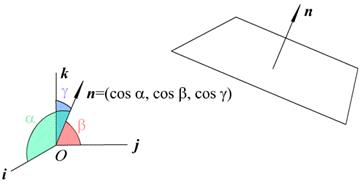
Рис. 2.7. Нормальное уравнение плоскости (через направляющие косинусы нормали)

n = 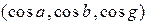– единичный вектор нормали, ориентированный так, что будучи отложенным из начала координат, он будут «смотреть» в сторону плоскости.

Пример. Пронормировать уравнение прямой .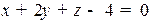

Модуль вектора нормали (1,2,1) равен 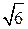. Делим уравнение прямой на 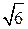и берем знак противоположный знаку свободного коеффициента -4, получим нормальное уравнение прямой: .

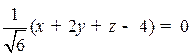С помощью нормального уравнения плоскости определяют расстояние от точек до плоскостей, именно:

Расстояние от точки 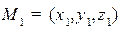до плоскости 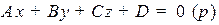с нормальным уравнением 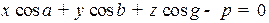равно

.

Пример. Найти расстояние от точки 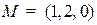до плоскости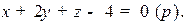

.

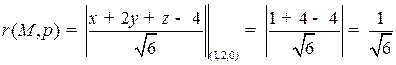2.4. Различные формы уравнения прямой на плоскости и в пространстве. Переход от одной формы к другой

2.4.1.Общее уравнение прямой на плоскости

Ранее уже рассматривалось уравнение прямой: 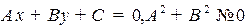, В векторной виде: .

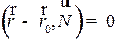2.4.2.Параметрическое уравнение прямой на плоскости

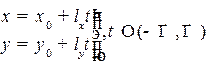, В векторном виде: r = r₀ + l , .

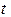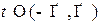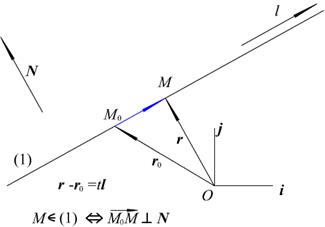
Рис. 2.8. Параметрическое уравнение прямой

Slide_2_8 «Параметрическое уравнение прямой на плоскости»

Вектор l называется направляющим вектором прямой (см. рис. 2.8).

2.4.3.Каноническое уравнение прямой на плоскости

Каноническое уравнение, в действительности, является несколько другой записью параметрического уравнения:

.

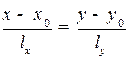Для канонического уравнения прямой, так же как и для параметрического уравнения, нужна точка на прямой и направляющий вектор. Для краткости, в этом случае, будем говорить, что задана прямая .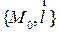

Slide_10_1 «Каноническое уравнение прямой на плоскости»

2.4.4. Переход от одной формы уравнения прямой к другой на плоскости

Не тривиальным является только переход от общего к уравнения к параметрическому и обратно.

От общего к параметрическому.

Общее уравнение определяется нормалью N и точко 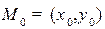на прямой. Если точка не задана, то ее можно найти, задав 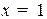(в случае 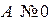) или 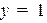(в случае 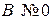) и решив уравнение 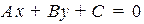относительно оставшейся неизвестной. Например, для уравнения 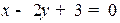полагаем 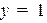и находим 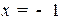, 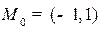. После того, как точка 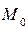найдена находим направляющий вектор прямой l. В качестве направляющего вектора берется любой вектор, ортогональный вектору нормали N. Для уравнения 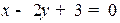таким вектором может служить вектор l= 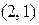. В параметрическом виде уравнение будет выглядеть следующим образом:

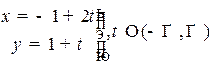, в каноническом: .

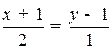От параметрического к общему.

Для обратного перехода дроби 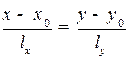формально преобразуются у виду: 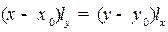и далее получаем общее уравнение прямой: .

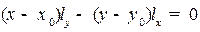Пример. Привести к общему виду уравнение 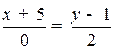. После указанных преобразований получим: .

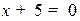2.4.5.Уравнение прямой в пространстве, как пересечение двух плоскостей

Прямую в пространстве можно задать, указав две плоскости, линией пересечения которых, является данная прямая. При этом используют следующую запись:

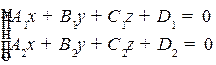
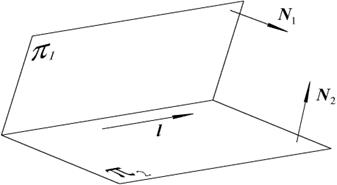
Рис. 2.9. Прямая, как пересечение двух плоскостей

Для того, чтобы указанные плоскости определяли прямую, они должны быть не параллельны, то есть вектора 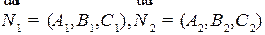не должны быть коллениарны (см. рис. 2.9).

2.4.6.Параметрическое уравнение прямой в пространстве

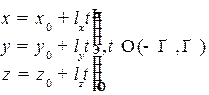, в векторном виде: r = r₀ + l 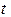, , 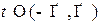(см. рис. 2.10).

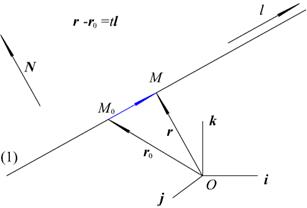
Рис. 2.10. Парметрическое уравнение прямой

2.4.7.Каноническое уравнение прямой в пространстве

Каноническое уравнение, в действительности, является несколько другой записью параметрического уравнения:

.

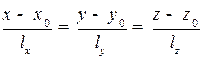Для канонического уравнения прямой, так же как и для параметрического уравнения, нужна точка на прямой и направляющий вектор. Для краткости, в этом случае, будем говорить, что задана прямая .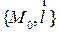

Slide_10_2 «Каноническое уравнение прямой в пространстве»

2.4.8. Переход от одной формы уравнения прямой к другой в пространстве

От общего к параметрическому

Задав какое нибудь значение одной из переменных 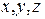, и решая систему

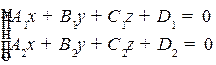относительно оставшихся переменных можно будет найти какую нибудь точку 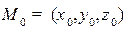на прямой. Направляющий вектор можно найти, как векторное произведение нормалей плоскостей, определяющих данную прямую: l = [ N₁, N₂ ].

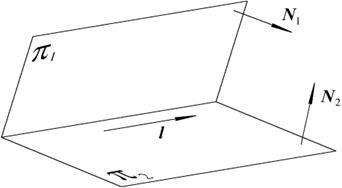
Рис. 2.11. Переход от одного уравнения к другому

От параметрического к общему

Из дробей 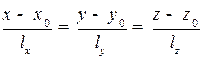формально выписываем два равенства: 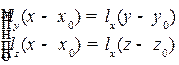, которые и дадут две плоскости, определяющие данную прямую (см. рис. 2.11).

2.4.9. Угол между двумя прямыми на плоскости и в простанстве, между двумя плолоскостями в пространстве, между прямой и плоскостью

Угол между двумя прямыми на плоскости равен углу между их нормалями. Угол между двумя прямыми в пространстве равен углу между их направляющими векторами. Угол между двумя плоскостями определяется, как угол между их нормалями. Угол между прямой и плоскостью в пространстве определяется, как угол между направляющим вектором прямой и нормалью к плоскости.