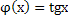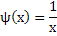|
Главная Случайная страница Контакты | Мы поможем в написании вашей работы! | |
Федеральное государственное бюджетное образовательное учреждение высшего профессионального образования 5 страница
|
|
7.3 ГРАФИЧЕСКОЕ РЕШЕНИЕ УРАВНЕНИЙ.
В отдельных случаях приближенное решение уравнения можно найти графическим методом. Пусть требуется найти корни уравнения 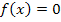 . Заменим это уравнение равносильным:
. Заменим это уравнение равносильным:
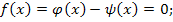
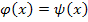 ;
;
где 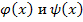 - более простые функции. Построим графики этих функций, получим корни уравнения
- более простые функции. Построим графики этих функций, получим корни уравнения  , как координаты x точек пересечения
, как координаты x точек пересечения 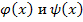 ;
;
ПРИМЕР: Решить уравнение 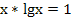 .
.
| Заменим его равносильным уравнением: 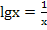 , где , где 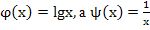 . Построив их графики, найдем точку пересечения . Построив их графики, найдем точку пересечения 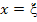 , которая и является решением исходного уравнения. , которая и является решением исходного уравнения.
|
7.4 МЕТОД ПОЛОВИННОГО ДЕЛЕНИЯ
(МЕТОД БИССЕКЦИИ).
Пусть требуется найти корень уравнения 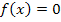 на отрезке [a,b]. Отрезок [a,b] либо задан заранее, либо получен методом отделения корней. Метод деления отрезка пополам проиллюстрирован на рисунке.
на отрезке [a,b]. Отрезок [a,b] либо задан заранее, либо получен методом отделения корней. Метод деления отрезка пополам проиллюстрирован на рисунке.
| Пусть  , в качестве начального приближения корня примем , в качестве начального приближения корня примем 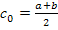 . Поскольку . Поскольку 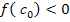 , то рассматриваем отрезок [ , то рассматриваем отрезок [ 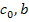 ]. Следующее приближение ]. Следующее приближение 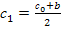 , при этом отрезок [ , при этом отрезок [ 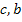 ] отбрасывается таким образом ] отбрасывается таким образом  . Аналогично находим другие приближения . Аналогично находим другие приближения 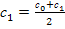 , и т.д. до выполнения условия , и т.д. до выполнения условия  . .
|
Итерационный процесс можно завершить тогда, когда значение функции 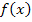 после к-ой итерации станет меньшим по модулю заданной
после к-ой итерации станет меньшим по модулю заданной 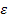 , т.е.
, т.е. 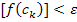 .
.
7.5 МЕТОД ХОРД
(ПРОПОРЦИОНАЛЬНЫХ ЧАСТЕЙ).
| Отрезок [a,b] либо задан заранее, либо получен методом отделения корней. Пусть 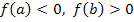 . Соединим хордой точки A и B, из подобия ∆ABC и ∆Ax1D: . Соединим хордой точки A и B, из подобия ∆ABC и ∆Ax1D:
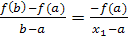 ,
x1 = a – ,
x1 = a –  . .
|
Это будет первым приближением к корню уравнения 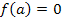 . Сравнивая знаки
. Сравнивая знаки 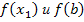 , видим, что корень находится на отрезке [x,b]. Следующее приближение к корню x2 получаем в точке пересечения с осью x ходы, соединяющей
, видим, что корень находится на отрезке [x,b]. Следующее приближение к корню x2 получаем в точке пересечения с осью x ходы, соединяющей 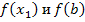 . Её координаты определяются аналогично, x1 по формуле:
. Её координаты определяются аналогично, x1 по формуле:
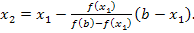
Последующие итерации выполняются по формуле:
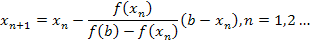
Итерации продолжаются до тех пор, пока значение 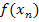 не станет меньше наперед заданного числа
не станет меньше наперед заданного числа 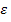 (погрешность расчета)
(погрешность расчета) 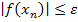 .
.
| Если 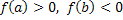 , то формула для расчета корня , то формула для расчета корня 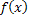 имеет вид имеет вид 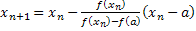 , погрешность приближенного решения можно оценить по формулам , погрешность приближенного решения можно оценить по формулам
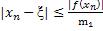 , где , где 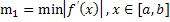 ; ;
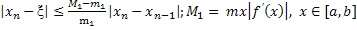 ,
где ,
где  - точное значение корня. - точное значение корня.
|
7.6 МЕТОД НЬЮТОНА
(МЕТОД КАСАТЕЛЬНЫХ).
Его отличие от предыдущего метода состоит в том, что вместо хорды проводится касательная кривой y=f(x) в точке c0. При этом не обязательно задавать отрезок [a,b], содержащий корень, а достаточно лишь найти начальное приближение корня. В точке c0 проводим касательную к кривой f(x). Точка пересечения её с осью дает первое приближение
| корня. Затем проводим перпендикуляр к оси x в точке x1 и получаем точку c1. Далее снова проводим касательную к f(x) в точке c1. Ее пересечение с осью x дает следующее приближение x2 и т.д., пока не будет выполнено условие 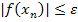 , где -погрешность расчета. , где -погрешность расчета.
|
Расчетную формулу можно получить из геометрических соображений из треугольника x1bc0 имеем:
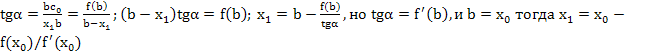 а для последующих точек
а для последующих точек 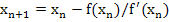 .
.
Оценка погрешности решения производится по формулам:
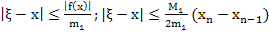 2
2
Здесь m1=min f’(x), а M1=max f’(x) на отрезке [a,b]. Это самый эффективный, быстро сходящийся метод.
8. ПРИБЛИЖЕННОЕ РЕШЕНИЕ ОБЫКНОВЕННЫХ ДИФФЕРЕНЦИАЛЬНЫХ УРАВНЕНИЙ.
Обыкновенными дифференциальными уравнениями называются такие уравнения, которые содержат одну или несколько производных от искомой функции y=y(x)
F(x,y,y1,…,y(n)) = 0, где x-независимая переменная.
Решением дифференциального уравнения называется функция 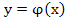 , которая после её подстановки в уравнение превращает его в торжество.
, которая после её подстановки в уравнение превращает его в торжество.
Некоторые методы решения известны по курсу дифференциальных уравнений. Для ряда уравнений первого порядка (с разделяющимися переменных однородных, линейных и др) удается получить решение в виде формул путем аналитических преобразований.
В большинстве случаев для решения дифференциальных уравнений используются приближенные методы, которые можно разделить на две группы:
1)аналитические методы, дающие решение в виде аналитического выражения;
2)численные методы, дающие приближенное решение в виде таблицы.
Рассмотрим перечисленные методы в виде следующих примеров.
8.1 МЕТОД ПОСЛЕДОВАТЕЛЬНОГО ДИФФЕРЕНЦИРОВАНИЯ.
Рассмотрим уравнение:
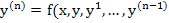
с начальными условиями 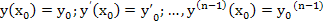 , где
, где 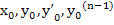 – заданные числа.
– заданные числа.
Предположим, что искомое решение y=f(x) может быть решено в ряд Тейлора по степеням разности (x-x0):
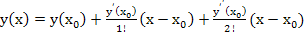 2
2 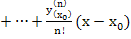 n+….
n+….
Начальные условия (8.2) дают нам значения y(k)(x0) при k=0,1,2,...,(n-1). Значения y(n)(x0) найдем из уравнения (8.1), подставляя (x-x0) и используя начальные условия (8.2):
y(n)(x0) = f(x0,y0,y'0,...,y0(n-1))
Значения y(n+1)(x0), y(n+2)(x0)... последовательно определяются дифференцированием уравнение (8.1) и подстановкой x=x0, y(k)(x0)=y0k (k – 0,1,2).
ПРИМЕР: Найти первые семь членов разложения в степенной ряд решения y=y(x) уравнения y''+0,1(y')2+(1+0,1x)y=0 с начальными условиями y(0)=1; y'(0)=2.
РЕШЕНИЕ: Решение уравнения ищем в виде ряда:
y(x)=y(0)+y'(0)x/1!+y''(0)x2/2!+...+y(n)(0)xn/n!...
Из начальных условий имеем y(0)=1, y'(0)=2. Для определения y''(0) разрешим данное уравнение относительно y'':
y''(0)= – 0,1(y')2 – (1+0,1x)y (8.3)
Используя начальные условия, получим
y''(0)= –0,1*4 – 1*1= –1,4
Дифференцируя по x левую и правую части уравнения (8.3)
y'''= – 0,2y'y'' – 0,1(xy'+y) – y',
y(4)= – 0,2(y'y'''+y''2) – 0,1(xy''+2y') – y'',
y(5)= – 0,2(y'y(4)+3y''y''') – 0,1(xy'''+3y'') – y''',
y(6)= – 0,2(y'y(5)+4y''y(4)+3y'''2) – 0,1(xy(4)+4y''' – y(4))
Подставляя начальные условия и значение y''(0), находим y'''(0)= – 1,54;
y(4)(0)= – 1,224; y(5) (0)=0,1768; y(6)(0)= – 0,7308. Таким образом, искомое приближенное решение запишется в виде: y(x) ≈ 1 + 2x – 0,7x2 – 0,2567x3 + 0,051x4 + 0,00147x5 – 0,00101x6.
8.2 МЕТОД ЭЙЛЕРА
Простейшими из численных методов решения дифференциальных уравнений является метод Эйлера, который основан на замене искомой функции многочленом первой степени, т.е. линейной экстраполяцией. Речь идет о нахождении значений функции в соседних точках аргумента x не между ними.
Выберем шаг h малым, чтобы для всех x между x0 и x1=x0+h значение функции y мало отличалось от линейной функции. Тогда на указанном интервале y = y0 + (x – x0)y' = y0 + (x –
| – x0)f'(x0y0), где y'0 = f'(x0,y0) – значение производной в точке х=х0 (см. Рисунок) Таким образом, кривая на этом участке заменяется отрезком прямой (касательной к кривой в начале участка). Для точки x1=x0+h, y1=y0+hy'0. Для точки x2=x1+h, y2=y1+hy'0. |
Продолжая таким же способом определять значения функции, убеждаемся, что метод Эйлера представляется в виде последовательного выполнения формул:
| (8.4) |
yk+1 = yk + ∆yk
ПРИМЕР
Решим методом Эйлера уравнения y' = x – y с начальным условием х0=0, у0=0 на отрезке [0,1] с шагом h=0,1.
Вычисления приведены в таблице.
Первая строка в столбцах 1 и 2 заполнена по начальным данным. Затем вычисляется у' по заданному уравнению (в столбце 4), затем ∆y = y'h – в столбце (4).
Столбец (5) содержит таблицу значений точного решения заданного уравнения.
| Из таблицы видно что при х=1 относительная ошибка метода Эйлера составляет δ=0,37 — 0,35/0,37*100%≈5,4% |
УТОЧНЕННЫЙ МЕТОД ЭЙЛЕРА
При том же объеме вычислительной работы дает более высокую точность.
Ранее мы считали подынтегральную функцию постоянной, равной её значению f(xk,yk) на левом конце участка. Более точное значение получится если полагать f(x,y(x)) равной значению в центре участка. Для этого надо брать двойной участок (xk-1,xk+1), заменив формулу
yk+1=yk+∆yk на yk+1=yk-1+2hy'k (8.5)
Эта формула и выражает уточненный метод Эйлера. Но в этом случае надо придерживать следующей последовательности действий:
| y1/2=y0+h/2y' y1=y0+hy' y2=y0+2hy' Далее расчёты вести по формуле (8.5). ПРИМЕР Для сравнения рассмотрим то же уравнение y' = x – y с начальными условиями x0=0, y0=0. Уточненный метод, как видно из таблицы дает более высокую точность относительная погрешность при х=1, у=0,370, а уточн 0,368. |
9.ВЫЧИСЛЕНИЕ ЗНАЧЕНИЙ ФУНКЦИИ.
9.1 ПОСТАНОВКА ЗАДАЧИ.
Постановка задачи.
При вычислении с помощью ЭВМ значений функции, заданных формулами, далеко не безразлично, в каком виде записана формула.
Предварительное вычисление всех нужных степеней аргумента х2, х3,... обычно не выгодно, так как требует довольно большого числа операций. При вычислении значений многочлена n-ой степени для получения степеней до хn требуется n–1 умножений. Кроме этого нужно ещё n умножений на коэффициенты, т.е. всего 2n–1 умножений к n сложений. Меньшего количества действий – n умножений и n сложений – требует вычисление многочлена по так называемой схеме Горнера, с которой мы сейчас познакомимся.
9.2 СХЕМА ГОРНЕРА ДЛЯ ВЫЧИСЛЕНИЯ
ЗНАЧЕНИЙ ПОЛИНОМА.
Из курса алгебры известна теорема Безу, которая утверждает, что остаток от деления многочлена f(x) на двучлен x-α равен значению многочлена при x=α, т.е. f(α).
Обозначив частное от деления полинома n-ой степени f(x) на x-α через φ(x), а остаток через bn, можно записать.
f(x)= (x-α)φ(x)+ bn, где bn=f(α) (9.1)
Если f(x)=a0xn+a1xn-1+...+an-1x+an; и φ(x)=b0xn-1+...+bn-2x+bn-1, то мы имеем тождество:
a0xn+a1xn-1+...+an-1x+an = (x-α) (b0xn-1+...+bn-2x+bn-1)+bn (9.2)
Раскрывая скобки в правой части тождества (9.2) и сравнивая коэффициенты в левой и правой частях тождества, находим:
a0=b0
a2=b2-αb1 ............. |
an-1=bn-1-αbn-2
an=bn-αbn-1
Равенство (9.3) перепишем в виде:
b0=a0
b2=a2+αb1 .............. |
bn-1=an-1+αbn-2
bn=an+αbn-1
С помощью полученных выражений можно вычислить последовательно все коэффициенты частного и остаток bn, равный f(α). Эта схема вычисления f(α) и называется схемой Горнера.
При ручном счёте (при нахождении одного значения многочлена) вычисления записывают с помощью схемы.
| a0 | a1 | a2 | ... | an-1 | an | |
| α | b0 | b1 | b2 | ... | bn-1 | bn |
Числа в нижней строке вычисляются последовательно слева направо с использованием равенств (9.4).
ПРИМЕР: Вычислить частное и остаток от деления многочлена x4+3x3+2x2+x+3, на (x-1,3). Пользуясь приведённой схемой, находим:
| –3 | |||||
| 1,3 | –3 +1*1,3=–1,7 | 2+(–1,7)*1,3= –0,21 | 1+(–0,21)*1,3=0,727 | 3+0,727*1,3=3,9451 |
Итак, частное есть многочлен x3-1,7x2-0,21x+0,727, а остаток, равный значению многочлена в точке х=1,3 есть 3,9451.
Таким образом, формулы (9.4) позволяют, не производя деления, определять коэффициенты частного φ(x), а также остаток bn = f(α). Практически вычисления осуществляются по следующей схеме, называемой схемой Горнера.
| + | a0 a1 a2 … an | α |
| b0α b1α … bn-1α | ||
| b0 b1 b2 … bn =f(α) |
ПРИМЕР вычислить значение полинома:
P(x) = 3x3 + 2x2 – 5x +7 при х = 3.
РЕШЕНИЕ Составляем схему Горнера:
| + | 3 2 –5 7 | |
| 9 33 84 | ||
| 3 11 28 91=f(3) |
Итак, частное есть φ(x) = 3x2 + 11x + 28 и остаток равный значению полинома в точке x=3 есть 91.
Если в формулах (9.4) подставить каждую предыдущую формулу в последующую, то получатся такие равенства:
| b1 = a1 + αa0 b2 = a2 + α(a1 + αa0) b3 = a3 + α(a2 + α(a1 + αa0)) ……………………………... |
Дойдя до последней формулы и переписав правую часть в обратном порядке, получим:
bn = f(α) = (… ((a0α + a1)α + a2)α + … + an-1)α + an
Таким образом, для вычисления многочлена
f(x) = a0xn + a1xn-1 + … + an-1x + an
его следует представить в виде:
f(x) = (… ((a0x + a1)x + a2)x + … + an-1)x + an.
ПРИМЕР. Составить таблицу значений многочлена x4 – 3x3 + 2x2 + x +3 для значений x от 1 до 2 с шагом 0,2.
РЕШЕНИЕ. Представим заданный многочлен в виде:
(((x – 3)x + 2)x + 1)x + 3
Расписку для выполнения вычислений вручную осуществим в виде таблицы:
| (1) | (2) | (3) | (4) | (5) |
| x | (1) – 3 | (2) ∙ (1) + 2 | (3) ∙ (1) + 1 | (4) ∙ (1) + 3 |
| 1,0 1,2 1,4 1,6 1,8 2,0 | – 2,0 –1,8 –1,6 –1,4 –1,2 –1,0 | 0,00 –0,16 –0,24 –0,24 –0,16 | 1,000 0,808 0,664 0,616 0,712 1,000 | 4,0000 3,9696 3,9296 3,9856 4,2816 5,0000 |
9.3 ОПРЕДЕЛЕНИЕ ГРАНИЦ ДЕЙСТВИТЕЛЬНЫХ КОРНЕЙ
ПОЛИНОМА ПО СХЕМЕ ГОРНЕРА.
Положим, что при x = β (β=0) все коэффициенты bi в схеме Горнера неотрицательны, причем первый коэффициент положителен, т.е.
b0 = a0 > 0 и bi>0 (i=1,2,…,n)
Тогда можно утверждать, что все действительных корней xk полинома f(x) расположены не правее β, т.е. xk ≤ β (см. рис.)
| В самом деле, так как f(x) = (b0xn-1 + … + bn-1)(x – β) + bn, |
то при любом x>β будем иметь f(x)>0. Таким образом, имеем верхнюю оценку для действительных корней xk полинома.
Для получения нижней оценки корней xk составляем полином
(–1)nf(–x) = a0xn – a1xn-1 + … + (–1)nan
Дата публикования: 2014-11-18; Прочитано: 371 | Нарушение авторского права страницы | Мы поможем в написании вашей работы!