 |
Главная Случайная страница Контакты | Мы поможем в написании вашей работы! | |
Федеральное государственное бюджетное образовательное учреждение высшего профессионального образования 3 страница
|
|
Эту формулу можно записать и для значения разности в узле xi:
∆kyi = yk+1 – kyk+i-1 + 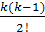 yk+i-2 + … + (–1)kyi
yk+i-2 + … + (–1)kyi
4.3 ИНТЕРПОЛЯЦИОННАЯ ФОРМУЛА НЬЮТОНА.
Перейдем к построению интерполяционного многочлена Ньютона. Этот многочлен будем искать в следующем виде:
N(x) = a0 + a1(x – x0) + a2(x – x0)(x – x1)+ … + an(x – x0)(x – x1)…(x – xn-1) (4.2)
График многочлена должен проходить через заданные узлы, т.е. N(xi) = yi (i=0,1,2,…n). Эти условия используем для нахождения коэффициентов многочлена; учитывая, что xi – xi-1=h:
N(x0) = a0 = y0
N(x1) = a0 + a1(x1 – x0) = a0 + a1h = y1
N(x2) = a0 + a1(x2 – x0) + a2(x2 – x0)(x2 – x1) = a0 + a1h + 2a2h2 = y2
.... … … … … … …
Отсюда найдем коэффициенты:
a0 = y0; a1 = 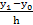 =
= 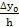 ;
;
a2 = 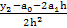 =
= 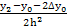 =
= 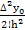
Аналогично можно найти и другие коэффициенты. Общая формула имеет вид:
ak = 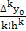 k = 0, 1, …, n.
k = 0, 1, …, n.
Подставляя эти выражегия в формулу (4.2), получаем следующий вид интерполяционного многочлена Ньютона:
N(x) = y0 + 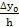 (x – x0) +
(x – x0) + 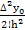 (x – x0) (x – x1) + …
(x – x0) (x – x1) + …
+ 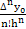 (x – x0) (x – x1)…(x – xn-1) (4.3)
(x – x0) (x – x1)…(x – xn-1) (4.3)
Конечные разности ∆ky0 вычисляются по формуле (4.1).
Формулу (4.3) часто записывают в другом виде. Для этого введем переменную
q = 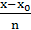 , тогда
, тогда
x = x0 + qh, 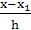 =
= 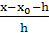 = q – 1,
= q – 1,
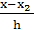 = q – 2, …,
= q – 2, …, 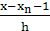 = q – n + 1
= q – n + 1
Тогда формула (4.3) примет вид:
N(x) = N(x0 + qh) = y0 + q∆y0 + 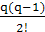 ∆2y0 + …+
∆2y0 + …+ 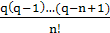 ∆ny0 (4.4)
∆ny0 (4.4)
Полученное выражение называется первым интерполяционным многочленом Ньютона для интерполирования вперед. Оно может интерполировать данную функцию y=f(x) на всем отрезке изменения аргумента [x0, xn] слева направо. С точки зрения повышения точности расчетов целесообразно произвести интерполяцию этой функции в интервале аргумента [x0, xn] справа налево. В этом случае
q = 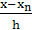 , т.е. q<0
, т.е. q<0
тогда интерполяционный многочлен Ньютона можно получить в виде:
N(x) = N(xn + qh) = yn + q∆yn-1 +  ∆2yn-2 + … +
∆2yn-2 + … + 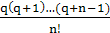 ∆ny0 (4.5)
∆ny0 (4.5)
Полученная формула называется вторым интерполяционным многочленом Ньютона для интерполирования назад.
Из первого полинома Ньютона (4.4) при n=1 имеем линейную интерполяцию
N(x) = y0 + q∆y0
При n=2 – квадратичную N(x) = y0 + q∆y0 + 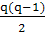 ∆2y0.
∆2y0.
На практике используются полиномы 1, 2 и 3 степени.
ПРИМЕР 4.2
Применяя I и II формулы интерполяционного многочлена Ньютона, вычислить в точке x = 0,1 значение функции y = f(x), заданной таблицей:
| x | y | ∆y | ∆2y | ∆3y | ∆4y | ∆5y |
| 0,2 0,4 0,6 0,8 1,0 | 1,272 4,465 5,644 5,809 3,961 2,101 | 3,193 1,179 0,165 –1,848 –1,860 | –2,014 –1,014 –2,013 –0,012 | 1,000 –0,999 2,001 | –1,999 3,000 | 4,999 |
Процесс вычислений удобно свести в ту же таблицу. Каждая последующая конечная разность получается путем вычитания в предыдущей колонке верхней строки из нижней.
При x=0,1 имеем q = 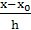 =
= 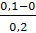 = 0,5
= 0,5
Проводим вычисления по формуле (4.4)
f(0,1) ≈ N(0,1) = 1,272 + 0,5 ∙ 3,193 + 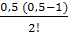 (–2,014) +
(–2,014) + 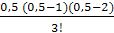 ∙ 1,000 + +
∙ 1,000 + + 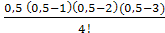 ∙ (–1,999) +
∙ (–1,999) + 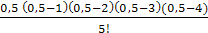 ∙ 4,999 = 1,272 + 1,597 + +0,2518 + +0,06249 + 0,07809 + 0,1367 = 3,398.
∙ 4,999 = 1,272 + 1,597 + +0,2518 + +0,06249 + 0,07809 + 0,1367 = 3,398.
Для сравнения проведем аналогичные вычисления по формуле (4.5). В этом случае:
q = 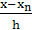 =
= 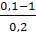 = –4,5.
= –4,5.
Тогда
f(0,1) ≈ N(0,1) = 2,101 – 4,5 ∙ (–1,860) + 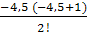 ∙ (–0,012) +
∙ (–0,012) +  ∙2,001 +r w:top="1134" w:right="850" w:bottom="1134" w:left="1701" w:header="720" w:footer="720" w:gutter="0"/><w:cols w:space="720"/></w:sectPr></w:body></w:wordDocument>">
∙2,001 +r w:top="1134" w:right="850" w:bottom="1134" w:left="1701" w:header="720" w:footer="720" w:gutter="0"/><w:cols w:space="720"/></w:sectPr></w:body></w:wordDocument>"> 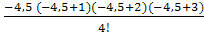 ∙ 3,000 +
∙ 3,000 + 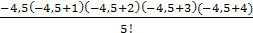 ∙ 4,999 = =2,101 + 8,370 – 0,09450 + 13,13 + 7,383 – 1,231 = 3,402
∙ 4,999 = =2,101 + 8,370 – 0,09450 + 13,13 + 7,383 – 1,231 = 3,402
Видно, что здесь происходит незначительная потеря точности.
ВЫПОЛНИТЬ САМОСТОЯТЕЛЬНО
ЗАДАНИЕ 4
1. Вычислить значение функции с помощью первой интерполяционной формулы Ньютона при значении аргумента x*.
2. Вычислить значение функции с помощью интерполяционной формулы Лагранжа при значении аргумента x*, приняв n=3. Исходные числовые данные приведены в таблице 4.
ТАБЛИЦА 4
| 0,1,2 | 3,4,5,6 | 7,8,9 | |||||||
| x | y | x* | x | y | x* | x | y | x* | |
| 0, | 0,0872 0,1736 0,2588 0,3420 0,4226 | 0,1219 0,1736 0,2250 0,2756 0,3256 | 0,1564 0,2250 0,2924 0,3584 0,4226 | ||||||
| 2, | 0,1045 0,2079 0,3090 0,4067 0,4226 | 0,1908 0,2588 0,3256 0,3907 0,4540 | 0,1392 0,2250 0,3090 0,3907 0,4695 | ||||||
| 4, | 0,1736 0,2419 0,2424 0,3584 0,4226 | 0,0175 0,0872 0,1564 0,2250 0,2924 | 0,0349 0,1219 0,2079 0,2924 0,3746 | ||||||
| 6, | 0,0523 0,1392 0,2250 0,3090 0,3907 | 0,0698 0,1392 0,2079 0,2756 0,3420 | 0,2079 0,2924 0,3746 0,4540 0,5299 | ||||||
| 8, | 0,2419 0,3090 0,3746 0,4384 0,5000 | 0,2588 0,3256 0,3907 0,4540 0,5150 | 0,2756 0,3420 0,4067 0,4695 0,5299 |
ПРИМЕР 1.
С помощью интерполяционной формулы Ньютона вычислить в точке x*=19 значение функции, заданной в таблице 4.
РЕШЕНИЕ. Составим таблицу конечных разностей.
| i | x | y | ∆y | ∆2y | ∆3y | ∆4y |
| 0,2924 0,3907 0,4848 0,5736 0,6541 | 0,0983 0,0941 0,0888 0,0805 | –0,0042 –0,0095 –0,0083 | –0,0053 0,0012 | 0,0065 |
∆y0 = y1 – y0 = 0,3907 – 0,2924 = 0,0983
∆y1 = y2 – y1 = 0,4848 – 0,3907 = 0,0941
∆2y2 = ∆y1 - ∆y0 = 0,0941 – 0,0983 = –0,0042
и так далее.
По первой интерполяционной формуле Ньютона (4.4), ограничиваясь конечными разностями четвертого порядка, имеем:
N(x) = y0 + q∆y0 + 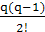 ∆2y0 +
∆2y0 +  ∆2y0 +
∆2y0 + 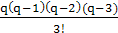 ∆3y0 + +
∆3y0 + + 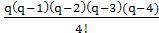 ∆3y0
∆3y0
Т.к. x*=19, h=6 и x0=0,2924, то q= 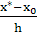 =
= 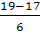 = 0,17
= 0,17
Получим:
N(0,1) = 0,2924 + 0,17 ∙ 0,0983 + 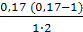 ∙ (–0,0042) +
∙ (–0,0042) + 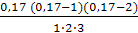 ∙(–0,0053) +
∙(–0,0053) + 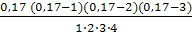 ∙ 0,005 = 0,309164.
∙ 0,005 = 0,309164.
Таким образом, при x*=19 значение функции N(x*) = 0,309164.
4.4 ИНТЕРПОЛЯЦИОННАЯ ФОРМУЛА
ЛАГРАНЖА.
В случае непостоянного шага интерполирования
xi – xi-1 = hi ≠ const при i=1,2,…,n
используется так называемая интерполяционная формула Лагранжа.
| Пусть на отрезке [a,b] даны n+1 значений аргумента x0, x1, x2, …, xn и для функции y=f(x) известны соответствующие значения f(x0)=y0, f(x1)=y1, …, f(xn)=yn Строится поленом Ln(x), имеющий в заданных узлах x0, x1,..., xn те же значения, что и функция f(x), т.е. такой, что Ln(xi) = yi (i=0, 1, …, n) Такой поленом имеет вид: |
|
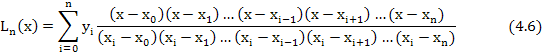
Это и есть интерполяционная формула Лагранжа.
4.5 ЛИНЕЙНАЯ И КВАДРАТИЧНАЯ
ИНТЕРПОЛЯЦИЯ.
Рассмотрим два частных случая интерполяционного полинома Лагранжа.
При n=1 мы имеем две точки – (x0,x1), и получим из формулы (4.6) уравнение прямой y=L1(x), проходящей через эти точки
y=L1(x)= 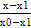 y0 +
y0 + 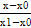 y1
y1
При x0=a, x1=b получим y = 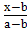 y0 +
y0 + 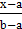 y1
y1
При n=2 получим уравнение параболы, проходящей через 3 точки x0=a, x1=b, x2=c
L2(x) = 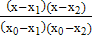 y0 +
y0 + 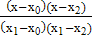 y1 +
y1 + 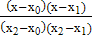 y2 =
y2 = 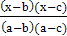 y0 +
y0 +  y1
y1 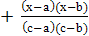 y2
y2
Пример 1 Для функции y=sinπx построить интерполяционный полином Лагранжа, выбрав узлы x0=0, x1=  , x2=
, x2=  .
.
Решение Вычислим соответствующие значения функции y0=0, y1= sin  =
=  , y2= sin
, y2= sin  =1
=1
Применяя формулу (4.6), получим:
L2(x) = 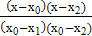 y0 +
y0 + 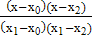 y1 +
y1 + 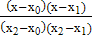 y2 =
y2 = 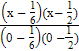 ∙ 0 +
∙ 0 + 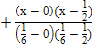 ∙
∙  +
+ 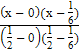 ∙ 1 =
∙ 1 =  x – 3x2
x – 3x2
Пример 2 С помощью интерполяционной формулы Лагранжа вычислить значение функции при значении аргумента x*=323.5, приняв n=3. В соответствии с вариантом выбрать исходные данные из таблицы 4 индивидуального задания.
| i | x | y |
| 321,0 | 2,50651 | |
| 322,8 | 2,50893 | |
| 324,2 | 2,51081 | |
| 325,0 | 2,51188 |
Решение Подставим значения x*, xi и yi в интерполяционную формулу Лагранжа (4.6)
L(x*) = y0 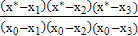 + y1
+ y1 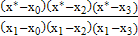 + y2
+ y2 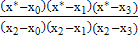 +
+ 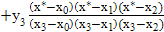
Получим:
L(323,5) = 2,50651 ∙  + 2,50893 ∙
+ 2,50893 ∙ 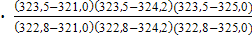 + 2,51081 ∙
+ 2,51081 ∙ 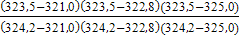 +2,51188∙
+2,51188∙ 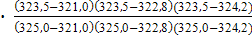 = –0,07996 + 1,18794 + 1,83897 – 0,43708 =2,50987
= –0,07996 + 1,18794 + 1,83897 – 0,43708 =2,50987
Таким образом, в точке x*=323,5 функция f(x*)=2,50987.
5. ОПРЕДЕЛЕНИЕ ПАРАМЕТРОВ ЭМПИРИЧЕСКИХ
ФОРМУЛ.
5.1 ПОДБОР ЭМПИРИЧЕСКИХ ФОРМУЛ.
Пусть при обработке экспериментальных данных получена таблица данных
| x0 | x1 | x2 | … | xn |
| y0 | y1 | y2 | … | yn |
Необходимо построить зависимость y=f(x), приближенно отображающую эти данные.
Вид эмпирической формулы может быть произвольным. В этом случае предпочтение отдается наиболее простым формулам.
Более строгий выбор эмпирической формулы производится на основе анализа i-ых конечных разностей по данным таблицы. Если расстояние между узлами ∆xi = xi – xi-1 = const, то:
1) при условии ∆yi≈const следует в качестве эмпирической формулы использовать линейную зависимость
y = ax + b;
2) при ∆2yi≈const – квадратичную
y = ax2 + bx + c;
3) при ∆3yi≈const – кубическую
y = ax3 + bx2 + cx + d;
и т.д.
рассмотрим несколько методов определения параметров эмпирических формул.
5.2 МЕТОД ВЫБРАННЫХ ТОЧЕК.
Пусть получена некоторая таблица данных y=f(x). На плоскости XOY нанесем эти точки
| (*), а затем проведем кривую φ(x), примыкающую к этим точкам, и выберем на этой линии точки (◦). Число выбранных точек должно быть равным количеству исходных параметров. Координаты этих точек измеряются и используются для вычисления коэффициентов эмпирической зависимости. |
Если используется эмпирическая зависимость
φ(x) = a0 + a1x + a2x2 + … + anxn
то для вычисления n+1 коэффициентов ai нужно задать n+1 точку. В результате получим систему n+1 линейных уравнений
a0+a1x0+a2 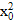 +…+an
+…+an 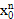 =y0
=y0
a0+a1x1+a2 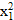 +…+an
+…+an 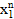 =y1
=y1
… … … …
a0+a1xn+a2 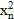 +…+an
+…+an 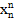 =yn
=yn
т.к. значения xi и yi (i=0,1,2,…,n) известны.
5.3 МЕТОД СРЕДНИХ.
Этот метод заключается в том, что параметры ai эмпирической зависимости
y = φ(xi;a0,a1,…,an)
определяются из условия равенства нулю суммы отклонений ее от табличных значений y во всех точках xi
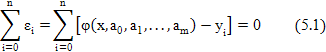
Поскольку из уравнения (5.1) нельзя однозначно определить n+1 коэффициент эмпирической формулы φ(x,ai), то уравнение (5.1) путем группировки отклонений εi, разбивается на систему, состоящую из m+1 уравнений. Например:
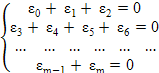
Решая систему (5.2), находим неизвестные параметры ai.
Пример. Рассмотрим торможение движущегося тела.
| t,с | ||||||
| S,м |
Считая движение равнозамедленным, найти приближенные значения скорости V0 и ускорения a.
Решение. Согласно физическому смыслу уравнение движения имеет вид следующей эмпирической формулы:
x = At2 +Bt + C
Из таблицы видно, что при t=0 x=0, следовательно, C=0, тогда:
x = At2 + Bt
Воспользуемся методом средних и запишем уравнения для всех точек, кроме начальной:
ε1+ ε2+ ε3+ ε4+ ε5=0
Путем расщепления этого уравнения запишем систему двух уравнений:
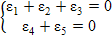
Используя выражение x = At2 + Bt и табличные данные, получим:
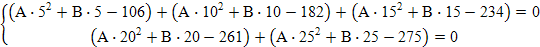
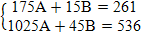
A = –0,30; B = 39,07
Формула, дающая приближенную связь между пройденным расстоянием и времени имеет вид:
x = –0,30t2 + 39,07t
Сравнивая это уравнение с уравнением
x = 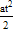 + V0t,
+ V0t,
получим:
a = 2A = –0,60 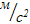 , V0 = 39,07
, V0 = 39,07 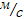 .
.
5.4 МЕТОД СРЕДНИХ.
Запишем сумму квадратов отклонений для всех точек x0, x1, …, xn
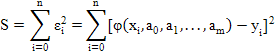
Поскольку здесь параметры эмпирической формулы a0, a1, …, am выступают в роли независимых переменных функции S, то ее минимум найдем, приравнивая нулю частные производные по этим параметрам:
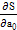 = 0;
= 0; 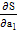 = 0; …; s w:ascii="Times New Roman" w:h-ansi="Times New Roman"/><wx:font wx:val="Times New Roman"/><w:sz w:val="24"/><w:sz-cs w:val="24"/><w:lang w:val="EN-US"/></w:rPr><m:t>m</m:t></m:r></m:sub></m:sSub></m:den></m:f></m:oMath></m:oMathPara></w:p><w:sectPr wsp:rsidR="00000000"><w:pgSz w:w="12240" w:h="15840"/><w:pgMar w:top="1134" w:right="850" w:bottom="1134" w:left="1701" w:header="720" w:footer="720" w:gutter="0"/><w:cols w:space="720"/></w:sectPr></w:body></w:wordDocument>">
= 0; …; s w:ascii="Times New Roman" w:h-ansi="Times New Roman"/><wx:font wx:val="Times New Roman"/><w:sz w:val="24"/><w:sz-cs w:val="24"/><w:lang w:val="EN-US"/></w:rPr><m:t>m</m:t></m:r></m:sub></m:sSub></m:den></m:f></m:oMath></m:oMathPara></w:p><w:sectPr wsp:rsidR="00000000"><w:pgSz w:w="12240" w:h="15840"/><w:pgMar w:top="1134" w:right="850" w:bottom="1134" w:left="1701" w:header="720" w:footer="720" w:gutter="0"/><w:cols w:space="720"/></w:sectPr></w:body></w:wordDocument>"> 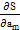 = 0
= 0
Это и есть система уравнений для определения коэффициентов a0, a1, a2, …
Рассмотрим применение этого метода на примере эмпирической функции:
φ(x) = a0 + a1x + a2x2 + … + amxm
Тогда:
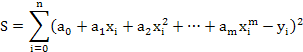
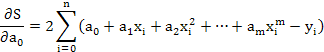
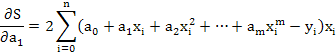
…………………………………………………………….
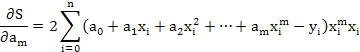
Приравниваем эти выражения нулю и, собирая коэффициенты a0, a1, …, am, получаем следующую систему:
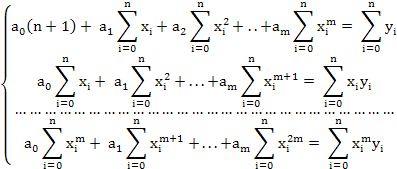
Решая эту систему, получим искомые параметры эмпирической формулы. Систему можно записать в более компактном виде.
Введём обозначения:
y m:val="p"/></m:rPr><w:rPr><w:rFonts w:ascii="Cambria Math" w:h-ansi="Cambria Math"/><wx:font wx:val="Cambria Math"/><w:sz-cs w:val="24"/><w:lang w:val="EN-US"/></w:rPr><m:t> (5.3)</m:t></m:r></m:oMath></m:oMathPara></w:p><w:sectPr wsp:rsidR="00000000"><w:pgSz w:w="12240" w:h="15840"/><w:pgMar w:top="1134" w:right="850" w:bottom="1134" w:left="1701" w:header="720" w:footer="720" w:gutter="0"/><w:cols w:space="720"/></w:sectPr></w:body></w:wordDocument>"> 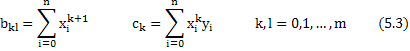
Получим:
b00a0 + b01a1 + … + b0mam = c0
Дата публикования: 2014-11-18; Прочитано: 350 | Нарушение авторского права страницы | Мы поможем в написании вашей работы!
