Свойства операций симметрии

Из рассмотрения операций симметрии вытекают следующие свойства.

1. Если кристаллическая структура характеризуется определенным набором элементов симметрии, то результатом следующих одно за другим преобразований симметрии будет преобразование симметрии, входящее в этот набор.

Пусть S и R – операции симметрии.

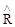Подействовав на функцию сначала оператором , получим тождественное (симметричное) состояние, т. е.

,

где – оператор идентичной операции, или элемент тождественного преобразования.

Подействуем на результат оператором

.

Можно результат произведения двух операций симметрии сопоставить еще одной операцией симметрии 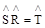, тогда

.

2. Обязательно в совокупности элементов симметрии, свойственной данному кристаллу, существует идентичное преобразование симметрии , оставляющее рассматриваемое свойство объекта неизменным

.

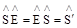3. Для каждого преобразования симметрии, описываемого оператором , можно найти обратное преобразование, описываемое оператором ; например, поворот на 120⁰ по часовой стрелке, затем поворот на 120⁰ против часовой стрелки.

4. Если действовать последовательно преобразованиям симметрии, то конечный результат действия определяется лишь последовательностью проведения операций симметрии

.

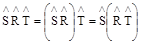Эти рассмотренные свойства можно обобщить.

Абстрактной группой G называется множество элементов, удовлетворяющее следующим условиям или аксиомам:

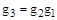1. Для всех элементов группы определена операция умножения, т. е. для каждой пары элементов, взятых в определенной последовательности, определяется действие умножения, в результате которого произведению сопоставляется определенный элемент того же множества. Если элемент g₁ принадлежит группе , и , то и 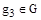. В общем случае . Группы, для которых равенство выполняется для всех элементов, называется «абелевыми» или коммутативными.

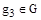2. Для элементов абелевых групп имеет место сочетательный закон, т. е. если и , и , то

.

3. Множества должны содержать единичный элемент или элемент тождественного преобразования, для которого свойственно Еg = gE = g.

4. Для любого элемента группы найдется элемент 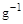, также принадлежащий группе и называемый обратным g, для которого

.

Очевидно, что совокупность элементов симметрии в кристаллах обладает вышеперечисленными свойствами. Эта совокупность носит название точечной группы кристалла (точечной, поскольку при действии элементов симметрии, по крайней мере, одна точка кристалла остается неподвижной). Все многообразие кристаллических структур описывается 32 точечными группами.

Представление о точечных группах находит применение в квантовой механике и физике твердого тела для описания симметрии внешней формы кристалла, симметрии физических свойств кристалла, описываемых тензорами различного ранга.

Точечные группы определяют анизотропию свойств кристалла. Чем беднее элементами симметрии точечная группа кристалла, тем более анизотропен кристалл. Поскольку физические свойства кристаллов описываются тензорами различного ранга, значение точечной группы кристалла позволяет заранее оценить, какое число независимых величин (компонент тензора) определяют соответствующее свойство данного кристалла (электропроводность, упругость). Симметрия направлений, а поэтому и симметрия макроскопических свойств кристалла определяются совокупностью его осей и плоскостей симметрии.

Трансляционная симметрия определяет важнейшие свойства кристаллов, такие, как зонный характер энергетического спектра электронов. Трансляционная симметрия характеризует пространственную группу кристалла, она включает в себя элементы точечной группы, плюс винтовые оси и плоскости скользящего отражения.