Формула Стирлинга

Для успешного применения радиального признака Коши полезно знать асимптотическую формулу для n!, выведенную Стирлингом

при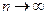

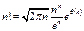, где .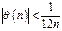

(Без доказательства.)

Примеры.

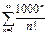
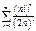
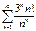
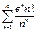
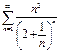
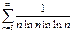
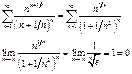(ряд расходится по необходимому §11. Знакопеременные ряды.

Определение. Пусть " a_n ³0, тогда ряд 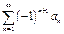- знакопеременный ряд.

Теорема Лейбница. Есл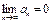и и 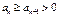, то знакочередующийся ряд 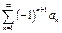сходится. При этом " n 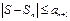- модуль n -ого остатка ряда не превышает модуля следующего члена ряда.

Доказательство.

Рассмотрим частичные суммы ряда четного порядка

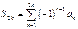
Их можно записать в виде

,

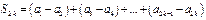здесь каждая скобка неотрицательна, т.о. 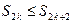Þ последовательность частичных сумм четного порядка не убывает.

Заметим, что ту же последовательность можно записать и так

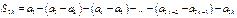Þ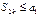

Т.е. неубывающая последовательность ограничена сверху Þ она сходится,

.

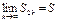Покажем, что последовательность частичных сумм нечетного порядка стремится к тому же пределу. Действительно,

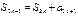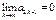и Þ

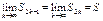
Отметим, что для знакопеременного ряда справедливо S_2k £ S £ S_2k+1. Так как { S_2k } – неубывающая последовательность, а { S_2k+1 } – невозрастающая последовательность. Обе сходятся к своей верхней (нижней) грани.

Þ S - S_2k £ S_2k+1 - S_2k = a _2k+1

и S_2k-1 -S £ S_2k-1 - S_2k = a _2k

Þ .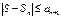

Пример.

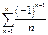- сходится в силу признака Лейбница. И его сумма .

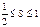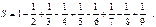
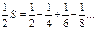
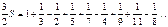
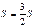Þ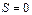

Причина противоречия состоит в том, что не все свойства сумм переносятся на ряды. В частности, слагаемые можно переставлять только в абсолютно сходящихся рядах.