 |
Главная Случайная страница Контакты | Мы поможем в написании вашей работы! | |
А) Непосредственное моделирование
|
|
Если 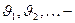 последовательность независимых случайных величин с распределением Бернулли, то есть
последовательность независимых случайных величин с распределением Бернулли, то есть 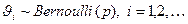 , тогда случайная величина
, тогда случайная величина 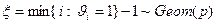 , где
, где 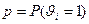
Алгоритм генерирования 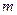 значений случайной величины
значений случайной величины 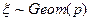 :
:
1. Задаем 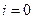 и
и 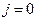 .
.
2. Генерируют значение случайной величины 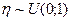 :
: 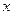 .
.
3. Если 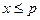 , то
, то 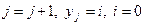 . В противном случае
. В противном случае 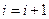 .
.
4. Если 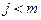 возвращаемся к шагу 2. В противном случае переход к шагу 5.
возвращаемся к шагу 2. В противном случае переход к шагу 5.
5. Полученная последовательность 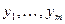 является выборкой объема
является выборкой объема 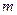 значений случайной величины имеющей геометрическое распределение.
значений случайной величины имеющей геометрическое распределение.
б) Моделирование с помощью показательного распределения. Пусть 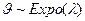 , тогда
, тогда
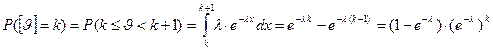
и следовательно, случайная величина 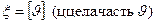 имеет геометрическое распределение с параметром
имеет геометрическое распределение с параметром 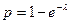 . Поэтому если взять
. Поэтому если взять 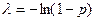 , то
, то 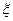 будет иметь нужное нам распределение. Следовательно, если
будет иметь нужное нам распределение. Следовательно, если 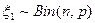 и
и 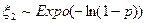 , то
, то 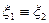 . Для построения алгоритма необходимо выполнить последовательность действий примера из пункта 4.6.2.
. Для построения алгоритма необходимо выполнить последовательность действий примера из пункта 4.6.2.
4.9.4. Моделирование гамма - распределения. Непрерывная случайная величина 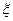 имеет гамма - распределение с параметрами
имеет гамма - распределение с параметрами 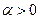 и
и 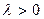 , если она имеет функцию плотности вероятностей вида
, если она имеет функцию плотности вероятностей вида
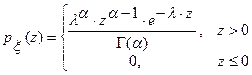 ,
,
Где 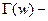 гамма-функция Эйлера, для
гамма-функция Эйлера, для  и
и 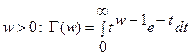 .
.
Свойства гамма - функции: 1) 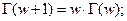 2)
2) 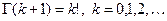 . Обозначение
. Обозначение 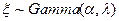 .
.
Частный случай гамма – распределения это распределение Эрланга 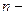 го порядка, когда
го порядка, когда 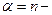 целое положительное число. Непрерывная случайная величина
целое положительное число. Непрерывная случайная величина 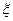 имеет распределение Эрланга
имеет распределение Эрланга 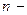 го порядка с параметрами
го порядка с параметрами 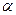 и
и 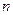 , если она имеет функцию плотности вероятностей вида
, если она имеет функцию плотности вероятностей вида
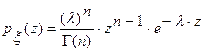 ,
,
Где 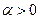 ,
, 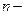 целое число.
целое число.
Теорема 7. Случайная величина 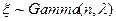 и ее плотность вероятностей равна
и ее плотность вероятностей равна
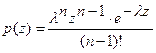 .
.
Тогда 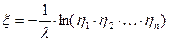 , где
, где 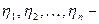 независимые случайные величины и
независимые случайные величины и 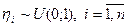 .
.
Доказательство. Доказательство проведем по индукции. При 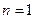 получаем
получаем 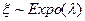 и тогда согласно пункта 4.6.2 имеем, что
и тогда согласно пункта 4.6.2 имеем, что 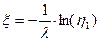 . Пусть утверждение теоремы верно при
. Пусть утверждение теоремы верно при 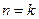 . Докажем, что оно также верно и для
. Докажем, что оно также верно и для 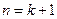 . Обозначим
. Обозначим 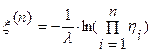 ,
, 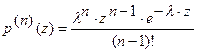 и
и 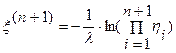 ,
, 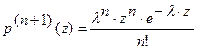 тогда
тогда 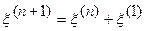 .
.
Воспользуемся правилом композиции плотностей независимых слагаемых
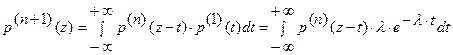
Воспользуемся индуктивным допущением
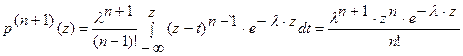
Теорема доказана.
Следствие. Пусть 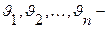 независимые случайные величины,
независимые случайные величины, 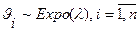 . Тогда
. Тогда 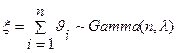 .
.
Примечание: Распределение Эрланга используется в теории массового обслуживания, описывая в ряде ситуаций распределение времен обслуживания.
4.9.5. Распределение Вейбулла. Непрерывная случайная величина 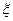 имеет распределение Вейбулла с параметрами
имеет распределение Вейбулла с параметрами 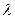 и
и 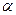 , если она имеет функцию распределения
, если она имеет функцию распределения 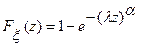 , где
, где 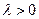 и
и 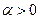 . Обозначают
. Обозначают 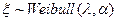 .
.
Для построения алгоритма моделирования, очевидно, что проще всего воспользоваться методом обратной функции.
Примечание: Распределение Вейбулла находит применение в статистической теории надежности при описании распределений времени без отказной работы.
4.9.6. Логнормальное распределение. Непрерывная случайная величина 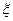 имеет логнормальное распределение с параметрами
имеет логнормальное распределение с параметрами  и
и 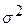 , если она имеет функцию плотности вероятностей вида
, если она имеет функцию плотности вероятностей вида
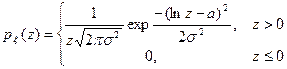 ,
,
где 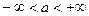 и
и 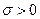 . Обозначают
. Обозначают 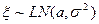 .
.
Воспользуемся свойством логнормального распределения – если 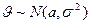 , то
, то 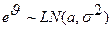 , следовательно
, следовательно 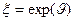 .
.
Алгоритм генерирования 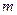 значений случайной величины
значений случайной величины 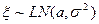 :
:
1. Генерируют 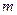 значение случайной величины
значение случайной величины 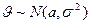 :
: 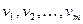 . Для этого можно использовать любой из алгоритмов описанных в пункте 4.7.
. Для этого можно использовать любой из алгоритмов описанных в пункте 4.7.
2. Проводят вычисления значений 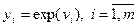 .
.
3. Полученная последовательность 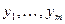 является выборкой объема
является выборкой объема 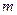 значений случайной величины имеющей логнормальное распределение с заданными параметрами.
значений случайной величины имеющей логнормальное распределение с заданными параметрами.
Примечание: Логнормальное распределение используется в моделях дробления частиц, в моделях роста.
4.9.7. Моделирование многомерного нормального распределения. Функция плотности вероятностей случайной величины 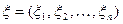 многомерного нормального распределения определяется как
многомерного нормального распределения определяется как
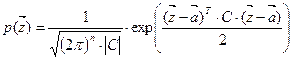 ,
,
для любого вектора 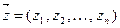 в
в 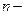 мерном вещественном пространстве;
мерном вещественном пространстве; 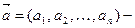 вектор средних значений, где
вектор средних значений, где 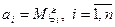 ;
; 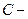 ковариационная матрица. Многомерное нормальное распределение обозначают как
ковариационная матрица. Многомерное нормальное распределение обозначают как 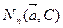 . Матрица
. Матрица 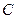 является симметричной и положительно определенной, и используя разложение Холецкого ее можно представить в виде
является симметричной и положительно определенной, и используя разложение Холецкого ее можно представить в виде 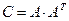 , где
, где 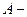 нижнетреугольная матрица.
нижнетреугольная матрица.
Алгоритм моделирования случайной величины 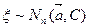 .
.
1. 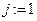 .
.
2. Генерируется по алгоритму пункта 4.7.1 вектор 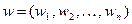 значений
значений 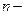 независимых и одинаково распределенных случайных величин
независимых и одинаково распределенных случайных величин 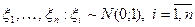 .
.
3. Вычисляют 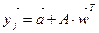 и
и 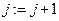 .
.
4. Если 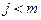 , то возвращаемся к пункту 2. В противном случае переходим к пункту 5.
, то возвращаемся к пункту 2. В противном случае переходим к пункту 5.
5. 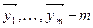 значений случайной величины
значений случайной величины 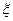 .
.
4.9.8. Моделирование многомерного логнормального распределения. Определим многомерное логнормальное распределение через его отношение к многомерному нормальному распределению: случайная величина 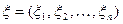 имеет логнормальное многомерное распределение, когда случайная величина
имеет логнормальное многомерное распределение, когда случайная величина 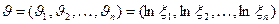 имеет многомерное нормальное распределение
имеет многомерное нормальное распределение 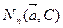 . Тогда случайный вектор многомерного логнормального распределения можно представить как
. Тогда случайный вектор многомерного логнормального распределения можно представить как 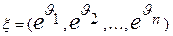 , где
, где 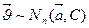 . Принятое обозначение
. Принятое обозначение 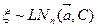
Алгоритм генерирования случайной величины 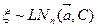 .
.
1. По алгоритму пункта 4.9.7 генерируем многомерную случайную величину 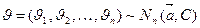 .
.
2. Возвращаем случайную величину 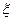 :
:
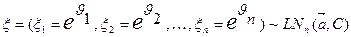
Дата публикования: 2014-11-18; Прочитано: 666 | Нарушение авторского права страницы | Мы поможем в написании вашей работы!
