Применение дискретного операционного исчисления

Преимуществом дискретного операционного исчисления является то, что его можно использовать как численный метод, а не только как символьные преобразования. При этом оно опирается на хорошо отработанную технологию матричных преобразований и алгоритмов. Например, можно использовать такую популярную программу технических вычислений, как MATLAB.

Спектр возможных приложений достаточно широк. Дискретное операционное исчисление можно использовать для численного (либо символьного) решения конечно-разностных уравнений. Рассмотрим следующий пример. Решим разностное (рекуррентное) уравнение при нулевых начальных условиях

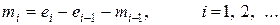
где

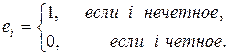
Для этого перейдем к матричному представлению этого уравнения, используя теорему 11.3:

,

где .

Отсюда следует

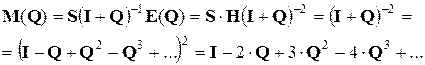
Таким образом

.

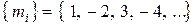Численный метод решения той же задачи с помощью MATLAB приведен ниже.

>> A=Q*Q;

>> SUM=NULL;

>> for k=1:100

SUM=SUM+A^k;

End

>> E=I+SUM;

>> M=E*(I-Q)*inv(I+Q);

Кроме того, дискретное операционное исчисление можно использовать как численный метод решения задач непрерывной математики. Особенностью использования операционного метода для решения дифференциальных уравнений является то, что получить изображение неизвестной функции обычно не очень сложно. Трудности возникают на этапе получения оригинала этого изображения. Во многих случаях оригинал определяется только численно. И здесь может оказаться полезным дискретное операционное исчисление, в котором оператор дифференцирования 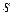приближенно заменяется матричным оператором 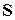. Это возможно в случаях, когда функция, являющаяся решением задачи, незначительно изменяется при увеличении аргумента 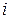на единицу. Можно подобрать период дискретизации решетчатой функции таким образом, чтобы это условие выполнялось. Для порождающей функции 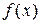, аргументом которых является произведени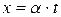е: , где 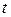– переменная, а 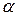– параметр, это условие эквивалентно требованию малости модуля параметра по сравнению с единицей: 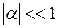. Используя разложение функции 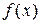в окрестности точки 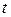в ряд Тейлора, получим:

.

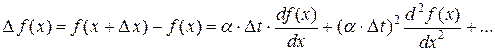Обычно 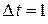. Таким образом, чем меньше по модулю параметр 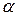, тем меньше приращение функции 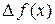. Хотя такой подход не может обеспечить абсолютно точного решения (как и любой другой численный метод), однако результат во многих случаях имеет приемлемую точность. Необходимо только при переходе от непрерывного изображения к матричному его представлению вместо единичной матрицы 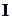использовать матрицу .

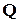Ниже дан пример решения дифференциального уравнения 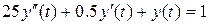при нулевых начальных условиях. Для сравнения приводится точное решение, полученное аналитическим методом.

Y=inv(S*(25*S^2+0.5*S+Q));

OutM=Y*Ve;