Метод ветвей и границ для задачи

Пусть для простоты n = 5. Так как любой план – это некоторый циклический маршрут, то все равно из какого города выходить и в какой город возвращаться. Предположим город № 1. Строим дерево вариантов – вершиной будет город № 1.

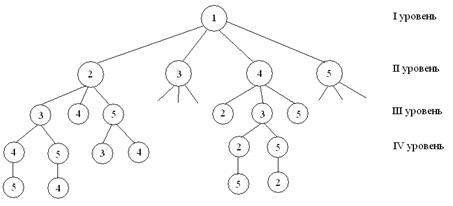
Перебирать планы задачи можно перебирая ветви дерева, начиная с первого узла и заканчивая четвертым уровнем.

Все множество планов можно разбить на четыре подмножества с начальным участком (1, 2), (1, 3), (1, 4), (1, 5).

Подмножество с начальным участком (1, 4) можно разбить на три подмножества (1, 4, 2), (1, 4, 3), (1, 4, 5) и т. д.

Таким образом, при любом n любое подмножество планов задачи на некотором уровне может быть разбито на некоторое количество непересекающихся более мелких подмножеств, исходящих из последнего узла – это есть реальный пример 1.

Предположение 2.

Произвольная задача характеризуется 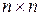матрицей

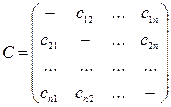
Рассмотрим произвольный план задачи с маршрутом

, , .

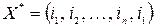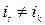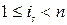Посчитаем минимальные элементы в каждой строке матрицы

.

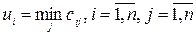Совершим преобразование

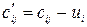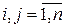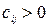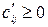, , , (9)

Посчитаем числа

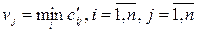
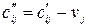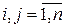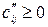, , (10)

Подсчитаем

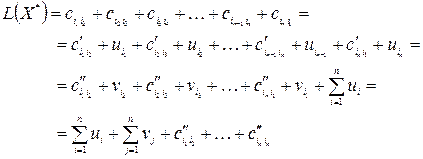
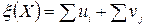
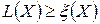
Если же имеется некоторое подмножество планов с начальным участком 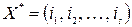, то очевидно, что в качестве 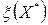можно выбрать

,

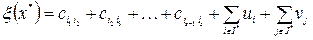где , .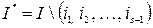

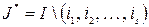3. Метод Гомори для задач целочисленного линейного плана. Построение отсечений. Использование алгоритма.

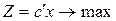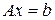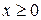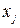, , , – целочисленные, .

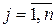Идея метода: вначале отбрасывается условие целочисленности и решается непрерывная задача симплекс-методом.

Строится оптимальный план непрерывной задачи 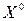. Если все компоненты целочисленные, то это оптимальный план.

Если есть оптимальный план 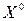и у него имеются дробные компоненты, то по одной из дробных компонент строится дополнительное ограничение, которое называется отсечением.

Отсечение называется правильным, если все планы исходной задачи ему удовлетворяют, а 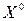не удовлетворяет этому ограничению. Отсечение приводится к равенству, добавляя к основным ограничениям, и новая задача снова решается как непрерывная и т.д.

По этой же схеме строится оптимальный план целочисленной задачи.