 |
Главная Случайная страница Контакты | Мы поможем в написании вашей работы! | |
Додавання взаємно перпендикулярних гармонічних коливань
|
|
Мета роботи – засвоїти метод градуювання звукового генератора за допомогою складання взаємно перпендикулярних коливань.
Прилади та пристрої: електронний осцилограф, звуковий генератор, генератор стандартних сигналів.
Короткі теоретичні відомості
Частоту невідомого гармонічного коливання часто визначають методом фігур Ліссажу. Для цього до досліджуваного коливання додаються взаємно перпендикулярні коливання відомої частоти. У загальному випадку в результаті додавання отримують криві складної форми, що називаються фігурами Ліссажу, за видом яких можна визначити частоту досліджуваної напруги. В цій роботі на пластини вертикального відхилення електронного осцилографа подається досліджувана напруга від джерела коливань звукової частоти, а на пластини горизонтального відхилення – напруга від генератора стандартних сигналів. Завдяки цьому електронний пучок одночасно коливається у двох взаємно перпендикулярних напрямах.
Розглянемо два взаємно перпендикулярних коливання x і y з циклічними частотами 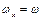 і
і 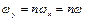 :
:
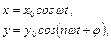
| (33.1) |
де 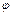 – початкова різниця фаз між коливанням. Очевидно,
– початкова різниця фаз між коливанням. Очевидно,
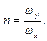
|
Система рівнянь (33.1) у параметричній формі задає траєкторію руху тіла, що одночасно коливається у двох взаємно перпендикулярних напрямах. Визначимо рівняння траєкторії точки, що бере участь у цих коливаннях, в явному вигляді, виключивши час із (33.1). Для цього рівняння перепишемо так:
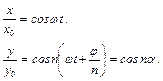
| (33.2) |
Додавши до лівої та правої частин (33.2) уявну частину 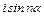 , отримаємо:
, отримаємо:
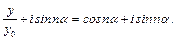
|
За формулою Муавра 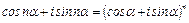 .
.
Тоді 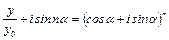 , або
, або
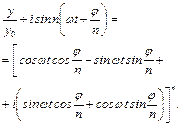
| (33.3) |
Але 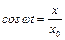 ,
, 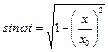 . Тому, підставивши ці значення у формулу (33.3), матимемо:
. Тому, підставивши ці значення у формулу (33.3), матимемо:
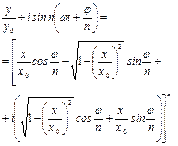
| (33.4) |
Розкладаючи за біномом Ньютона вираз у квадратних дужках і прирівнюючи дійсні частини ліворуч і праворуч, отримуємо рівняння траєкторії коливної точки.
Зупинимося на окремому випадку коливань з однаковими частотами 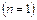 . З формули (33.4) матимемо:
. З формули (33.4) матимемо:
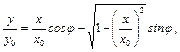
| (33.5) |
звідки

| (33.6) |
Це рівняння сім’ї еліпсів, характеристики яких визначаються різницею фаз  .
.
Розглянемо окремі випадки (рис.33.1, 33.2):
 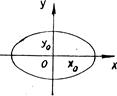 Рис.33.1 Рис.33.2
Рис.33.1 Рис.33.2
|
1. Нехай коливання відбуваються з однаковими фазами, тобто 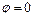 . Тоді рівняння (33.6) набуває вигляду:
. Тоді рівняння (33.6) набуває вигляду:
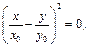 або або 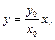
| (33.7) |
тобто еліпс переходить у пряму (див. рис.33.1).
Якщо різниця фаз  , то і в цьому випадку еліпс вироджується в пряму.
, то і в цьому випадку еліпс вироджується в пряму.
2. Якщо різниця фаз між коливаннями дорівнює 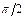 , то рівняння (7) набуває вигляду:
, то рівняння (7) набуває вигляду:
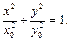
| (33.8) |
Отримали криву – еліпс, осі якого збігаються з осями координат (див. рис.33.2). Якщо амплітуди коливань однакові, еліпс вироджується в коло. Якщо 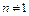 , за загальним видом рівняння, отриманого з формули (33.4), важко зробити висновок про форму траєкторії.
, за загальним видом рівняння, отриманого з формули (33.4), важко зробити висновок про форму траєкторії.
Нехай показник степеня n у рівнянні (33.4) є число раціональне, тобто воно може бути подане у вигляді відношення двох цілих 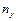 і
і 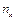 :
:
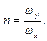
| (33.9) |
Із системи рівнянь (33.1) випливає, що
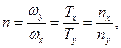
|
де 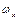 ,
, 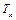 – відповідно циклічна частота і період коливань в напрямі осі x;
– відповідно циклічна частота і період коливань в напрямі осі x; 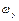 ,
,  – відповідно циклічна частота і період коливань в напрямі осі у.
– відповідно циклічна частота і період коливань в напрямі осі у.
Перепишемо останнє співвідношення у вигляді 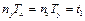 .
.
Отже, за проміжок часу 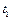 точка здійснює
точка здійснює 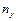 повних коливань в напрямі осі
повних коливань в напрямі осі 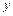 і
і 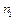 повних коливань в напрямі осі
повних коливань в напрямі осі 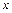 .
.
Після проходження часу 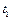 точка буде в тій самій фазі, що і в початковий момент, тобто за наступний проміжок часу
точка буде в тій самій фазі, що і в початковий момент, тобто за наступний проміжок часу 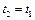 коливання так само повторяться.
коливання так само повторяться.
У результаті коливання будуть накладатись самі на себе і дадуть стійку картину (фігури Ліcсажу). Якщо ж одне з чисел 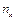 або
або 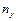 ірраціональне, тобто n не може бути подане у вигляді відношення цілих чисел, то виникає додаткова різниця фаз, завдяки чому траєкторія руху точки неперервно змінюватиметься. Якщо частота одного з коливань відома, то за виглядом фігури Ліссажу визначають частоту іншого. Таке порівняння частот можна здійснити осцилографічним методом, подаючи на пластини горизонтального відхилення напругу з відомою частотою
ірраціональне, тобто n не може бути подане у вигляді відношення цілих чисел, то виникає додаткова різниця фаз, завдяки чому траєкторія руху точки неперервно змінюватиметься. Якщо частота одного з коливань відома, то за виглядом фігури Ліссажу визначають частоту іншого. Таке порівняння частот можна здійснити осцилографічним методом, подаючи на пластини горизонтального відхилення напругу з відомою частотою 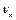 , а на вертикально відхиляючі – досліджувану напругу з частотою
, а на вертикально відхиляючі – досліджувану напругу з частотою 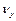 . Враховуючи, що ω=2πν
. Враховуючи, що ω=2πν
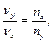
|
тоді
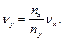
| (33.10) |
Виведемо правило знаходження відношення частот за фігурами Ліссажу. Враховуючи (33.10), перепишемо вираз (33.4) у вигляді
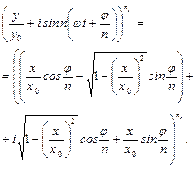
|
Покладемо 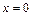 . Тоді, розкладаючи ліву і праву частини за біномом Ньютона та прирівнюючи дійсні частини, отримаємо рівняння
. Тоді, розкладаючи ліву і праву частини за біномом Ньютона та прирівнюючи дійсні частини, отримаємо рівняння 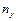 - го степеня відносно у, що має
- го степеня відносно у, що має 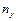 коренів. Графічно це означає, що вісь у перетинає криву
коренів. Графічно це означає, що вісь у перетинає криву 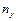 разів. Якщо
разів. Якщо 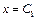 , де
, де 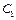 – довільна стала, отримаємо також рівняння, що має
– довільна стала, отримаємо також рівняння, що має 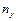 коренів. Фігура Ліссажу буде перетинати будь-яку пряму, паралельну осі y,
коренів. Фігура Ліссажу буде перетинати будь-яку пряму, паралельну осі y, 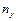 разів. Поклавши
разів. Поклавши  , отримаємо рівняння
, отримаємо рівняння 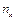 - го степеня відносно x, тобто крива перетинатиме пряму, паралельну осі x,
- го степеня відносно x, тобто крива перетинатиме пряму, паралельну осі x, 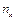 разів. Звідси випливає таке правило знаходження частот. Проводять через дану фігуру дві довільні взаємно перпендикулярні прямі AB і CD, паралельні осям х і y (рис.33.3). Підраховують число точок перетину кривої з прямими CD (
разів. Звідси випливає таке правило знаходження частот. Проводять через дану фігуру дві довільні взаємно перпендикулярні прямі AB і CD, паралельні осям х і y (рис.33.3). Підраховують число точок перетину кривої з прямими CD (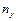 ) і AВ (
) і AВ (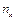 ). У випадку
). У випадку 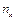 = 3 і
= 3 і 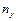 = 1 (рис.33.3), тобто
= 1 (рис.33.3), тобто
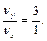
|
Якщо пряма проходить через точку перетину віток кривої, при відліку її рахують двічі (така точка відповідає кратним кореням).
Дата публикования: 2014-11-04; Прочитано: 2717 | Нарушение авторского права страницы | Мы поможем в написании вашей работы!
