Дифференциальные уравнения равновесия жидкости (Уравнения Л. Эйлера)

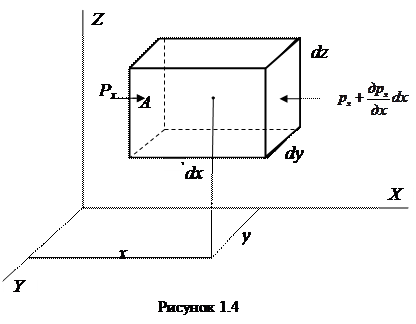
В жидкости, находящейся в состоянии покоя, выделим бесконечно малый прямоугольный параллелепипед с ребрами dx, dy и dz (рисунок 1.4), параллельными осям прямоугольных координат. Давление жидкости на грани параллелепипеда объемом dxdydz выразим соответствующими величинами гидростатических давлений. На грань dzdy будет действовать среднее гидростатическое давление р_х. На грань, противоположную ей, будет действовать гидростатическое давление

,

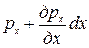где др_х/дх - частная производная от р_х по Х, характеризующая изменение давления на единицу длины в направлении оси Х, т.е. выражение 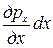показывает приращение среднего давления р_х на длине dx.

На другие грани соответственно будут действовать средние гидростатические давления:

р_y и 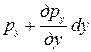; р_z и .

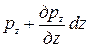Помимо сил гидростатического давления на каждую единицу объема параллелепипеда действуют массовые силы. Равнодействующую этих сил выразим через G, а ее проекции, отнесенные к единице массы, на соответствующие оси координат обозначим через X, Y и Z. Сумму проекций всех сил на соответствующие координатные оси можно представить в виде:

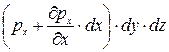– + r×dx×dy×dz×X =0;

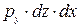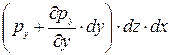– + r×dx×dy×dz×Y= 0; (1.9)

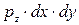– + r×dx×dy×dz×Z =0,

где ρ - плотность жидкости.

Преобразуя уравнения (1.9), получаем:

– + r×X= 0;

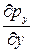– + r×Y =0; (1.10)

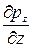– + r×Z =0.

Перепишем уравнения (1.10), разделив их на ρ:

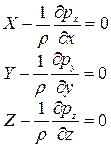. (1.11)

Уравнения (1.11) являются уравнениями равновесия жидкости в общем виде, описывающими закон распределения гидростатического давления и называются уравнениями гидростатики Л. Эйлера.

Умножая в системе уравнений (1.11) первое уравнение на dx, а последующие – на dy и dz и складывая их, получим

. (1.12)

Выражение в скобках левой части уравнения (1.12) представляет собой полный дифференциал. Поэтому это уравнение можно записать в виде:

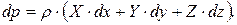(1.13)

Это уравнение называется дифференциальным уравнением равновесия жидкостей или характеристическим уравнением.