Гидростатическое давление и его свойства

Выделим в покоящейся жидкости некоторый ее объем V (рисунок 1.1), который находится в равновесии под действием сил Р₁, Р₂, Р₃, Р₄, Р₅, Р₆.

Плоскостью АВ разделим его на две части I и II.

Мысленно уберем I часть в сторону. В результате этого II часть, оказавшись неуравновешенной, начнет под действием сил Р₄, Р₅, Р₆ двигаться вверх.

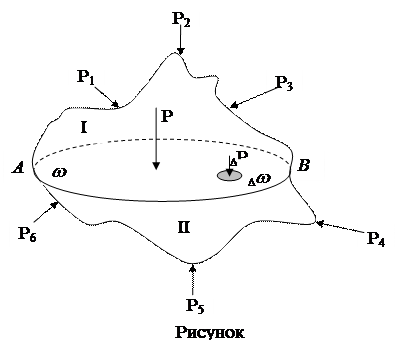Для предотвращения этого приложим к площади w силу Р. На долю элементарной площадки _D w от общей уравновешивающей силы Р придется элементарная сила _DР.

Разделив силу _DР на площадь _D w получим среднее гидростатическое давление, [Н/м²]:

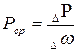. (1.2)

Уменьшая размеры площадки _D w и переходя к пределу при стремлении к нулю величины _D w, получим величину гидростатического давления в точке жидкости

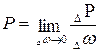. (1.3)

Гидростатическим давлением называется напряжение, возникающее в жидкости в результате действия сжимающих сил.

Гидростатическое давление обладает следующими свойствами:

1. 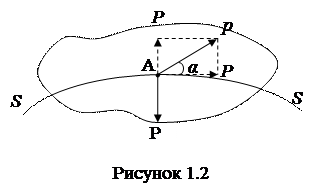Гидростатическое давление всегда направлено по нормали к поверхности. Это свойство доказывается от противного. Проведем в покоящейся жидкости (рисунок 1.2) произвольную поверхность S-S. Пусть в точке А, лежащей на этой поверхности, гидростатическое давление р направлено не по нормали, а под углом α. Тогда давление р можно разложить на касательное р_к и нормальное р_н. Так как жидкость находится в равновесии, то касательное напряжение отсутствует (р_к =0), т.е. действует только давление р_н. Известно, что жидкость не воспринимает растягивающих усилий и при направлении р_н по внешней нормали она приходила бы в движение, а это противоречит условию равновесия. Следовательно давление Р направлено по нормали внутрь жидкости.

2. Гидростатическое давление в данной точке по всем направлениям одинаково. Для доказательства этого свойства гидростатического давления в покоящейся жидкости выберем прямоугольную систему координат. В пределах координатных осей около точки А построим элементарный тетраэдр, ребра которого dx, dy, dx параллельны осям координат (рисунок 1.3).

Предположим, что жидкость в объеме этого тетраэдра затвердела; поэтому можно рассматривать тетраэдр как твердое тело. На тетраэдр действуют внешние силы: по граням

; ; :

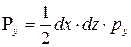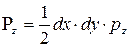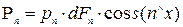, (1.4)

Рисунок 1.3

и массовая сила, приложенная в центре тяжести тетраэдра:

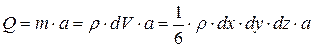, (1.5)

где а - равнодействующее ускорение всех массовых сил.

Так как тетраэдр находится в равновесии, то все действующие на него силы взаимно уравновешены, а потому суммы проекций всех этих сил на координатные оси должны равняться нулю. Рассмотрим сначала проекции на одну из осей, например на ось х:

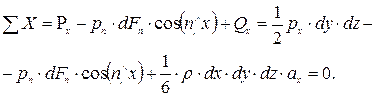(1.6)

Учитывая, что в направлении оси Х проекция площади , перепишем равенство (1.6), сократив его на :

. (1.7)

. (1.8)

При бесконечном уменьшении ребер тетраэдра он превращается в точку, при этом dx=dy=dz= 0 и ранее полученное равенство дает Р_х=Р_п.

Аналогичные рассуждения можно привести относительно проекций сил на оси Y и Z, поэтому можно написать: Р_х=Р_п; Р_y=Р_п; Р_z=Р_п; или

Р_х=Р_y=Р_z=Р.