 |
Главная Случайная страница Контакты | Мы поможем в написании вашей работы! | |
Окружность. Мы изучили линейные уравнения, задающие прямые
|
|
Мы изучили линейные уравнения, задающие прямые. Теперь мы рассмотрим уравнение второй степени с двумя переменными:
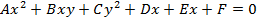 ,
,
где, по крайней мере один из коэффициентов 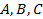 не равен нулю (в противном случае уравнение превращается в линейное). Изучим вопрос о том, какие линии определяются этим уравнением. Для начала рассмотрим некоторые частные случаи.
не равен нулю (в противном случае уравнение превращается в линейное). Изучим вопрос о том, какие линии определяются этим уравнением. Для начала рассмотрим некоторые частные случаи.
Ранее мы видели, что окружность с центром в точке 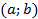 и радиусом
и радиусом 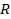 имеет уравнение
имеет уравнение
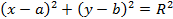 . (4.23)
. (4.23)
Раскрывая скобки, получим 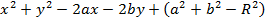 или
или
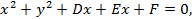 (4.24)
(4.24)
где
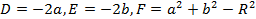 .
.
Уравнение (4.24) является уравнением второй степени. Итак, окружность задается (имеет) уравнением второй степени относительно текущих координат. Подчеркнем, что в уравнении (4.24) коэффициенты при квадратах координат равны, а член с произведением координат отсутствует. Очевидно и обратное: при выполнении этих двух условий уравнение, вообще говоря, определяет окружность, так как приводится к виду (4.24) путем деления на коэффициент при 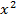 .
.
Итак, по виду данного уравнения второй степени мы можем решить, является ли оно уравнением окружности или нет. Например, уравнение
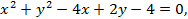 (4.25)
(4.25)
определяет окружность, так как в нем коэффициенты при квадратах координат равны между собой, а член с произведением координат отсутствует. Желая построить эту окружность, мы должны определить координаты ее центра и радиус. С этой целью рассмотрим в нем члены, содержащие 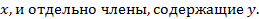 Выделяя в них полные квадраты, получим:
Выделяя в них полные квадраты, получим: 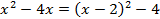 ,
, 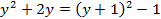 . Тогда, уравнение (4.25) примет вид:
. Тогда, уравнение (4.25) примет вид:  +
+ 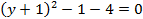 или
или 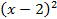 +
+ 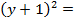 9. Сравнивая последнее уравнение с (4.23), видим, что
9. Сравнивая последнее уравнение с (4.23), видим, что 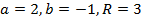 . Таким образом, центром окружности является точка (2;-1) и ее радиус равен 3.
. Таким образом, центром окружности является точка (2;-1) и ее радиус равен 3.
Эллипс
Эллипсом называется геометрическое место точек, сумма расстояний от каждой из которых до двух заданных точек, называемых фокусами, постоянна.
Очевидно, что эта сумма не может быть меньше расстояния между фокусами, если же она равна этому расстоянию, то рассматриваемым геометрическим местом точек будет отрезок прямой между фокусами.
Чтобы найти уравнение эллипса, проведем ось абсцисс через фокусы 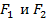 , выбрав на ней положительное направление от
, выбрав на ней положительное направление от  к
к 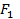 ; начало координат возьмем в середине отрезка
; начало координат возьмем в середине отрезка 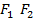 , (рис.4.10). Обозначим через
, (рис.4.10). Обозначим через 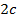 расстояние между фокусами. Координаты фокусов
расстояние между фокусами. Координаты фокусов 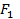 и
и  будут соответственно
будут соответственно 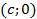 и
и 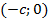 . Пусть
. Пусть 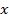 и
и 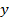 координаты произвольной точки
координаты произвольной точки 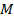 эллипса, тогда
эллипса, тогда
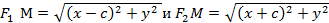 .
.
По определению эллипса сумма 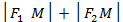 есть величина постоянная. Обозначим ее через
есть величина постоянная. Обозначим ее через 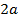 , тогда
, тогда
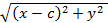 +
+ 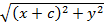 = 2a.
= 2a.
Это и есть уравнение эллипса в выбранной системе координат.
Упростим его, для этого освободимся от радикалов, имеем:
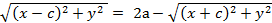 .
.
Возводя обе части этого равенства в квадрат, получим:
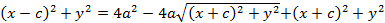 ,
,
или, раскрывая скобки и приводя подобные
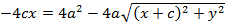 , т.е.
, т.е. 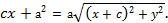
Снова возведем в квадрат обе части последнего равенства:
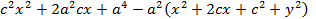 или
или 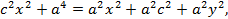
т.е. 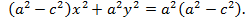 Разделив обе части на
Разделив обе части на 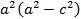 , получим:
, получим:
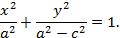
Так как по условию 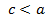 , то
, то 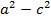 есть положительная величина, ее принято обозначать через
есть положительная величина, ее принято обозначать через 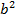 .
.
| x |

|
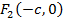
|
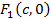
|
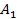
|
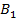
|
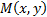
|
| y |
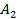
|

|
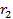
|
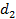
|
| x |
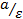
|
| y |
| M |
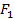
|

|
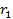
|
| Рис.4.10. Эллипс. |
| Рис.4.11. Директрисы эллипса |
Тогда уравнение эллипса примет вид:
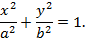
где
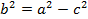
Уравнение (4.26) называется каноническим уравнением эллипса. Очевидно, что ему удовлетворяют координаты любой точки эллипса и, как можно показать, никакие другие.
Так как уравнение (4.26) содержит только квадраты текущих координат, то оси координат являются осями симметрии эллипса. Ось симметрии, на которой находятся фокусы, называется фокальной. Точка пересечения осей симметрии называется центром эллипса. Для эллипса, заданного уравнением (4.26), фокальная ось совпадает с осью абсцисс, а центром является начало координат.
Точки пересечения эллипса с осями симметрии называются его вершинами. Эллипс, заданный уравнением (4.26), имеет вершинами точки (рис.4.10): 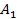 (
(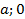 ),
), 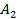 (
(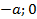 ),
), 
Отрезки 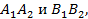 соединяющие противоположные вершины эллипса, называются соответственно большой и малой осями эллипса, их длины
соединяющие противоположные вершины эллипса, называются соответственно большой и малой осями эллипса, их длины 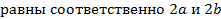 . Длины
. Длины 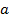 и
и 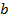 называются соответственно большой и малой полуосями эллипса. При
называются соответственно большой и малой полуосями эллипса. При 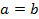 уравнение (4.26) принимает вид
уравнение (4.26) принимает вид 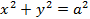 и определяет окружность.
и определяет окружность.
Обозначим через 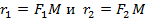 расстояние от произвольной точки
расстояние от произвольной точки 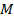 эллипса до соответствующих фокусов. Тогда
эллипса до соответствующих фокусов. Тогда
 (4.28)
(4.28)
С другой стороны, 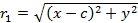 и
и 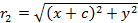 , где
, где 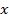 , y - координаты точки
, y - координаты точки 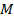 эллипса. Возводя эти равенства в квадрат, и вычитая из второго первое, получаем:
эллипса. Возводя эти равенства в квадрат, и вычитая из второго первое, получаем:
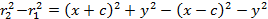 .
.
Раскрывая скобки и приводя подобные, находим:
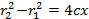 (4.29)
(4.29)
Уравнение (4.29) перепишем в виде 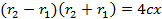 . Учитывая равенство (4.28), имеем:
. Учитывая равенство (4.28), имеем: 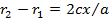 . Решая полученное уравнение совместно с уравнением (4.28), найдем, что
. Решая полученное уравнение совместно с уравнением (4.28), найдем, что
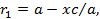
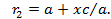
Величина 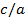 , входящая в последние формулы, называется эксцентриситетом эллипса; мы будем обозначать ее через
, входящая в последние формулы, называется эксцентриситетом эллипса; мы будем обозначать ее через 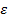 . Эксцентриситет есть отношение фокусного расстояния к длине большой оси, причем
. Эксцентриситет есть отношение фокусного расстояния к длине большой оси, причем 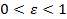 . так как
. так как 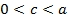 (для окружности
(для окружности 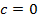 и
и 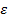 =0). С учетом принятого обозначения, мы получили следующие формулы для фокальных радиусов
=0). С учетом принятого обозначения, мы получили следующие формулы для фокальных радиусов 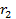 и
и 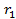 :
:
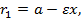
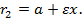
Рассмотрим прямую 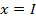 (
(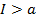 ), параллельную оси ординат, и найдем расстояние
), параллельную оси ординат, и найдем расстояние 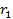 от произвольной точки
от произвольной точки 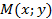 эллипса до его правого фокуса и расстояние
эллипса до его правого фокуса и расстояние  от этой точки
от этой точки 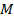 до прямой
до прямой 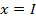 (рис.4.11). Вычислим отношение этих расстояний.
(рис.4.11). Вычислим отношение этих расстояний.
Так как 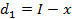 , то
, то
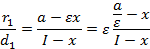
Если 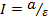 , то отношение
, то отношение 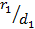 будет сохранять постоянное значение, равное
будет сохранять постоянное значение, равное 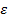 . В силу симметрии то же можно сказать относительно левого фокуса и прямой с уравнением
. В силу симметрии то же можно сказать относительно левого фокуса и прямой с уравнением 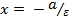 .
.
Две прямые, перпендикулярные к фокальной оси эллипса и отстоящие на расстоянии 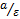 от его центра, называются директрисами эллипса, они обладают следующим свойством: отношение расстояний от любой точки эллипса до фокуса и соответствующей директрисы есть величина постоянная, равная эксцентриситету.
от его центра, называются директрисами эллипса, они обладают следующим свойством: отношение расстояний от любой точки эллипса до фокуса и соответствующей директрисы есть величина постоянная, равная эксцентриситету.
Пример 4.19. Найти эксцентриситет и директрисы эллипса 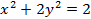 .
.
Написав уравнение эллипса в виде  заключаем, что
заключаем, что 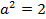 ,
, 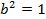 . Следовательно,
. Следовательно, 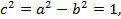 откуда
откуда

Уравнения директрис: 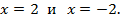
Пусть эллипс задан своим каноническим уравнением 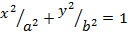
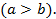 Рассмотрим уравнение окружности
Рассмотрим уравнение окружности 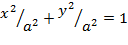 , описанной около эллипса (рис. 4.12).
, описанной около эллипса (рис. 4.12).
Назовем две точки 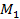 и
и 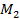 , лежащие соответственно на эллипсе и окружности, соответствующими точками, если они имеют одинаковую абсциссу
, лежащие соответственно на эллипсе и окружности, соответствующими точками, если они имеют одинаковую абсциссу 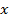 и лежат по одну и ту же сторону от оси
и лежат по одну и ту же сторону от оси 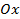 . Обозначим их ординаты соответственно через
. Обозначим их ординаты соответственно через 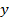 и
и 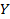 , тогда
, тогда 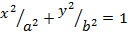 ,
, 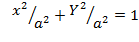 . Сравнив последние уравнения, заключаем, что
. Сравнив последние уравнения, заключаем, что 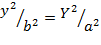 . Разрешая это уравнение относительно
. Разрешая это уравнение относительно 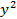 , получаем:
, получаем: 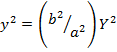 , откуда окончательно
, откуда окончательно 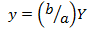 .
.
Так как 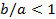 , то положим
, то положим  , тогда
, тогда 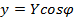 . Эта формула показывает, что величина
. Эта формула показывает, что величина 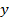 вектора
вектора 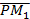 может рассматриваться как проекция вектора
может рассматриваться как проекция вектора  (рис.4.13), если угол между
(рис.4.13), если угол между 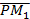 и
и  принять равным
принять равным 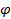 .
.
| x |
| y |
| 0 |
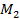
|
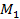
|
| p |
| Рис. 4.12. Соответствующие точки. |
| Рис. 4.13. Эллипс, как проекция окружности |
Отсюда следует, что если поместить окружность в плоскости, наклоненной к плоскости эллипса под углом 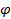 , то эллипс будет являться ортогональной проекцией этой окружности.
, то эллипс будет являться ортогональной проекцией этой окружности.
Координаты соответствующих точек 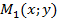 и
и 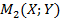 эллипса и окружности связаны соотношениями:
эллипса и окружности связаны соотношениями:
 ,
,
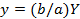 , (4.30)
, (4.30)
а параметрические уравнения окружности имеют вид:
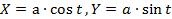 , (4.31)
, (4.31)
Заменяя в (4.30) 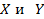 их выражениями из (4.31), получим
их выражениями из (4.31), получим
 и
и 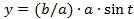 ,
,
или окончательно
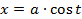 ,
,
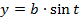 .
.
Это и есть параметрические уравнения эллипса.
Заключая этот параграф, рассмотрим эллипс, центр которого находится в точке с координатами 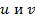 . Такой эллипс задается уравнением
. Такой эллипс задается уравнением
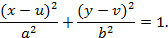
Дата публикования: 2014-11-02; Прочитано: 431 | Нарушение авторского права страницы | Мы поможем в написании вашей работы!
