Ошибки выборки. При любом статистическом наблюдении (сплошном и выборочном) могут встретиться ошибки двух видов: регистрации и репрезентативности

При любом статистическом наблюдении (сплошном и выборочном) могут встретиться ошибки двух видов: регистрации и репрезентативности. Ошибки регистрации могут иметь случайный и систематический характер. Случайные ошибки складываются из множества различных неконтролируемых причин, носят непреднамеренный характер и обычно по совокупности уравновешивают друг друга (например, изменения показателей прибора при температурных колебаниях в помещении).

Систематические ошибки тенденциозны, так как нарушают правила отбора объектов в выборку (например, отклонения в измерениях при изменении настройки измерительного прибора).

Пример. Для оценки социального положения населения в городе предусмотрено обследовать 25% семей. Если при этом выбор каж­дой четвертой квартиры основан на ее номере, то существует опас­ность отобрать все квартиры только одного типа (например, одно­комнатные), что обеспечит систематическую ошибку и исказит ре­зультаты; выбор же номера квартиры по жребию более предпочтите­лен, так как ошибка будет случайной.

Ошибки репрезентативности присущи только выборочному наблюдению, их невозможно избежать. Они возникают в результате того, что выборочная совокупность не полностью воспроизводит ге­неральную. Значения показателей, получаемых по выборке, отлича­ются от показателей этих же величин в генеральной совокупности (или получаемых при сплошном наблюдении).

Ошибка выборочного наблюдения 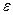есть разность между значе­нием параметра в генеральной совокупности и ее выборочным зна­чением. Для среднего значения количественного признака она равна: 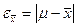, а для доли (альтернативного признака) .

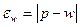Ошибки выборки свойственны только выборочным наблюдениям. Чем больше эти ошибки, тем больше эмпирическое распределение отличается от теоретического распределения. Параметры эмпирического распре­деления 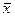и 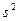являются случайными величинами, следовательно, ошибки выборки также являются случайными величинами и могут принимать для разных выборок разные значения. Поэтому принято исчислять среднюю ошибку.

Средняя ошибка выборки есть величина 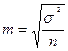, выражающая среднее квадратическое отклонение выборочной средней от математического ожидания. Эта величина при соблюдении принципа случайного отбора зависит, прежде всего, от объема выборки n и степени варьирования признака: чем больше п и чем меньше вариация признака (следовательно, и значение 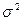), тем меньше величина средней ошибки выборки т. Соотношение между дисперсиями генеральной и выборочной совокупностей выражается формулой

,

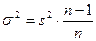т. е. при достаточно больших п можно считать, что 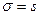. Средняя ошибка выборки показывает возможные отклонения параметра выборочной совокупности от параметра генеральной. В табл. 9.2 приведены выражения для вычисления средней ошибки т выборки при разных методах организации наблюдения.

Таблица 9.2

Средняя ошибка 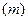выборочной средней 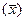и доли 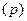для разных видов выборки

Вид выборки	Отбор
повторный	бесповторный
Количественный признак
Собственно-случайная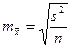
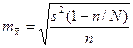
Механическая	-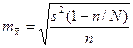
Типическая (стратифициро­ванная)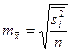
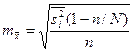
Серийная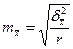
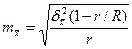
Альтернативный признак
Собственно-случайная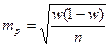
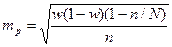
Механическая	-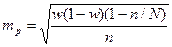
Типическая (стратифициро­ванная)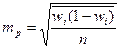
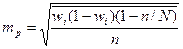
Серийная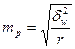

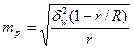
В табл. 9.2 приняты следующие условные обозначения:

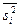- средняя величина из внутригрупповых выборочных дисперсий для непрерывного признака;

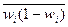- средняя величина из внутригрупповых дисперсий доли;

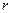- число отобранных серий;

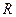- общее число серий.

,

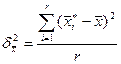где 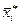- средняя величина 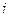- ой серии;

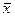- общая средняя по всей выборочной совокупности для непрерывного признака.

,

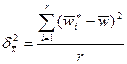где 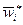- доля признака в i - й серии;

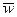- общая доля признака по всей выборочной совокупности.

Однако о величине средней ошибки т можно судить лишь с определенной вероятностью P (Р < 1). A. M. Ляпунов доказал, что распределение выборочных средних 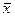, а следовательно, и их откло­нений от генеральной средней, при достаточно большом числе n приближенно подчиняется нормальному закону распределения при условии, что генеральная совокупность обладает конечной средней и ограниченной дисперсией.

Математически это утверждение для средней величины выражается в виде

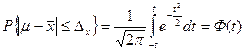, (1)

а для доли выражение (1) примет вид

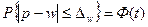, (2)

где 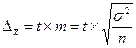- есть предельная ошибка выборки, которая кратна величине средней ошибки выборки т, а коэффициент кратности t ("коэффициент доверия") берется согласно критерию Стьюдента, предложенного У. С. Госсетом (псевдоним "Student"); значения t для разного объема выборки п берутся из таблицы, которая приведена в приложении 2.

Значения функции 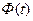при некоторых значениях t равны:

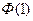= 0,683; Ф (1,5) = 0,866; Ф (2) = 0,954; Ф (2,5) = 0,988; Ф (3) = 0,997; Ф (3,5) = 0,999. (3)

Следовательно, выражения (3) могут быть прочитаны так: с ве­роятностью Р = 0,683 (68,3%) можно утверждать, что разность между выборочной и генеральной средней не превысит одной величины средней ошибки m { t = 1), с вероятностью Р = 0,954 (95,4%) - что она не превысит величины двух средних ошибок m { t = 2), с вероятностью Р = 0,997 (99,7%) - не превысит трех значений т (t = 3). Таким обра­зом, вероятность того, что эта разность превысит трехкратную вели­чину средней ошибки, определяет уровень ошибки и составляет не более 0,3%.

В табл. 9.3 приведены формулы для вычисления предельной ошибки выборки.

Таблица 9.3

Предельная ошибка 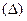выборки для средней 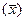и доли 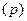для