 |
Главная Случайная страница Контакты | Мы поможем в написании вашей работы! | |
Решение задач линейного программирования симплекс-методом
|
|
Идея разработана русским ученым Канторовичем Л.В. в 1939 году. На основе этой идеи американский ученый Д. Данциг в 1949 году разработал симплекс-метод, позволяющий решить любую задачу линейного программирования.
Основные теоремы линейного программирования:
1. Если задача линейного программирования имеет оптимальное решение, то оно совпадает, по крайней мере, с одним из опорных решений системы ограничительных уравнений. Другими словами если задача линейного программирования имеет оптимальное решение, то оно совпадает, хотя бы с одной из вершин области системы ограничений.
2. Об альтернативном оптимуме. Если максимум или минимум линейной функции достигается в нескольких опорных решениях, то любое оптимальное решение есть выпуклая линейная комбинация оптимальных решений.
Геометрически интерпретация данной теоремы означает, что в случае альтернативного оптимума линии уровня проходят через две вершины области допустимых решений, в этом случае оптимальным решением становиться любая точка отрезка, соединяющего эти вершины.
Геометрическая интерпретация симплекс-метода:
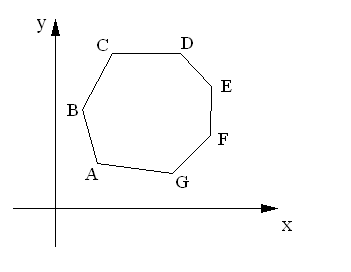
Из приведенных выше основных теорем линейного программирования следует, что если задача линейного программирования имеет оптимальное решение, то оно соответствует хотя бы одной угловой точке многогранника решений и совпадает, по крайней мере, с одним из допустимых базисных решений системы ограничений.
На основании этого можно предложить достаточно простой метод решения задачи линейного программирования, который сводится к следующей принципиальной схеме:
· необходимо найти все опорные решения (точки многогранника), множество которых является конечным;
· Вычислить для каждого из опорных решений значение целевой функции;
· Сравнить значения целевой функции в каждом из опорных решений и выбрать оптимальное (максимальное или минимальное).
Теоретически данная схема приведет к нахождению оптимального решения, но практически ее существование связано с большими вычислительными трудностями. Даже в задаче с двумя переменными число опорных решений может оказаться очень большим, а при большом значении переменных оно может достигать огромных чисел и практически осуществление данного перебора станет невозможным. Эти вычислительные трудности возникают в результате того, что рассмотренная принципиальная схема связана с простым перебором опорных решений, т.н. в этой схеме не принимается во внимание тот факт, насколько новое испытуемое решение улучшает значение целевой функции и приближает нас к оптимальному решению.
Если же перебор опорных решений производить направленно, т.е. на каждом шаге улучшая (или, по крайней мере, не ухудшая) значение целевой функции, то число перебираемых опорных решений можно резко сократить. При использовании такой схемы в отличие от первой, каждое последующее опорное решение выбирается таким образом, чтобы оно было лучше, (или, по крайней мере, не хуже) предыдущего, именно поэтому на каждом из шагов значение целевой функции улучшается (или, по крайней мере, не ухудшается)
Необходим метод направленного перебора точек, для практического применения метода направленного перебора необходимо знать:
1. Алгоритм определения какого-либо первоначального, допустимого решения.
2. Алгоритм перехода к лучшему или к не худшему решению.
3. Признак, указывающий на то, что найденное решение оптимально.
Симплекс-метод является методом направленного перебора.
Геометрически интерпретация симплекс метода состоит в последовательном переходе от одной вершины многогранника к другой (от первоначально выбранной вершины к одной из соседних вершин, а именно к той, у которой линейная функция принимает лучшее, или по крайней мере, не худшее значение). Этот процесс происходит до тех пор пока не будет найдено оптимальное решение – вершина, где достигается оптимальное решение функции (если задача имеет конечный оптимум).
Задачу симплекс-методом можно решить и аналитически, рассмотрим алгоритм решения.
Алгоритм симплекс-метода:
1. Выделяем исходный допустимый базис и заполняем первую симплекс-таблицу.
2. Если в последней строке, полученной таблицы кроме, быть может, первого числа нет положительных чисел, то базисное решение является оптимальным, задача решена.
3. Пусть среди указанных в п.2. чисел имеется положительное число, например в столбе xj, отмечаем этот столбец вертикальной стрелкой, просматриваем остальные числа столбца, если среди них нет положительных чисел, то минимум рассматриваемой функции равен бесконечности и задача решения не имеет.
4. Пусть среди просмотренных в п.3. чисел имеются положительные числа, для каждого из таких чисел a составляем отношение 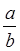 , где b – первое число в той же строке, т.е. свободный член. Из всех таких отношений выбираем наименьшее. Пусть оно соответствует строке для базисного переменного xi, отмечаем эту строку горизонтальной стрелкой. Число
, где b – первое число в той же строке, т.е. свободный член. Из всех таких отношений выбираем наименьшее. Пусть оно соответствует строке для базисного переменного xi, отмечаем эту строку горизонтальной стрелкой. Число 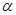 , стоящее в отмеченной строке и столбце и называется разрешающим элементом таблицы.
, стоящее в отмеченной строке и столбце и называется разрешающим элементом таблицы.
5. Переходим к новой таблице, для этого отмеченную строку умножаем на 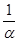 , чтобы на месте разрешающего элемента появилась 1, и пишем ее на месте прежней. В каждой из остальных строк таблицы прибавляем строку, полученную на месте полученной строки, умноженную на такое число, чтобы элемент, стоящий в отмеченном столбце обратился в 0. Полученную строку пишем на месте прежней.
, чтобы на месте разрешающего элемента появилась 1, и пишем ее на месте прежней. В каждой из остальных строк таблицы прибавляем строку, полученную на месте полученной строки, умноженную на такое число, чтобы элемент, стоящий в отмеченном столбце обратился в 0. Полученную строку пишем на месте прежней.
6. С новой таблицей возвращаемся к выполнению пункта 2.
1. Рассмотрим пример решения задачи линейного программирования симплекс-методом.
f(x) = x4 – x5 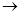 min
min
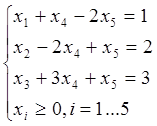
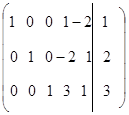
Если в целевой функции нет базисных переменных, то выражаем ее
f(x) = x4 – x5 = 0
Строим первую симплекс-таблицу
| Базовые переменные | Свободный член | х1 | х2 | х3 | х4 | х5 |
| х1 | -2 | |||||
| х2 | -2 | |||||
| х3 | ||||||
| f(x) | -1 |
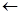
Строим вторую симплекс-таблицу
| Базовые переменные | Свободный член | х1 | х2 | х3 | х4 | х5 | |
| х1 | -3 | ||||||
| х5 | -2 | ||||||
| х3 | 0,2 | -0,2 | 0,2 | 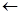
| |||
| f(x) | -2 | -1 |
Третья симплекс-таблица
| Базовые переменные | Свободный член | х1 | х2 | х3 | х4 | х5 |
| х1 | 5,6 | 1,4 | 0,6 | |||
| х5 | 2,4 | 0,6 | 0,4 | |||
| х4 | 0,2 | -0,2 | 0,2 | |||
| f(x) | -2,2 | -0,8 | -0,2 |
Ответ:
f(x)min = -2,2, при
х1 = 5,6
х2 = 0
х3 = 0
х4 = 0,2
х5 = 2,4
2. Если в целевой функции имеются базисные неизвестные, возникает вопрос, как наиболее рационально находить выражения целевой функции через свободные неизвестные.
Пусть целевая функция первоначально имеет следующий вид
f(x) = c0 + c1x1 + c2x2 + … + cnxn 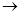 min
min
Пусть мы выделили допустимый базис и заполнили симплекс-таблицу, кроме последней строки, допустим базис – х1, х2, х3, остальные – свободные члены.
| с0 | с1 | с2 | … | cn | ||
| Базовые переменные | Сводные члены | x1 | x2 | … | xn | |
| c1 | x1 | |||||
| c2 | x2 | |||||
| c3 | x3 | |||||
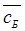
| f(x) | 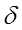
| 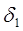
| 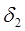
| … | 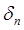
|
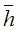
| 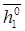
| 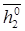
| … | 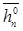
| ||
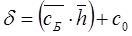
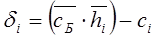
Рассмотрим пример
f(x) = 2x1 – x2 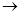 min
min
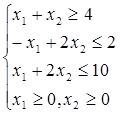
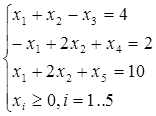
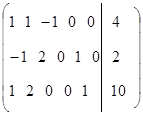 ~
~ 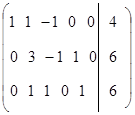
| -1 | |||||||
| Базовые переменные | Сводные члены | x1 | x2 | x3 | x4 | x5 | |
| x1 | -1 | ||||||
| x4 | 6/2 | 0/0 | 3/1 | -1/ 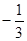
| 1/ 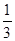
| 0/0 | |
| x5 | |||||||
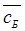
| f(x) | -2 | |||||
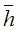
| 
|
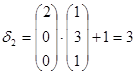
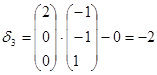
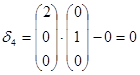
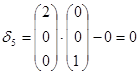
| -1 | |||||||
| Базовые переменные | Сводные члены | x1 | x2 | x3 | x4 | x5 | |
| x1 | -2/3 | -1/3 | |||||
| -1 | x2 | -1/3 | 1/3 | ||||
| x5 | 4/3 | -1/3 | |||||
| f(x) | -1 | -1 |
Ответ:
f(x)min =2
x1 = 2
x2 = 2
x3 = 0
x4 = 0
x5 = 4
3. При решении задач линейного программирования симплекс-методом критерием оптимальности является условие
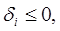 где
где 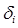 - коэффициенты при неизвестных
- коэффициенты при неизвестных
Если на каком-либо шаге окажется, что хотя бы одна оценка свободной переменной равна 0, а остальные 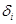 < 0, то это является признаком того, что задача имеет альтернативный оптимум.
< 0, то это является признаком того, что задача имеет альтернативный оптимум.
Мы принимаем в качестве ключевого столбца, где 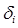 = 0 и ищем новое оптимальное решение. При этом значение целевой функции не измениться.
= 0 и ищем новое оптимальное решение. При этом значение целевой функции не измениться.
В этом случае если только одна оценка свободной переменной равна 0, то
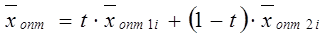 , где
, где 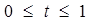
Если две оценки и более, например s свободных элементов равно 0, то оптимальное решение определяется по формуле
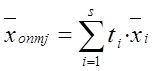 , где
, где 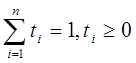
Пример:
f(x) = 2x2 – 4x3 + 2x5  min
min
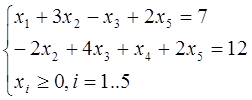
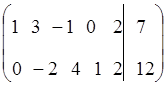
| -4 | ||||||||
| Базисныеые переменные | Сводные члены | x1 | x2 | x3 | x4 | x5 | ||
| x1 | -1 | |||||||
| x4 | 12/3 | 0/0 | -2/-0.5 | 4/1 | 1/0.25 | 2/0.5 | 
| |
| f(x) | -2 | -2 | ||||||
| ||||||||
| -4 | ||||||||
| Базовые переменные | Сводные члены | x1 | x2 | x3 | x4 | x5 | ||
| x1 | 10/4 | 1/0.4 | 2.5/1 | 0.25/0.1 | 2.5/1 | 
| ||
| -4 | x3 | -0.5 | 0.25 | 0.5 | ||||
| f(x) | -12 | -1 | -4 | |||||
|
f(x)min = -12, при
х1 = 10
х2 = 0
х3 = 3
х4 = 0
х5 = 0
| -4 | ||||||||
| Базовые переменные | Сводные члены | x1 | x2 | x3 | x4 | x5 | ||
| x2 | 0.4 | 0.1 | ||||||
| -4 | x3 | 0.2 | 0.3 | |||||
| f(x) | -12 | -1 | -4 | |||||
f(x)min = -12, при
х1 = 0
х2 = 4
х3 = 5
х4 = 0
х5 = 0
х1 = 10 * t + (1 – t) * 0 = 10
х2 = 0 * t + (1 – t) * 4 = 4 – 4t
х3 = 3 * t + (1 – t) * 5 = 5 – 2t
х4 = 0
х5 = 0
f(x)min = -12, при
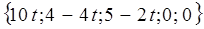 ,
, 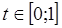
Дата публикования: 2014-11-04; Прочитано: 1567 | Нарушение авторского права страницы | Мы поможем в написании вашей работы!
