Симметрические преобразования

Определение. Линейное преобразование A евклидова пространства E_n называется симметрическим (или самосопряженным)преобразованием, если для любых векторов a и b имеет место равенство

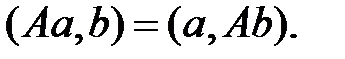(7.7)

Примером симметрического преобразования является линейное преобразование, при котором всякий вектор умножается на фиксированное число

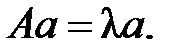
Теорема7.3. Симметрическое преобразование Aевклидова пространства в любом ортонормированном базисе задается симметричной матрицей. Обратно, если линейное преобразование пространства хотя бы в одном ортонормированном базисе задается симметричной матрицей, то это преобразование симметрическое.

Доказательство. Пусть симметрическое преобразование евклидова пространства в ортонормированном базисе e ₁, e ₂,…, e_n задается матрицей 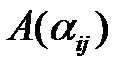. Тогда

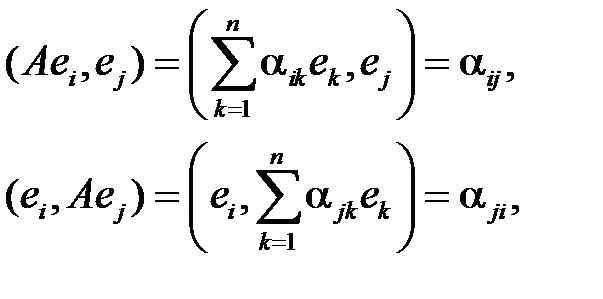
т. е., в виду (7.7)

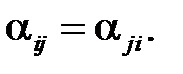
Матрица A, таким образом, оказалась симметричной.

Обратно, линейное преобразование евклидова пространства в ортонормированном базисе e ₁, e ₂,…, e_n задаетсясимметричной матрицей.

Пусть

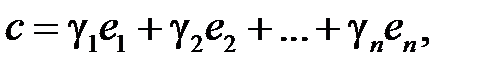
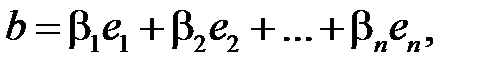
тогда

Используя ортонормированность базиса, получаем

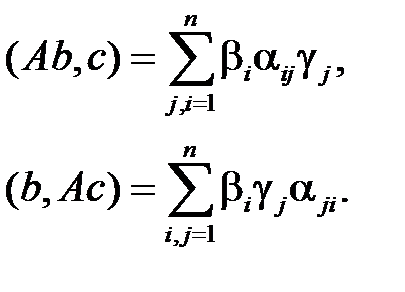
Правые части совпадают, и поэтому

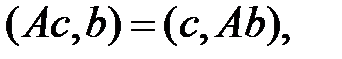
тем самым теорема доказана.

Теорема7.4. Все характеристические корни симметрической матрицы действительны.

Доказательство. Пусть А − симметричная квадратная матрица порядка n с действительными коэффициентами, 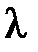− характеристический корень (быть может, комплексный) матрицы 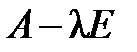. Тогда характеристический корень удовлетворяет системе однородных уравнений

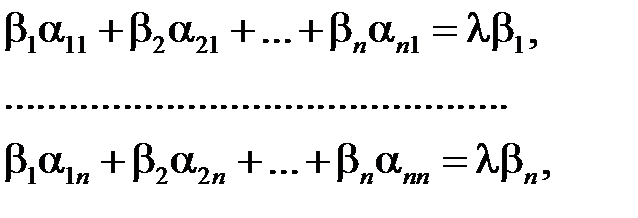
где собственный вектор

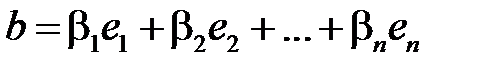
соответствует собственному значению 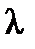с матрицей преобразования А.

Умножая обе части каждого равенства на число, сопряженное с 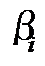и складывая все равенства, имеем:

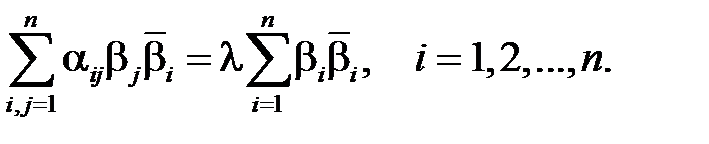
Коэффициент при 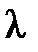есть действительное число, как сумма произведений сопряженных чисел. Чтобы доказать действительность числа 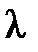достаточно показать, что оно совпадает с сопряженным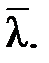

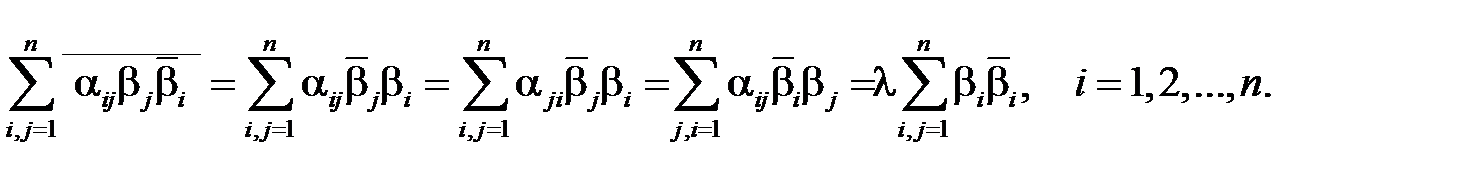
При доказательстве воспользовались действительностью и симметричностью матрицы A. В результате получили

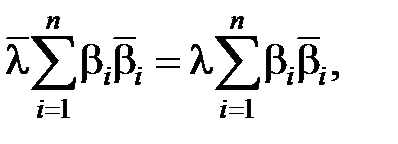
т.е. 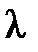есть действительное число.

Теорема 7. 5. Собственные векторы симметрического преобразования A, относящиеся к различным собственным значениям, между собой ортогональны.

Доказательство. Пусть

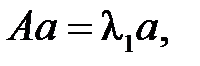
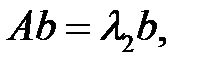
Т. к.

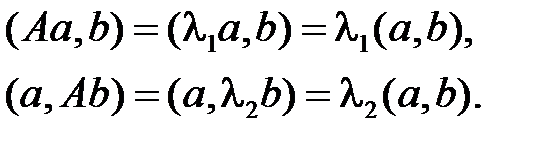
из определения симметрического преобразования

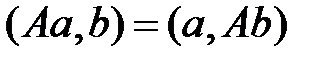
следует

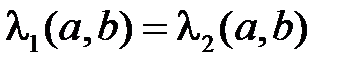
или, ввиду 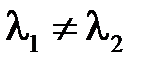, получаем (a, b) = 0, что и требовалось доказать.

Пусть существует ортонормированный базис линейного преобразования A из собственных векторов

Примем e ₁, e _{2, …}, e_n за базис, тогда матрица преобразования А в этом базисе имеет диагональный вид

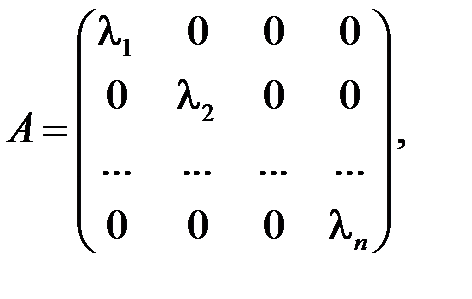
т.е. преобразование A является симметричным.

В заключении отметим, что линейное преобразование евклидова пространства, тогда и только тогда, будет симметричным, если в пространстве существует ортонормированный базис, составленный из собственных векторов этого преобразования.