Прямая линия на плоскости. Основные задачи

Угол между прямыми на плоскости

O

a1

a2

j

j

y

x

L 1

L 2

Рис. 25

Рассмотрим две прямые L ₁ и L ₂ с угловыми коэффициентами y = k ₁ x + b ₁, y = k ₂ x + b ₂ (рис. 26). Требуется найти угол j, на который надо повернуть прямую L ₁ вокруг точки их пересечения до совпадения с прямой L ₂.

Из геометрических соображений устанавливаем зависимость между углами a₁, a₂, j: a₂ = a₁ + j или j = a₂ - a₁ (j ¹ p/2). Отсюда

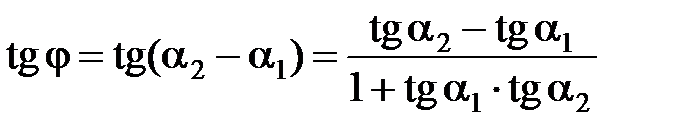, или

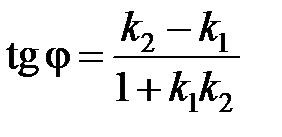. (3.12)

Если требуется вычислить острый угол между прямыми, не учиты­вая, какая прямая является первой, какая - второй, то правая часть фор­му­лы (3.12) берется по модулю.

Если две прямые параллельны, то j = 0 и tg j = 0. Из формулы (3.12) следует, что k ₁ = k ₂ - условие параллельности двух прямых.

Если две прямые перпендикулярны, то j = p/2. Следовательно, 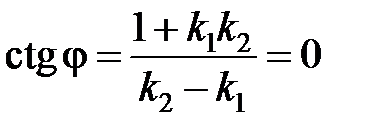. Отсюда 1 + k ₁ k ₂ = 0, т. е. k ₁ k ₂ = -1 (или k ₁ = -1/ k ₂) - усло­вие перпендикулярности двух прямых.

Теорема 3.1. Прямые Ах + Ву + С = 0 и А ₁ х + В ₁ у + С ₁ = 0 пара­л­лельны, когда пропорциональны коэффициенты А ₁ = l А, В ₁ = l В. Если еще и С ₁ = l С, то прямые совпадают.

Координаты точки пересечения двух прямых находятся как решение системы двух уравнений.

Расстояние от точки до прямой

Теорема3.2. Если задана точка М ₀(х ₀, у ₀), то расстояние до пря­мой Ах + Ву + С = 0 определяется как

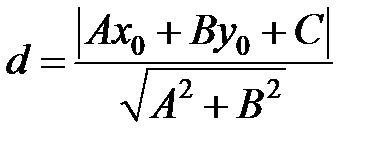. (3.13)

M 0

O

y

x

L

M 1

d

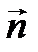
Рис. 26

Доказательство. Пусть М ₁(х ₁; у ₁) - произвольная точка пря­мой L, нормальный вектор прямой имеет коорди­наты (А; В). Определим расстояние d от точки M ₀ до прямой L (рис. 26)

.

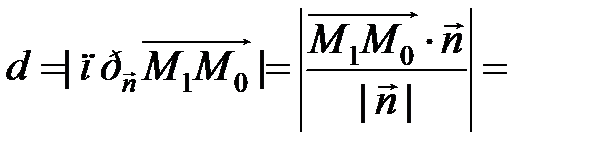
Т. к. М ₁ Î L: Ax ₁ + By ₁ + C = 0, т. е. C = - Ax ₁ - By ₁, то

.

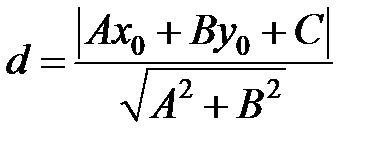Теорема доказана.

Пример 9. Определить угол между прямыми: y = -3 x +7; y = 2 x +1.

Решение.

k ₁ = -3, k ₂ = 2, tg j = 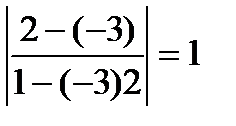; j = p/4.

Пример 10. Показать, что прямые 3 х – 5 у + 7 = 0 и 10 х + 6 у – 3 = 0 перпендикулярны.

Находим: k ₁ = 3/5, k ₂ = -5/3, k ₁ k ₂ = -1, следовательно, прямые перпендикулярны.

Пример 11. Даны вершины треугольника А (0; 1), B (6; 5), C (12; -1). Найти уравнение высоты CH и уравнение CL биссектрисы, проведенной из вершины С.

По (3.8) находим уравнение стороны АВ: 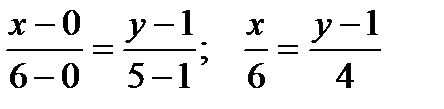; 4 x = 6 y – 6;

2 x – 3 y + 3 = 0;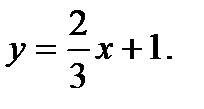

Искомое уравнение высоты CH имеет вид: Ax + By + C = 0 или y = kx + b. Угловой коэффициент k = 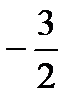. Тогда y = 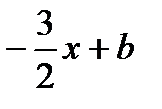. Т. к. высота проходит через точку С, то ее координаты удовлетворяют данному уравнению: 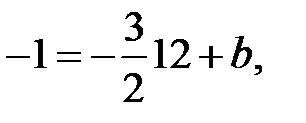откуда b = 17. Итак, 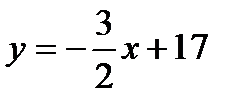или 3x + 2y – 34 = 0.

У биссектрисы CL найдем координаты точки L. По свойству биссектрисы 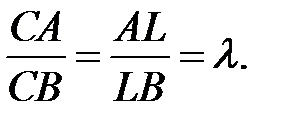Вычисляя длины соответствующих векторов, находим 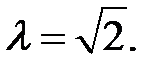Тогда по формуле (2.10) находим координаты точки L:

,

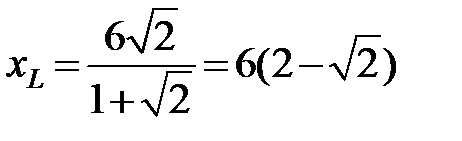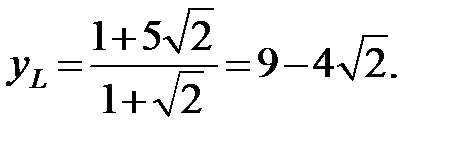
Уравнение биссектрисы 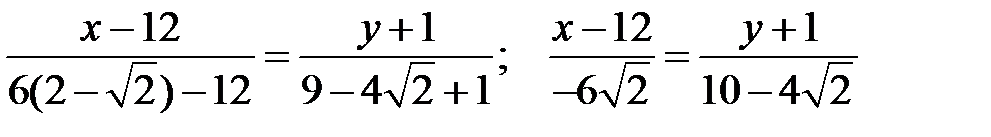. Итак, уравнение биссектрисы