 |
Главная Случайная страница Контакты | Мы поможем в написании вашей работы! | |
Понятие вектора. Линейные операции над векторами и их основные свойства
|
|
Основные понятия
Определение. Вектором называется направленный прямолинейный отрезок (упорядоченная пара точек). К векторам относится также и нулевой вектор, начало и конец которого совпадают. Если А - начало вектора, а В - его конец, то вектор обозначается символом 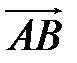 или
или 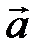 . Вектор
. Вектор 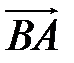 называется противоположным вектору
называется противоположным вектору 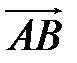 . Вектор, противоположный вектору
. Вектор, противоположный вектору 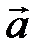 , обозначается -
, обозначается - 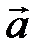 .
.
Определение. Длиной (модулем) вектора называется расстояние между началом и концом вектора
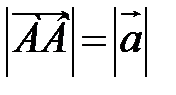 .
.
Определение. Векторы называются коллинеарными, если они расположены на одной или параллельных прямых, обозначается 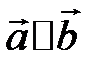 . Нулевой вектор коллинеарен любому вектору.
. Нулевой вектор коллинеарен любому вектору.
Определение. Векторы называются компланарными, если существует плоскость, которой они параллельны.
Коллинеарные векторы всегда компланарны, но не все компланарные векторы коллинеарны.
Определение. Векторы называются равными ( ), если они коллинеарны, одинаково направлены и имеют одинаковые длины.
), если они коллинеарны, одинаково направлены и имеют одинаковые длины.
Всякие векторы можно привести к общему началу, т. е. построить векторы, соответственно равные данным и имеющие общее начало. Из определения равенства векторов следует, что любой вектор имеет бесконечно много векторов, равных ему.
Определение. Вектор 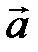 называется единичным или ортом, если
называется единичным или ортом, если 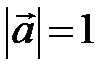 . Обозначается
. Обозначается 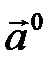 .
.
Определение. Вектор 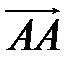 , начало и конец которого находятся в одной точке, называется нулевым и обозначается
, начало и конец которого находятся в одной точке, называется нулевым и обозначается 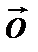 . Длина нулевого вектора
. Длина нулевого вектора 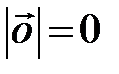 , направление не определено.
, направление не определено.
Линейные операции над векторами
Определение. Линейными операциями над векторами называется сложение, вычитание, а также умножение вектора на число.
Определение. Суммой двух векторов 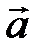 и
и 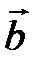 является вектор
является вектор 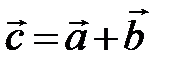 (рис. 1).
(рис. 1).
| О |
| А |
| В |
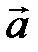 А А
|
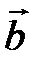 А А
|
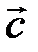 А А
|
Рис. 1.
Такое правило сложения векторов называют правилом треугольника.
Сумму векторов можно построить также по правилу параллелограмма (рис. 2).
| О |
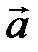 О О
|
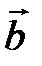 О О
|
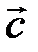 О О
|
Рис. 2.
Определение. Разностью двух векторов 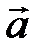 и
и 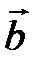 называется такой вектор
называется такой вектор 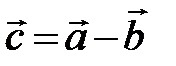 , что
, что 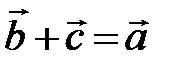 (рис. 3).
(рис. 3).
| О |
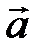 |
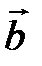 О О
|
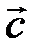 О О
|
Рис. 3
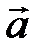
|
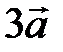
|
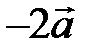
|
| Рис. 4 |
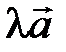 вектора
вектора 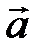 на число l называется вектор
на число l называется вектор 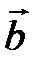 , коллинеарный вектору
, коллинеарный вектору 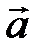 , имеющий длину, равную
, имеющий длину, равную 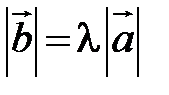 , и направление, совпадающее с направлением
, и направление, совпадающее с направлением 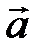 при l > 0 и противоположное
при l > 0 и противоположное 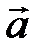 при l < 0 (рис. 4). Если l = 0 или
при l < 0 (рис. 4). Если l = 0 или 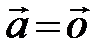 , то
, то 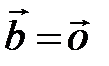 .
.Свойства линейных операций над векторами
Для произвольных векторов 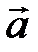 ,
,  ,
, 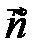 и любых действительных чисел a, b выполняются следующие равенства:
и любых действительных чисел a, b выполняются следующие равенства:
1) 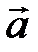 +
+  =
=  +
+ 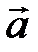 ;
;
2) 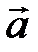 + (
+ ( +
+ 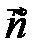 ) = (
) = (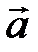 +
+  ) +
) + 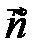 ;
;
3) 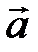 +
+ 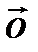 =
= 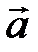 ;
;
4) 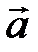 + (-1)
+ (-1) 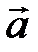 =
= 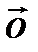 ;
;
5) (a×b) 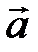 = a(b
= a(b 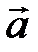 );
);
6) (a+b) 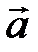 = a
= a 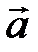 + b
+ b 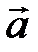 ;
;
7) a(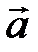 +
+  ) = a
) = a 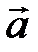 + a
+ a  ;
;
8) 1× 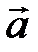 =
= 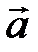 .
.
Линейная зависимость векторов
Определение. Линейной комбинацией векторов 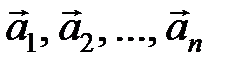 называется вектор
называется вектор 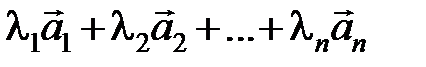 , где числа l1, l2, …, l n называются коэффициентами этой линейной комбинации.
, где числа l1, l2, …, l n называются коэффициентами этой линейной комбинации.
Определение. Вектора 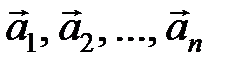 называются линейно зависимыми, если хотя бы один из векторов системы может быть выражен как линейная комбинация остальных.
называются линейно зависимыми, если хотя бы один из векторов системы может быть выражен как линейная комбинация остальных.
Итак, вектора 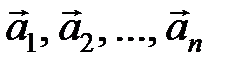 линейно зависимы, если, например,
линейно зависимы, если, например,
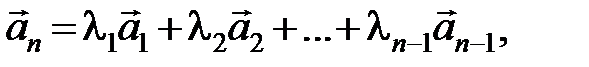 (2.1)
(2.1)
где l1, l2, …, l n -1 - некоторые числа.
Определение. Вектора 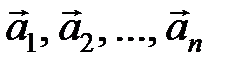 называются линейно зависимыми, если существуют числа l1, l2, …, l n, из которых хотя бы одно отлично от нуля, такие, что
называются линейно зависимыми, если существуют числа l1, l2, …, l n, из которых хотя бы одно отлично от нуля, такие, что
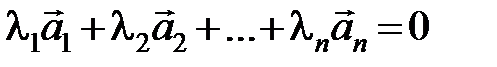 . (2.2)
. (2.2)
Это определение равносильно предыдущему. Действительно, если в равенстве (2.1) 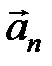 перенести в правую часть, то получим
перенести в правую часть, то получим 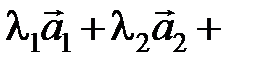 …
… 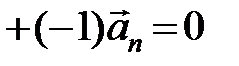 , и, следовательно, имеем равенство (2.2). Допустим в равенстве (2.2) l n ¹ 0, тогда вектор
, и, следовательно, имеем равенство (2.2). Допустим в равенстве (2.2) l n ¹ 0, тогда вектор 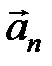 может быть выражен как линейная комбинация остальных векторов
может быть выражен как линейная комбинация остальных векторов
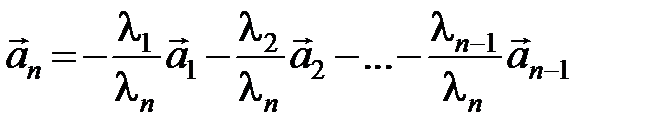 ,
,
и, значит, выполнено условие (2.1).
Определение. Вектора 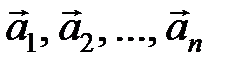 называются линейно независимыми, если равенство (2.2) выполняется только при l1= l2= … = l n = 0.
называются линейно независимыми, если равенство (2.2) выполняется только при l1= l2= … = l n = 0.
Замечание. Если среди векторов 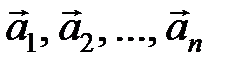 имеется хотя бы один нулевой вектор, то вектора
имеется хотя бы один нулевой вектор, то вектора 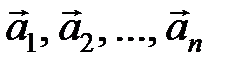 линейно зависимы.
линейно зависимы.
Замечание. Если среди n векторов какие-либо (n - 1) линейно зависимы, то и все n векторов линейно зависимы.
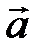
|
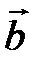
|
| Рис. 5 |
Действительно, поместим векторы 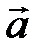 и
и 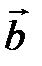 на одной прямой, тогда можно найти такое число l, при котором
на одной прямой, тогда можно найти такое число l, при котором  Þ
Þ 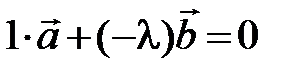 , т. е. вектора
, т. е. вектора 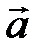 и
и 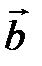 линейно зависимы.
линейно зависимы.
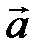
|
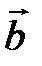
|
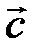
|
| Рис. 6 |
Действительно, поместим начало трех векторов в общую точку. Очевидно, что тогда можно подобрать единственную пару чисел l1 и l2, так, чтобы выполнялось следующее равенство 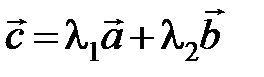 , т. е. вектора
, т. е. вектора 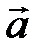 ,
, 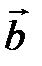 и
и  линейно зависимы.
линейно зависимы.
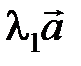
|
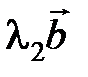
|
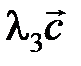
|
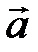
|
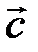
|
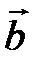
|
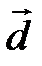
|
| Рис. 7 |
Действительно, поместим начало четырех векторов в общую точку. Можно подобрать, причем единственным образом, числа l1, l2 и l3, так, чтобы выполнялось следующее равенство 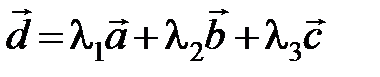 , т. е. вектора
, т. е. вектора 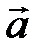 ,
, 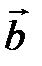 ,
,  и
и 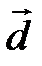 линейно зависимы.
линейно зависимы.
Базис. Координаты вектора в базисе
Определение. Базисом на прямой называется любой ненулевой вектор, принадлежащий этой прямой. Базисом на плоскости называются любые два неколлинеарных вектора, взятые в определенном порядке. Базисом в пространстве называются любые три некомпланарных вектора, взятые в определенном порядке.
Определение. Базис называется ортогональным, если образующие его вектора попарно перпендикулярны. Ортогональный базис называется ортонормированным, если образующие его вектора имеют единичную длину.
Теорема2.1 Любой вектор 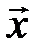 в пространстве с базисом
в пространстве с базисом 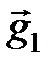 ,
, 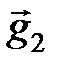 ,
, 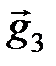 может быть представлен, причем единственным способом, в виде
может быть представлен, причем единственным способом, в виде 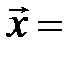
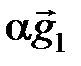 +
+ 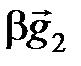 +
+ 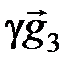 , где a, b, g - некоторые числа.
, где a, b, g - некоторые числа.
| О |
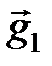
|
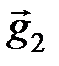
|

|
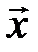
|
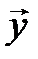
|
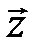
|
| Рис. 8 |
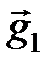 ,
, 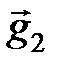 ,
, 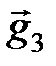 и
и 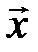 в точке О и проведем через конец вектора
в точке О и проведем через конец вектора 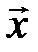 плоскость, параллельную плоскости
плоскость, параллельную плоскости 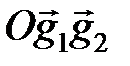 (рис. 8).
(рис. 8).
Построим новые вектора  и
и  так, чтобы
так, чтобы 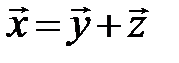 , и при этом вектора
, и при этом вектора  и
и 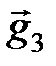 были бы коллинеарны, т. е. выполнялось бы равенство
были бы коллинеарны, т. е. выполнялось бы равенство 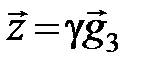 .
.
Перенесем вектор  в точку О, тогда
в точку О, тогда 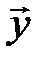 =
= 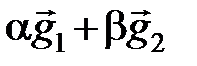 , и, следовательно,
, и, следовательно, 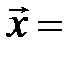
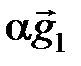 +
+ 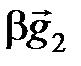 +
+ 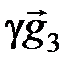 , что и доказывает существование таких чисел.
, что и доказывает существование таких чисел.
Докажем единственность разложения по данному базису. Предположим, что существуют два различных разложения вектора  в базисе
в базисе 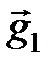 ,
, 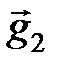 ,
, 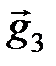
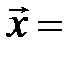
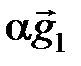 +
+ 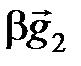 +
+ 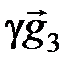 и
и 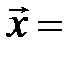
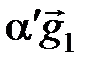 +
+ 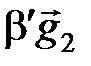 +
+ 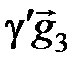 .
.
Вычитая почленно эти равенства, получим
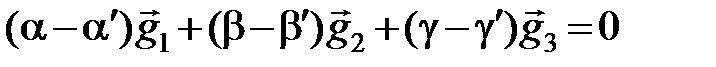 ,
,
где в силу сделанных предположений 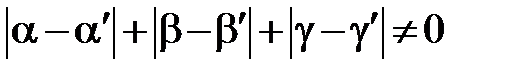 . Но это условие и означает, что вектора
. Но это условие и означает, что вектора 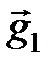 ,
, 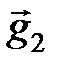 ,
, 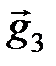 являются линейно зависимыми и не могут образовывать базис. Это, в свою очередь, доказывает единственность разложения.
являются линейно зависимыми и не могут образовывать базис. Это, в свою очередь, доказывает единственность разложения.
Определение. Числа a, b, g в разложении 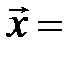
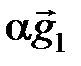 +
+ 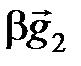 +
+ 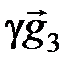 называются координатами вектора
называются координатами вектора  в базисе
в базисе 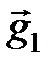 ,
, 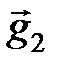 ,
, 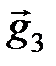 . Записываются в виде строки
. Записываются в виде строки 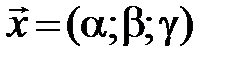 .
.
Свойства базиса
1. При сложении векторов их координаты относительно любого базиса складываются;
2. При умножении вектора на число все его координаты умножаются на это число.
Переход к новому базису. Поскольку векторное пространствоможет иметь не единственный базис встает вопрос, о переходе от разложения в одном базисе к разложению в другом базисе. Пусть имеется два базиса:  и
и 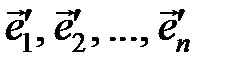 , и пусть некоторый вектор раскладывается по базисам
, и пусть некоторый вектор раскладывается по базисам 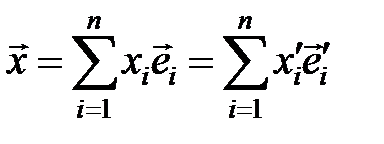 . Очевидно, что векторы «нового» базиса
. Очевидно, что векторы «нового» базиса 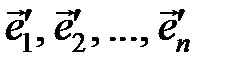 также можно разложить по «старому» базису
также можно разложить по «старому» базису 
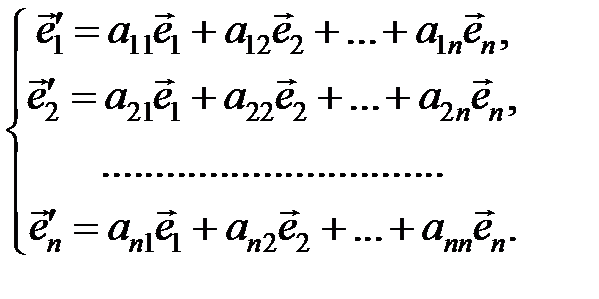
Составим матрицу перехода А от «старого» базиса к «новому»
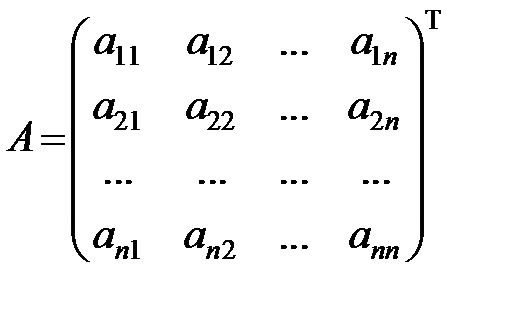 ,
, 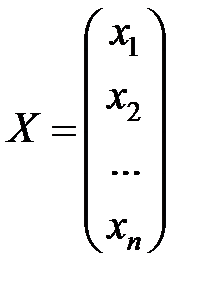 ,
, 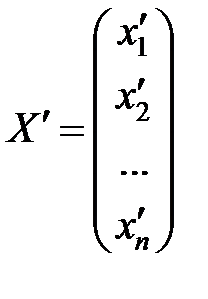 ,
,
тогда X = А × X ′или обратное соотношение X ′ = А −1× X.
Матрица А называется матрицей преобразования координат при переходе от базиса  к базису
к базису 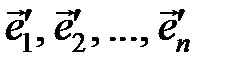 .
.
Пример1.Координаты вектора 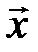 = (6;6;1) даны в базисе
= (6;6;1) даны в базисе 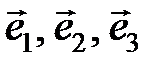 . Записать его координаты в базисе
. Записать его координаты в базисе 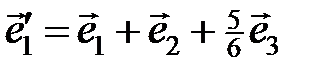 ,
, 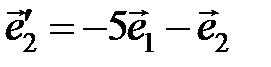 ,
, 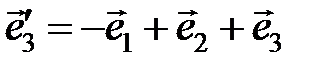 .
.
Решение. Запишем матрицу перехода
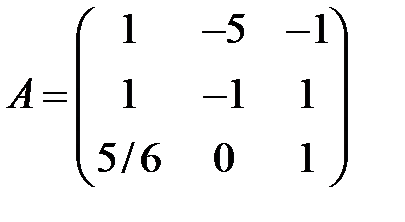 .
.
Строим обратную матрицу det(A) = -1 ¹ 0, поэтому
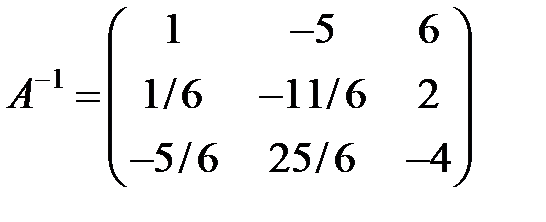 .
.
Тогда 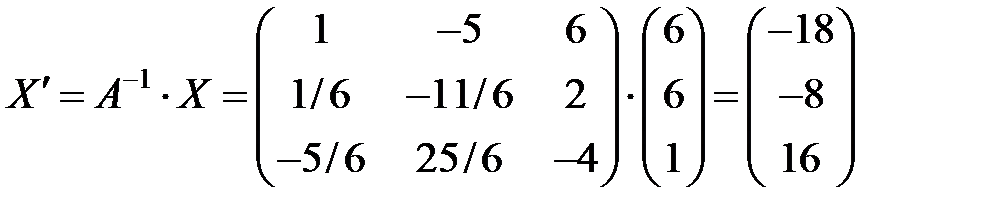 или
или
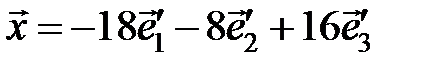 .
.
Пример2. В базисе 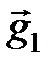 ,
, 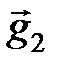 ,
, 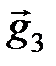 заданы три вектора
заданы три вектора 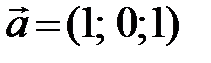 ,
, 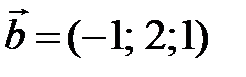 ,
, 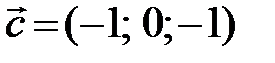 . В базисе
. В базисе 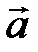 ,
, 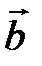 ,
, 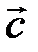 задан вектор
задан вектор 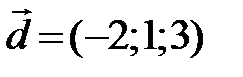 . Найти координаты вектора
. Найти координаты вектора 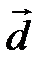 в базисе
в базисе 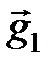 ,
, 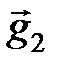 ,
, 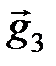 .
.
Решение. Вектор 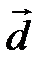 разложим по векторам базиса
разложим по векторам базиса 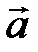 ,
, 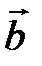 ,
, 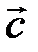 :
: 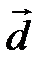 = -2
= -2 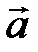 +
+ 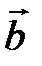 +3
+3 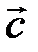 , а вектора
, а вектора 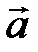 ,
, 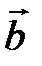 ,
, 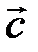 по векторам базиса
по векторам базиса 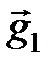 ,
, 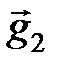 ,
, 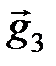 :
: 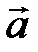 =
= 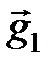 +
+ 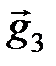 ,
, 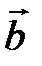 = -
= - 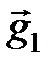 +2
+2 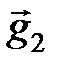 +
+ 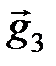 ,
, 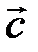 = -
= - 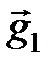 -
- 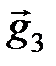 . Подставим в разложение вектора
. Подставим в разложение вектора 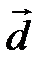 последние равенства, получим
последние равенства, получим 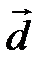 = -2(
= -2(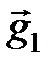 +
+ 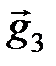 ) -
) - 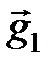 +2
+2 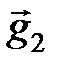 +
+ 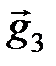 + 3(-
+ 3(- 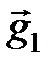 -
- 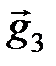 ) = -6
) = -6 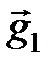 + 2
+ 2 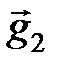 - 4
- 4 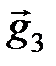 .
.
В базисе 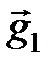 ,
, 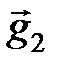 ,
, 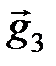 вектор
вектор 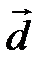 = (-6; 2; -4).
= (-6; 2; -4).
Пример3. Выяснить, являются ли линейно зависимыми векторы 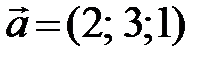 ,
, 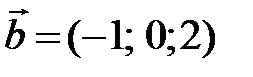 ,
, 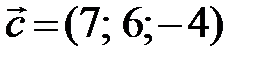 и, если это так, выразить один из векторов через другие.
и, если это так, выразить один из векторов через другие.
Решение. Проверим условие линейной зависимости векторов 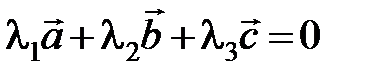
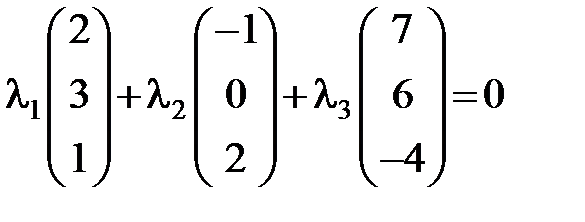 или
или 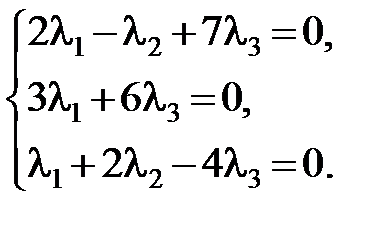
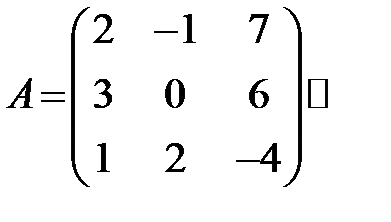
| -3 |
| -2 |
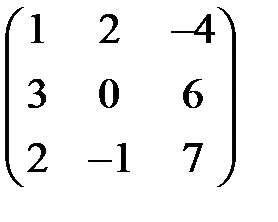
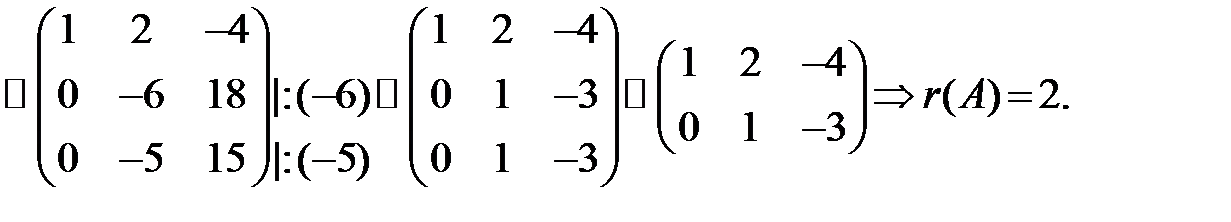
Т. к. r (A) = 2, система имеет линейно зависимые строки. Выразим один вектор через другие. Положим l3 = 1, тогда l2 = 3, l1 = -2, 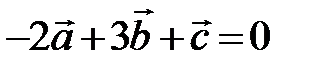 ,
, 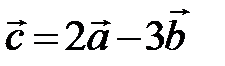 .
.
Проекция вектора на ось
| x |
| y |
| z |
| O |
| M |
| Mx |
| My |
| Mz |
|

|
|
| Рис. 9 |
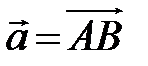 . Проектируя начало и конец вектора на ось l, получим вектор
. Проектируя начало и конец вектора на ось l, получим вектор 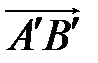 (рис. 9).
(рис. 9).
| l |
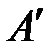
|
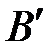
|
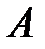
|
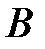
|
| Рис. 10 |
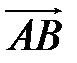 на ось l называется число, равное длине вектора
на ось l называется число, равное длине вектора 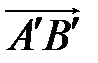 , взятой со знаком «+» или «-» в зависимости от того, направлен ли вектор
, взятой со знаком «+» или «-» в зависимости от того, направлен ли вектор 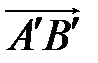 в ту же сторону, что и ось l, или противоположную. Обозначается
в ту же сторону, что и ось l, или противоположную. Обозначается 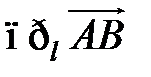 .
.
Определение. Углом между двумя векторами называется наименьший угол, на который надо повернуть один из векторов, чтобы его направление совпало с направлением другого вектора.
| А |
| В |

|
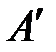
|
| l |
| j |
| Рис. 11 |
| B 1 |
1.  , где j - угол между векторами
, где j - угол между векторами 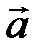 и
и 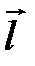 (рис. 10).
(рис. 10).
2. 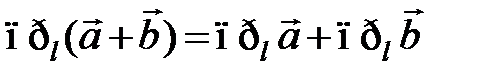 .
.
3. 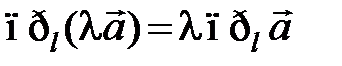 , где l некоторое числ о.
, где l некоторое числ о.
Определение. Прямоугольной д екартовой системой координат в пространстве называется совокупность точки и ортонормированного базиса. Точка называется началом координат. Прямые, проходящие через начало координат, называются осями координат: 1-я ось – ось абсцисс, 2-я ось – ось ординат, 3-я ось – ось аппликат. Плоскости, проходящие через оси координат, называются координатными плоскостями.
Зафиксируем в пространстве точку О, проведем через нее три взаимно перпендикулярные оси, на каждой из них возьмем единичный вектор, направленный по этой оси 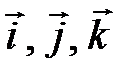 (орт оси) и рассмотрим произвольную точку М (рис. 11).
(орт оси) и рассмотрим произвольную точку М (рис. 11).
Вектор 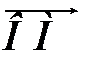 назовем радиус-вектором точки М. Если в пространстве задать некоторый базис, то точке М можно сопоставить некоторую тройку чисел – координаты ее радиус-вектора. Проектируя точку М на ось Ох, получим точку Мх. Первой координатой х или абсциссой точки М называется длина вектора
назовем радиус-вектором точки М. Если в пространстве задать некоторый базис, то точке М можно сопоставить некоторую тройку чисел – координаты ее радиус-вектора. Проектируя точку М на ось Ох, получим точку Мх. Первой координатой х или абсциссой точки М называется длина вектора 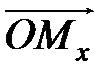 , взятая со знаком «+», если
, взятая со знаком «+», если 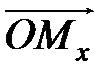 направлен в ту же сторону, что и вектор
направлен в ту же сторону, что и вектор 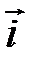 , и со знаком «-» - если в противоположную. Аналогично получим точки My, Mz и определим ординату у и аппликату z точки М. Таким образом, имеем
, и со знаком «-» - если в противоположную. Аналогично получим точки My, Mz и определим ординату у и аппликату z точки М. Таким образом, имеем
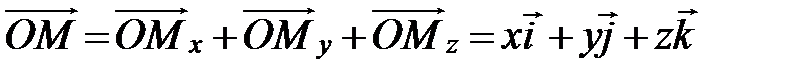 .
.
Такое представление вектора 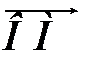 называется разложением его на компоненты или составляющие по координатным осям. Нетрудно заметить, что вектор
называется разложением его на компоненты или составляющие по координатным осям. Нетрудно заметить, что вектор 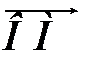 лежит на диагонали параллелепипеда, следовательно, можно найти его длину
лежит на диагонали параллелепипеда, следовательно, можно найти его длину
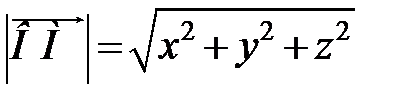 . (2.3)
. (2.3)
Координаты вектора 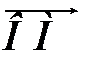 обозначаются
обозначаются  или
или 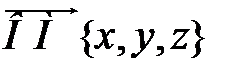 . Координаты точки М записывают так: M (x, y, z).
. Координаты точки М записывают так: M (x, y, z).
Пусть углы вектора 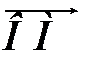 с осями Ox, Oy и Oz соответственно равны a, b, g. По свойству проекции вектора на ось, имеем
с осями Ox, Oy и Oz соответственно равны a, b, g. По свойству проекции вектора на ось, имеем
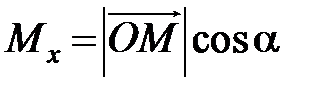 ,
, 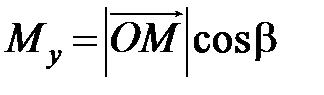 ,
, 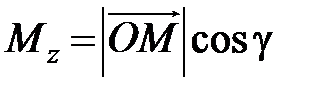 ,
,
или
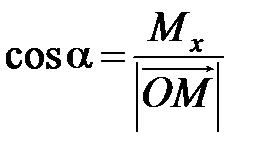 ,
, 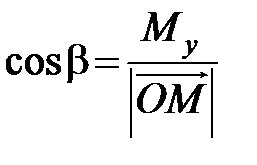 ,
, 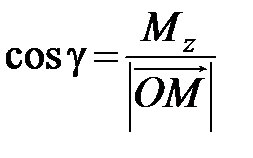 . (2.4)
. (2.4)
Числа 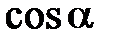 ,
, 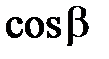 ,
, 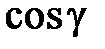 называются направляющими косинусами вектора
называются направляющими косинусами вектора 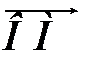 .
.
Направляющие косинусы связаны между собой соотношением
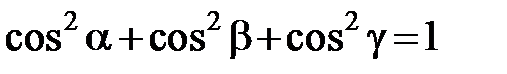 . (2.5)
. (2.5)
Единичный вектор 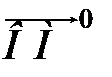 , соответствующий вектору
, соответствующий вектору 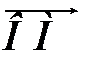 , равен
, равен 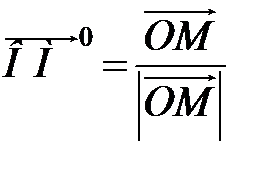 . Нетрудно заметить, что координаты единичного вектора совпадают с его направляющими косинусами.
. Нетрудно заметить, что координаты единичного вектора совпадают с его направляющими косинусами.
Если даны координаты точек А (x 1, y 1, z 1) и B (x 2, y 2, z 2), то координаты вектора 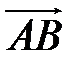 =
= 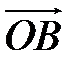 −
− 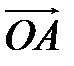 получаются вычитанием из координат его конца В координат начала А
получаются вычитанием из координат его конца В координат начала А
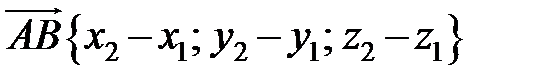 , или
, или
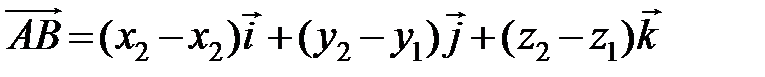 . (2.6)
. (2.6)
При сложении (вычитании) векторов их координаты складываются (вычитаются), при умножении вектора на число все его координаты умножаются на это число, т. е. если
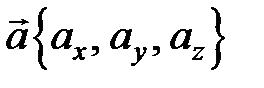 и
и 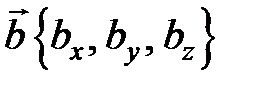 ,
,
то
 ,
,
 . (2.7)
. (2.7)
Если векторы 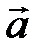 и
и 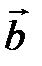 коллинеарны, то они отличаются друг от друга скалярным множителем, т. е.
коллинеарны, то они отличаются друг от друга скалярным множителем, т. е.  . Из (2.7) следует, что у коллинеарных векторов координаты пропорциональны
. Из (2.7) следует, что у коллинеарных векторов координаты пропорциональны
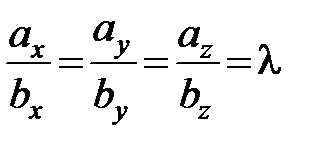 . (2.8)
. (2.8)
Равенство (2.8) называется условием коллинеарности двух векторов.
Длина вектора 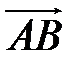 , заданного координатами своих концов, т. е. расстояние между точками А и В вычисляется по формуле
, заданного координатами своих концов, т. е. расстояние между точками А и В вычисляется по формуле
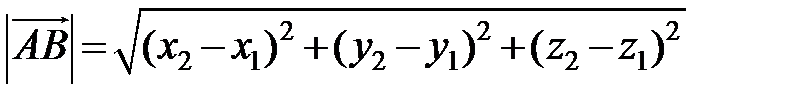 . (2.9)
. (2.9)
Деление отрезка в данном отношении
Найдем координаты точки М (x, y, z) на отрезке АВ, которая делит этот отрезок в отношении l (рис. 12), т. е. удовлетворяет условию
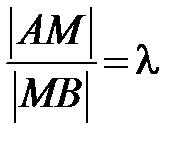 (l > 0).
(l > 0).
Это условие можно переписать в виде
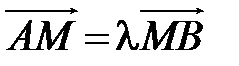 .
.
Выпишем координаты векторов 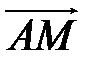 и
и 
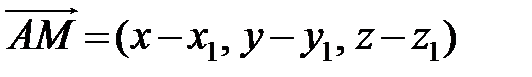 ,
, 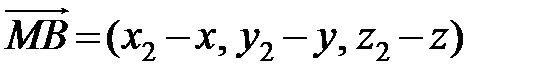 .
.
Тогда
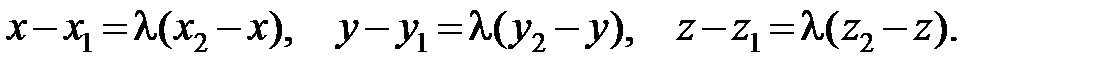
Из этих равенств можно найти x, y, z
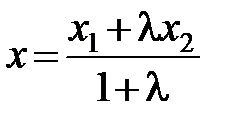 ,
, 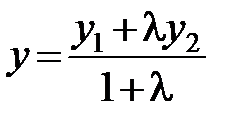 ,
, 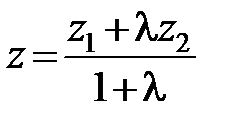 . (2.10)
. (2.10)
Формулы (2.10) известны под названием формул деления отрезка в данном отношении.
Из формул (2.10) получается, что координаты середины отрезка (l = 1) равны полусуммам соответствующих координат концов
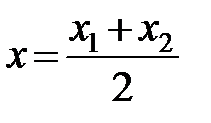 ,
, 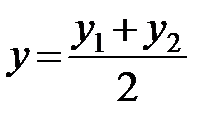 ,
, 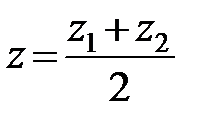 .
.
| А |
| М |
| В |
| Рис. 12 |
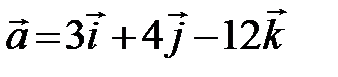 .
.
Решение. Координаты вектора 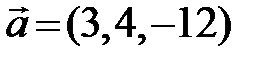 . Определим длину вектора
. Определим длину вектора 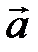 , используя формулу (2.3)
, используя формулу (2.3)
 .
.
Направление вектора 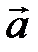 определяют направляющие косинусы, из соотношений (2.4) имеем
определяют направляющие косинусы, из соотношений (2.4) имеем
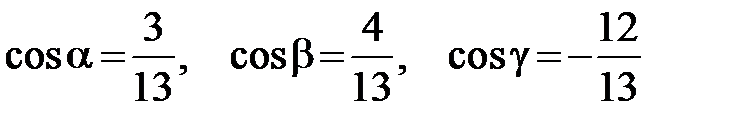 .
.
Пример5. Вектор 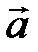 составляет с осями координат острые углы a, b, g, причем
составляет с осями координат острые углы a, b, g, причем  ,
, 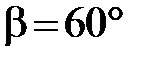 . Найти его координаты, если
. Найти его координаты, если 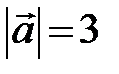 .
.
Решение. Прежде всего, из соотношения (2.5) найдем угол g
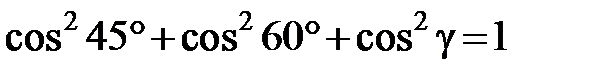 ,
,
 Þ
Þ 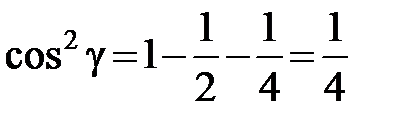 .
.
Т. к. по условию угол g острый, то 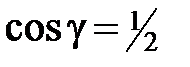 и
и 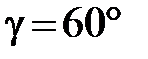 . Следовательно,
. Следовательно,
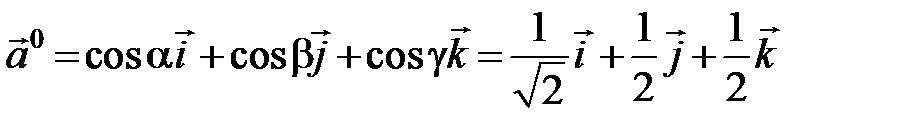 ,
,
поэтому
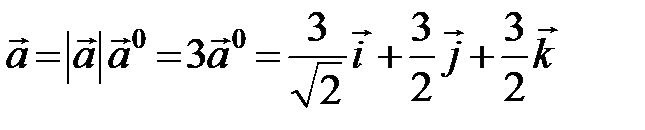 или
или 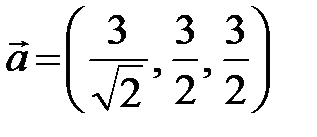 .
.
Пример6. Коллинеарны ли векторы 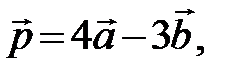
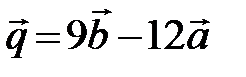 , где
, где 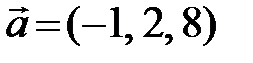 и
и 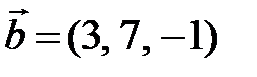 ?
?
Решение. Найдем координаты векторов  и
и 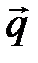 , используя формулы (2.7)
, используя формулы (2.7)
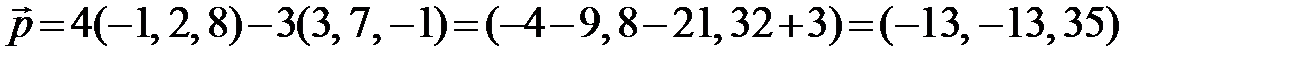 ,
,
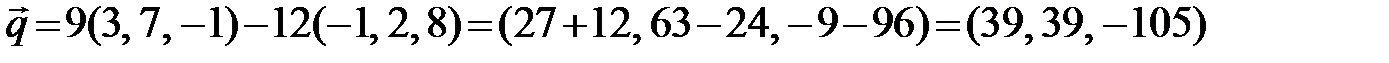 .
.
Проверим условие (2.8) коллинеарности двух векторов
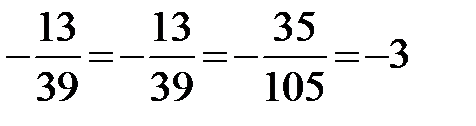 ,
,
т. к., координаты пропорциональны, следовательно, векторы  и
и 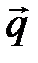 коллинеарны.
коллинеарны.
Пример7. Определить координаты вектора 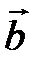 , если известно, что
, если известно, что 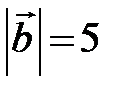 , он коллинеарен вектору
, он коллинеарен вектору 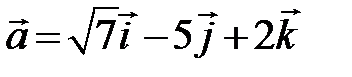 и его направление совпадает с направлением вектора
и его направление совпадает с направлением вектора 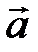 .
.
Решение. Обозначим координаты вектора 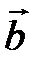 через x, y, z, т. е.
через x, y, z, т. е. 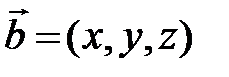 . Поскольку векторы коллинеарны, то
. Поскольку векторы коллинеарны, то 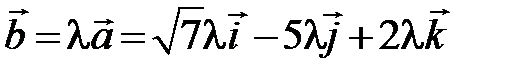 . Из равенства векторов
. Из равенства векторов 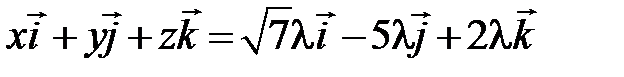 следует равенство их координат
следует равенство их координат 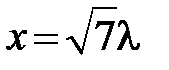 ,
, 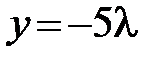 ,
,  . Т. к.
. Т. к. 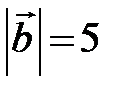 , то по формуле (2.3) имеем
, то по формуле (2.3) имеем
 , или
, или 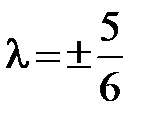 .
.
Поскольку направления векторов 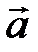 и
и 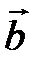 совпадают, то следует взять l > 0, т. е.
совпадают, то следует взять l > 0, т. е. 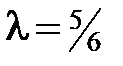 . Значит, координаты искомого вектора будут
. Значит, координаты искомого вектора будут
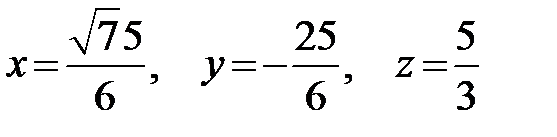 .
.
1. Пример8. Даны координаты вершин треугольника ABC: А (0;4), В (−2;2), С (6;0). Найти координаты точки G - точки пересечения медиан (центра масс треугольной однородной пластины) АВС.
Решение. Пусть AM – медиана треугольника ABC. Точка М, как середина отрезка ВС имеет координаты М (2;1), вектор 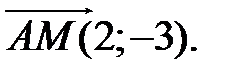 Так как в точке пересечения медиан выполняется соотношение
Так как в точке пересечения медиан выполняется соотношение 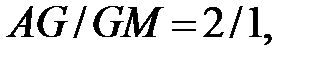 то
то 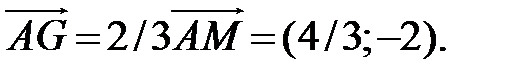 Из векторного равенства
Из векторного равенства 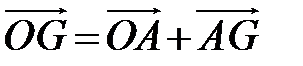 находим G (4/3;2).
находим G (4/3;2).
Дата публикования: 2014-11-04; Прочитано: 1598 | Нарушение авторского права страницы | Мы поможем в написании вашей работы!
