 |
Главная Случайная страница Контакты | Мы поможем в написании вашей работы! | |
Теорема Стокса
|
|
(устанавливает связь между циркуляцией и ротором)
Циркуляция непрерывно дифференцируемого векторного поля 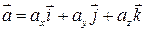 по произвольному кусочно-гладкому контуру L вычисляется по формуле
по произвольному кусочно-гладкому контуру L вычисляется по формуле
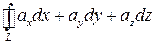 =
= 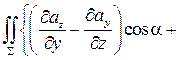
+ 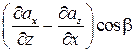 +
+  .
.
При этом выбор стороны поверхности  и направление обхода контура L согласованы (по правилу винта).
и направление обхода контура L согласованы (по правилу винта).
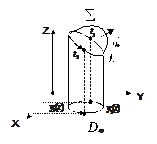 Доказательство:
Доказательство:
Для доказательства сгруппируем слагаемые в правой части с одинаковыми координатами вектора 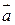 :
:
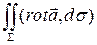 =
= 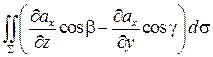 +
+
+ 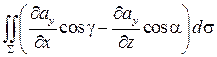 +
+
+ 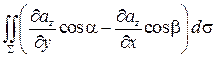 .
.
Рассмотрим первый из интегралов:
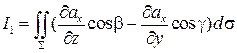 =
= 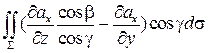 .
.
Пусть поверхность 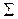 является такой, что любая прямая пересекает ее лишь в одной точке, тогда
является такой, что любая прямая пересекает ее лишь в одной точке, тогда  :
: 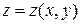 ;
; 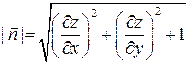 ;
; 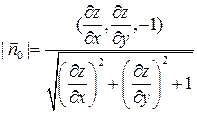 , тогда
, тогда 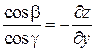 , так как
, так как 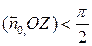 ;
; 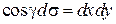 . Переходя к двойному интегралу по Dxy:
. Переходя к двойному интегралу по Dxy: 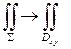 , получим
, получим
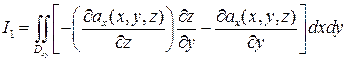 .
.
По формуле дифференцирования сложной функции, записывая полную производную сложной функции, имеем:
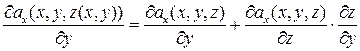 ,
,
 = =
= = 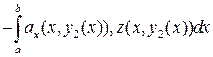 +
+
+  =
=  .
.
Докажем последнее преобразование.

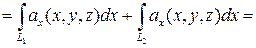 …
…
{пусть L задана параметрически}…
= 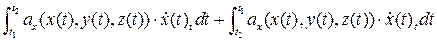 =
=
…{ 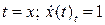 }…=
}…=
=  .
.
Остальные два слагаемых рассматриваются аналогично. Почленное суммирование этих выражений приводит к формуле Стокса.
1). Используя обозначение ротора, формулу Стокса можно переписать в векторном виде:  =
= 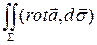 . Поток вектора
. Поток вектора 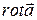 через ориентированную поверхность
через ориентированную поверхность  равен циркуляции поля
равен циркуляции поля 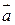 по контуру L, ориентированному в соответствии с ориентацией
по контуру L, ориентированному в соответствии с ориентацией  .
.
2). Для того чтобы криволинейный интеграл по любому кусочно-гладкому контуру равнялся нулю, необходимо и достаточно, чтобы выполнялись условия Стокса: 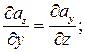
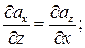
 .
.
ПРИМЕР  . Вычислите циркуляцию вектора
. Вычислите циркуляцию вектора 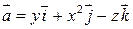 по контуру L:
по контуру L:
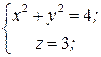 ,
, 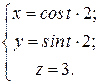
Решение:
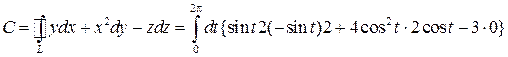 =
=
= - 4 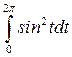 +8
+8 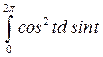 =
= 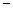 4
4 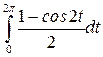 +8
+8 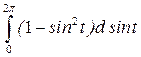 =
=
= 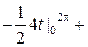
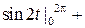
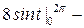
 ;
;
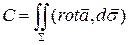 =
= 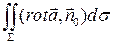 =
= 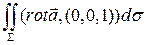 =
= 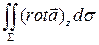 =
=
= 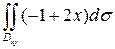 =…
=…
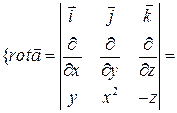
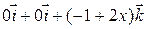 } =
} = 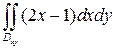 = =
= = 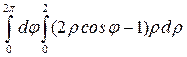 =
=  =
= 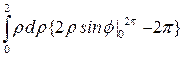 =
=
= 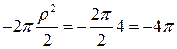 .
.
Инвариантное определение ротора
Ранее было дано определение ротора 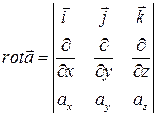 , справедливое лишь в декартовой системе координат.
, справедливое лишь в декартовой системе координат.
Теорема Стокса позволяет дать инвариантное (независящее от системы координат) определение ротора векторного поля.
 Пусть
Пусть 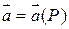 - векторное поле, удовлетворяющее теореме Стокса;
- векторное поле, удовлетворяющее теореме Стокса; 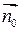 - некоторое фиксированное направление, проходящее через точку М;
- некоторое фиксированное направление, проходящее через точку М;
D - плоская область величины 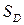 , охватывающая точку М, а L - граница области D. Направления обхода контура L и ориентация области D согласованы в соответствии с теоремой Стокса:
, охватывающая точку М, а L - граница области D. Направления обхода контура L и ориентация области D согласованы в соответствии с теоремой Стокса:
 =
= 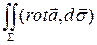 или
или 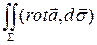 =
= 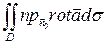 .
.
По теореме о среднем 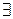 М 1:
М 1: 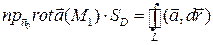 .
.
Тогда 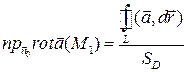 . Будем стягивать контур L в точку М, тогда точка M 1 → M и
. Будем стягивать контур L в точку М, тогда точка M 1 → M и 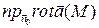 =
= 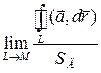 . Поскольку
. Поскольку 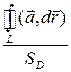 - средняя поверхностная плотность циркуляции поля по площади SD , то проекция
- средняя поверхностная плотность циркуляции поля по площади SD , то проекция 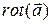 на правление
на правление 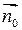 не зависит от выбора систем координат и равна поверхностной плотности циркуляции вектора
не зависит от выбора систем координат и равна поверхностной плотности циркуляции вектора 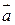 по контуру L, который стягивает площадку, перпендикулярную этому направлению.
по контуру L, который стягивает площадку, перпендикулярную этому направлению.
Дата публикования: 2014-11-04; Прочитано: 775 | Нарушение авторского права страницы | Мы поможем в написании вашей работы!
