Способы преобразования чертежа

Целью преобразования чертежа является проведение заданных на эпюре геометрических элементов в новое положение по отношению к плоскостям проекций, более удобное для решения той или иной задачи.

Преобразование чертежа делают для того, чтобы в новой системе плоскостей проекций геометрические образы (отрезок, плоская фигура и т.п.) проецировались на новую плоскость проекций без искажения, в натуральную величину, либо позволяют получить выразительные проекции отдельных элементов. Построение новых дополнительных проекций называют преобразованием чертежа, что можно осуществить двумя способами:

- выведение дополнительных плоскостей проекций с неизменным положением геометрических элементов;

- перемещение геометрических элементов в пространстве с неизменным положением плоскостей проекций.

Так как частных положений у прямой два и у плоскости два, то существуют четыре исходные задачи для преобразования комплексного чертежа:

- прямую общего положения преобразовать в прямую уровня;

- прямую уровня перевести в проецирующее положение;

- плоскость общего положения преобразовать в проецирующее;

проецирующую плоскость перевести в положение плоскости уровня.

В данной работе рассматриваются только три способа преобразования ортогональных проекций, предусмотренные программой: способ перемены плоскостей проекций, вращения и плоскопараллельное перемещение.

7.1 Способ перемены плоскостей проекций

Способ «перемены» заключается в том, что, вводя дополнительные плоскости проекций, они переходят к другой системе плоскостей проекций, при этом геометрические образы в пространстве сохраняют свое положение. Изменяют направления плоскости проекций: при замене обязательно сохраняется взаимная перпендикулярность двух плоскостей проекций.

Пусть задана точка А и система двух взаимно перпендикулярных плоскостей проекций p₁ и p₂ (рисунок 71). Возьмем плоскость p₄ ^ p₁ и спроецируем точку А на эту плоскость; проекцией будет А₄. Получаем две системы плоскостей проекций: основную p₁ и p₂ и дополнительную p₁ и p₄. Положение точки А в пространстве определяем по двум ее проекциям – А₂ и А₁ в основной системе плоскостей и А₁ и А₄ – дополнительной. При переходе от одной системы плоскостей проекций к другой аппликата Z₁ точки А и ее горизонтальная проекция А₁ точки А остаются неизменными (инвариантными) для двух систем.

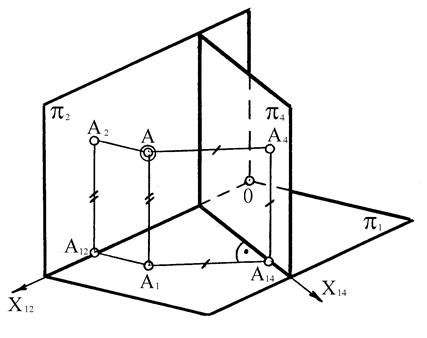
Рисунок 71

Операция перехода от одной системы плоскостей к другой показана на

эпюре (рисунок 72).

Рисунок 72

Для того чтобы по заданной эпюре точки А (А₁, А₂) и новой оси проекций х₁₄

построить проекцию этой точки на плоскость p₄ (А₄), необходимо:

1) из горизонтальной проекции точки А₁ опустить перпендикуляр на новую ось проекций х₁₄;

2) от точки А₁₄ на этом перпендикуляре отложить координату z точки А, т. е. А₁₄ А₄ = А₁₂А₂ = Z_A

Таким образом, если точка в пространстве проецируется на новую плоскость проекций, перпендикулярную к одной из оставленных плоскостей проекций, то расстояние новой проекции точки от новой оси равно расстоянию заменяемой проекции от заменяемой оси.

Заметим, что нельзя менять обе плоскости проекций сразу. Новая плоскость проекций должна сохранять перпендикулярность к остающейся плоскости. Поэтому замену плоскостей можно производить только в последовательном порядке: сначала изменить одну плоскость, затем другую, и, если требуется для решения задачи, эту операцию можно повторять неоднократно. Рассмотрим некоторые примеры.

1. Определение длины отрезка АВ общего положения показано на рисунке 73.

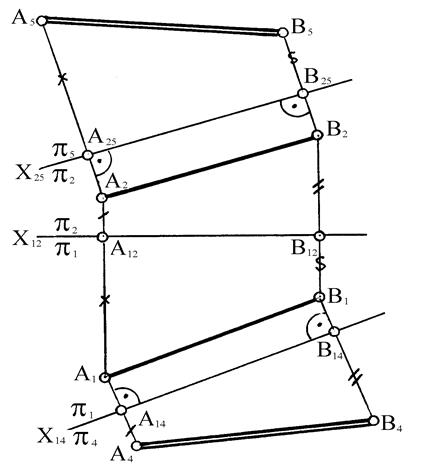
Рисунок 73

Для этого, чтобы данная прямая общего положения АВ оказалась линией уровня, следует ввести новую плоскость p₄ (p₅), которая была бы ей параллельна. На чертеже дополнительная плоскость p₄ параллельна прямой АВ и перпендикулярна к плоскости p₁ (ось Х₁₄ p₁/p₄ параллельна проекции А₁В₁). Через точки А₁ и В₁ проводим новые линии связи, перпендикулярные оси Х₁₄. Расстояние от оси Х₁₄ до А₄ и В₄ равно расстояниям от А₂ и В₂ до оси Х₁₂. Образовавшейся системе плоскостей проекций p₁/p₄ прямая АВ (А₄В₄) является линией уровня, т.е. натуральной величиной отрезка АВ.

Аналогичным построением можно данную прямую АВ преобразовать в горизонталь. Для этого оставим на месте p₂ и заменим p₁ на p₅. Дополнительная плоскость p₅ параллельна прямой АВ и перпендикулярна к плоскости p₂. Теперь прямая А₅В₅ является линией уровня в системе p₂/p₅, т.е. натуральной величиной отрезка АВ.

2. Приведение отрезка прямой общего положения в проецирующую прямую.

На рисунке 74 показан перевод отрезка СД прямой общего положения в положение С₅Д₅ отрезка фронтально-проецирующей прямой.

Рисунок 74

Вначале заменой плоскости p₂ плоскостью p₄ переводим отрезок СД в положение параллельное плоскости p₄, затем, заменив плоскость p₄ плоскостью p₅, поставим отрезок СД по отношению к плоскости p₅ в проецирующее положение, и тогда ее проекция на плоскости p₅ сольется в точку С₅ º D₅, при этом С₄₅С₅ = С₁₄С₂ (или D₄₅D₅ = D₁₄D₂).

3. Чтобы плоскость общего положения преобразовать в проецирующую, необходимо в этой плоскости выбрать одну из главных линий – горизонталь или фронталь, каждая из которых и определяет направление дополнительной плоскости проекций. Если горизонталь плоскости является направлением дополнительной плоскости проекций, то плоскость, перпендикулярная этой плоскости проекций, занимает также относительно ее положение проецирующей плоскости.

Рассмотрим пример преобразования плоскости общего положения a, заданной треугольником АВС, в плоскость проецирующую (рисунок 75).Через вершину А проводим горизонталь. На чертеже горизонтальная проекция А₁1₁ горизонтали А1 определяет направление проекции на дополнительную плоскость проекций. Выбираем дополнительную плоскость проекций p₄ перпендикулярно горизонтали А1 плоскости АВС (p₄ ^ p₁, p₄ ^ АВС, Х₁₄ ^ h ₁) и соответственно перпендикулярно плоскости p₁, и с помощью точек А и С построена проекция плоскости - А₄В₄С₄ – прямая.

Рисунок 75

Очевидно, в образовавшейся системе плоскостей проекций p₁/p₄ плоскость АВС является проецирующей. Заметим, что горизонталь проецируется на плоскости p₄ в виде точки.

4. Определить истинную величину фигуры. Если заданные на чертеже плоские фигуры – плоскости общего положения, для определения их истинной величины недостаточно замены одной плоскости. Новая плоскость проекций должна быть параллельна данной фигуре. В таких случаях необходимо заменить плоскости проекций дважды. Основной принцип замены плоскостей проекций и правила построения проекций точек при этом остаются прежними.

Например, необходимо определить истинную величину треугольника АВС, являющегося плоскостью общего положения (рисунок76).

Рисунок 76

Задача решается двумя последовательными заменами плоскостей проекций. Заменой фронтальной плоскости проекций (p₂) некоторой дополнительной плоскостью проекций (p₄) в образовавшейся системе p₁/p₄

(p₄ ^ p₁, p₄ ^ АВС и Х₁₄ ^ h ₁) плоскость АВС (А₄В₄С₄) будет проецирующей. Затем вводится дополнительная плоскость p₅ (p₅ ^ p₄, p₄ | | АВС,

Х₄₅ | | А₄В₄С₄). Спроецировав треугольник АВС на плоскость p₅, мы получим, очевидно, его истинную фигуру (А₅В₅С₅).

7.2 Преобразование проекций способом вращения

Сущность способа заключается в том, что при неизменном положении основных плоскостей проекций изменяется положение заданных геометрических элементов относительно плоскостей проекций путем их вращения вокруг некоторой оси до тех пор, пока эти элементы не займут частное положение в исходной системе плоскостей проекций. В качестве осей вращения удобнее всего выбрать проецирующие прямые или прямые уровня, тогда точки будут вращаться в плоскостях, параллельных или перпендикулярных плоскостям проекций.

Данный способ широко используется в технике при рассмотрении и исследовании различных вращающихся форм конструкций механизмов и машин.

7.2.1 Вращение вокруг проецирующих прямых линий

Вращением предмета можно построить множество чертежей данного предмета в одной системе плоскостей проекций. При этом основные плоскости проекций остаются неизменными.

Рассмотрим на комплексном чертеже вращение точки вокруг оси, перпендикулярной плоскости проекций. Пусть точка А (рисунок 77) вращается вокруг горизонтально проецирующей прямой j (j^ p₁). Траекторией движения точки А является окружность с центром О на оси вращения в плоскости S, перпендикулярной к оси вращения. Эта плоскость (S) параллельна горизонтальной плоскости проекций, поэтому радиус вращения R = О₁А₁ точки А проецируется на p₁ без искажения, ее горизонтальная проекция А₁ перемещается по окружности (с центром в точке О₁) радиусом ОА. Фронтальная проекция точки А₂ при этом перемещается по прямой, параллельной оси Х.

В качестве примера рассмотрим, как осуществляется перемещение отрезка общего положения в частное положение путем вращения вокруг оси, перпендикулярной плоскости проекций.

Преобразование прямой линии общего положения в линию уровня можно осуществить вращением вокруг оси, перпендикулярной как к плоскости

Рисунок 77

p₁, так и к плоскости p₂. На рисунке 78, а отрезок прямой АВ преобразован вращением во фронтальный отрезок A₂’B₂’.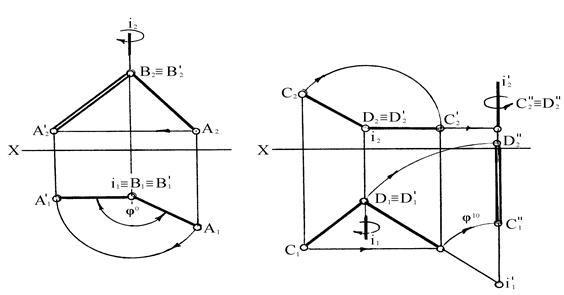

а) б)

Рисунок 78

Ось вращения i ^ p₁ и проходит через точку В. Чтобы осуществить такое перемещение, достаточно повернуть АВ вокруг оси i ^ p₁ на угол j^o так, чтобы после поворота A₁’B₁’ занял положение параллельное оси Х. Так как точка В принадлежит оси вращения i, то она не будет менять своего положения в процессе преобразования. В₁ º В, следовательно, В₁’ º В₁ и В₂ º В₂’. Для нахождения фронтальной проекции точки А₂’ необходимо из А₁’ восстановить перпендикуляр к оси Х и отметить точку его пересечения с горизонтальной прямой, проведенной из точки А₂. Отрезок A₂’B₂’ будет натуральной величиной отрезка АВ.

Преобразование прямой общего положения в проецирующую прямую путем вращения вокруг одной проецирующей оси невозможно. Но зато в проецирующую можно сразу преобразовать прямую уровня. Чтобы преобразовать прямую линию общего положения в проецирующую, требуется произвести последовательно два вращения: первое, преобразуем данную прямую в линию уровня, второе, преобразуем полученную прямую уровня в проецирующую прямую. На рисунке 78, б отрезок СД прямой общего положения переведен в положение, перпендикулярное плоскости p₂.

Отрезок СД вначале вращением вокруг оси i ^ p₁ переведем в положение, параллельное горизонтальной плоскости проекций (С₂’Д₂’ | | X), затем вращением вокруг i’^ П₁, C₁’Д₁’ переместим во фронтально-проецирующее положение C₁’’Д₁’’ ^ Х..

Для того чтобы повернуть плоскость на определенный угол в заданном направлении, необходимо повернуть три любые точки плоскости вокруг одной и той же оси, на один и тот же угол в заданном направлении.

Рассмотрим на примере.

Определить натуральную величину плоскости общего положения a(АВС). Известно, что плоская фигура проецируется в натуральную величину, если она параллельна плоскости проекций. Если плоскость a(АВС) общего положения, то одним поворотом задачу решить невозможно, т.е. необходимо провести два последовательных вращения: первое – повернуть до положения проецирующей плоскости, второе – до положения плоскости уровня. На рисунке 79 в плоскости a(АВС) проведена горизонталь h (h ₁ Ù h ₂). Ось вращения i ^ p₁ Ù С₁ É i₁.

Поворачиваем плоскость a(АВС) до положения перпендикулярности горизонтали к плоскости p₂ (h ₁’ ^ p ₂), горизонтальная проекция плоскости сохраняет свой вид и величину (А₁В₁С₁ = А₁’В₁’С₁’), изменяется лишь ее положение. Так как точки А, В, С при таком повороте перемещаются в плоскостях, параллельных плоскости p₁, то проекции А₂’, В₂’ находятся на горизонтальных линиях связи А₂А₂’ и B₂B₂’. В результате плоскость a(АВС) становится фронтально-проецирующей плоскостью и точки А₂’, В₂’ и С₂ лежат на одной прямой.

При втором повороте, приводящем плоскость a(АВС) в параллельное плоскости p₁ положение, подразумевается ось вращения, перпендикулярная к плоскости p₂ (i’^ p₂, В₂’ É i₂’). Поворачиваем проекцию А₂’, С₂’ до положения параллельного плоскости p₂. Теперь фронтальная проекция при повороте сохраняет свой вид и величину, полученные во второй стадии поворота,

Рисунок 79

точки А₁’, C₁ перемещаются в плоскостях, параллельных плоскости p₂, проекции C₁’’ и A₁’’ находятся на горизонтальных линиях связи с точками C₁’A₁’. Построив проекцию A₁’’B₁’C₁’’, получаем натуральную величину плоскости a(АВС).

7.2.2 Вращение вокруг линий уровня

Вращение плоскости можно осуществить, принимая за ось вращения одну из ее горизонталей или фронталей. Около этой оси будут вращаться все точки, принадлежащие плоскости. Каждая точка опишет в пространстве окружность, плоскость которой будет перпендикулярной к оси вращения. При этом, если точка будет вращаться около горизонтали, то окружность проецируется на плоскость p₁ в виде прямой, перпендикулярной к горизонтальной проекции горизонтали. В случае вращения точки около фронтали окружность вращения проецируется на плоскость p₂ в виде прямой, перпендикулярной к фронтальной проекции фронтали.

Рассмотрим на примере, определить величину угла ВАС (рисунок 80).

Рисунок 80

Здесь для определения величины угла применен поворот вокруг горизонтали: плоскость угла расположится параллельно плоскости p₁. Плоскость однозначно определяется также тремя точками 1, А и С, так как точки С и 1 принадлежат горизонтали, которая принята за ось вращения, то они не меняют своего положения в процессе преобразования. Поэтому, чтобы задать новое положение плоскости (ВАС) | | p₁, достаточно осуществить поворот только одной точки А.

Построения выполнены в следующей последовательности:

а) через точку С проводим горизонталь h (C1), h ₂(C₂1₂) и h ₁(C₁1₁);

б) проведена плоскость вращения точки А – горизонтально проецирующая плоскость d, перпендикулярная к горизонтали (т.е. к оси вращения);

в) определяем центр вращения (О₁, О₂) точки А в пересечении горизонтали с плоскостью d;

г) определяем величину радиуса вращения как гипотенузу прямоугольного треугольника О₁ A₁А₁’, у которого катет А₁А₁’= |Z(.)A-Z(.)O|;

д) из центра О₁ проведена дуга окружности радиуса О₁А₁’, точка пересечения которой с прямой О₁А₁ укажет положение А₁’’- горизонтальная проекция вершины угла после его поворота вокруг горизонтали, и построен угол 1₁А₁’’C₁, равный искомому.

Рассмотрим графические построения для определения натуральной величины треугольника АВС вращением его вокруг горизонтали (рисунок 81), проходящей через вершину С треугольника.

Вершины А и В треугольника вращаются вокруг оси h по окружностям; вершина С принадлежит оси вращения и не изменяет своего положения. Центром вращения точки В является точка О пересечения горизонтали h (оси вращения) с горизонтально проецирующей плоскостью d точки В, перпендикулярной этой оси. Теперь необходимо определить натуральную величину радиуса вращения точки В – отрезок ОВ можно определить построением прямоугольного треугольника – О₁В₁В₁’, гипотенуза его равна радиусу вращения точки В, от центра О вращения точки В по направлению следа d, плоскости ее движения откладываем длину радиуса вращения и отмечаем проекцию В₁’’ точки В, смещенной до плоскости уровня. Другая точка проходит через найденную точку В₁’’ и точку 1₁ из условия, что точка А принадлежит прямой В1 и плоскости d движения этой точки. Проекция А₁’B₁’’C₁ конгруэнтна треугольнику АВС, так как после поворота плоскость треугольника стала параллельной плоскости p₁. Фронтальная же проекция треугольника совпадет с фронтальной проекцией горизонтали, т. е. представляет собой прямую линию (на чертеже она не показана).

Если требуется повернуть плоскую фигуру до положения, параллельного плоскости p₂ , за ось вращения надо выбрать фронталь (все остальные построения аналогичны).

Рисунок 81

7.3 Плоскопараллельное перемещение

Под плоскопараллельным перемещением понимают такое преобразование фигур, когда все их точки, не меняя взаимного расположения, изменяют его относительно неподвижных плоскостей проекций. При плоскопараллельном перемещении все точки фигуры перемещаются в параллельных плоскостях. Обычно это плоскости уровня или проецирующие плоскости. Линии, по которым перемещаются точки, называются их траекториями, это плоские кривые.

При плоскопараллельном перемещении геометрического образа одна из его проекций, оставаясь равной самой себе, перемещается в плоскости проекций, другие проекции точек геометрического образа перемещаются по прямым, параллельным направлению оси проекций. На рисунке 82 показано применение способа плоскопараллельного перемещения к определению натуральной величины треугольника АВС произвольного положения.

Рисунок 82

Такая задача решается двумя последовательными перемещениями. Первым перемещением треугольника АВС переводится в положение, перпендикулярное горизонтальной плоскости проекций. Для этого намечаем в плоскости треугольника фронталь f (C1). Проекцию f₂ (C₂1₂) перемещаем в положение C₂’1₂’ так, чтобы она совпала с направлением проецирования. В этом случае фронталь плоскости АВС перпендикулярна горизонтальной плоскости проекций, а треугольник АВС представляется в горизонтально проецирующей плоскости. Горизонтальная проекция A₁’B₁’C₁’ треугольника проецируется в отрезок прямой.

Вторым перемещением треугольник располагают параллельно фронтальной плоскости проекций. В этом случае горизонтальная проекция A₁’B₁’C₁’ приводится в положение A₁’’B₁’’C₁’’, параллельное направлению оси проекций, а фронтальная проекция A₂’’B₂’’C₂’’ представляет собой треугольник АВС в натуральную величину.

Из рассмотренного примера следует, что плоскопараллельное перемещение можно рассматривать как вращательное без указания осей, т.е. вращательное перемещение вокруг не выявленных проецирующих прямых.

При параллельном перемещении геометрического образа одна из его проекций, оставаясь равной самой себе, перемещается в плоскости чертежа,

другие проекции точек геометрического образа перемещаются по прямым, параллельным направлению оси проекций.

Вопросы для самопроверки

1. Перечислите способы преобразования чертежей геометрических образов.

2.Зачем необходимо преобразование комплексного чертежа?

3. В чем заключается основное различие способов преобразования чертежа?

4. В чем сущность способа замены плоскостей проекций?

5. Как надо расположить новые плоскости проекций, чтобы отрезок прямой общего положения проецировался в натуральную величину, в точку?

6. Как нужно расположить новую плоскость проекции, чтобы плоскость общего положения стала проецирующей?

7. При каком расположении плоской фигуры можно определить ее истинную величину путем замены только одной плоскости проекций?

8. В чем заключается способ вращения?

9. Какие линии используются в качестве линий вращения?

10. Как изменяется фронтальная проекция предмета при вращении его вокруг фронтально проецирующей прямой?

11. Что такое радиус вращения точки?

12. Какую прямую линию принимают за ось вращения при переводе отсека плоскости из общего положения в горизонтально проецирующую плоскость?

13. Какое название встречается для вращения без изображения оси?

14. Укажите последовательность приемов определения натуральной величины отсека плоскости способом плоскопараллельного перемещения?

8 Метрические задачи

Метрическими принято считать задачи, решение которых связано с определением на комплексном чертеже истинных величин расстояний, углов и плоских фигур. В большинстве метрических задач участвуют прямые и плоскости. Следовательно, если заранее будет известно, какие построения необходимо выполнить, чтобы прямая или плоскость общего положения заняла частное положение, то это значительно облегчит решение метрических задач.

Все многообразие метрических задач можно свести к следующим группам:

- задачи на определение расстояния между двумя точками;

- задачи на нахождение величины угла между двумя пересекающимися прямыми;

- задачи на определение истинной величины плоской фигуры.

Первая группа задач включает в себя определение расстояний от точки до другой точки, до прямой, до плоскости, до поверхности; от прямой до другой прямой, плоскости; от плоскости до плоскости.

Вторая группа задач включает в себя определение углов между пересекающимися или скрещивающимися прямыми, между прямой и плоскостью, между плоскостями (определение величины двугранного угла).

Алгоритм решения всех метрических задач опирается на два инварианта ортогонального проецирования:

а) теорему (прямую и обратную) о проецировании прямого угла. Напомним ее: если одна сторона прямого угла параллельна плоскости проекций, то при ортогональном проецировании прямой угол проецируется на эту плоскость в прямой угол (АВС = 90^o) Ù ([ВС) // p₁, ([ВА ^ p₁) Þ А¢В¢С¢// 90^o;

б) свойство любой плоской фигуры проецироваться без искажения, в конгруэнтную фигуру, на ту плоскость проекций, которая параллельна этой фигуре, т. е. (Ф Ì b) Ù (b // p¢) Þ Ф¢ @ Ф.

Рассмотрим решение искомых из перечисленных задач.

8.1 Определение расстояний

Задачи на определение расстояний между геометрическими образами в конечном счете сводятся к нахождению расстояния между двумя точками. При решении метрических задач широко используют преобразования исходного чертежа.

При этом под преобразованием чертежа понимают построения на чертеже, отображающие изменения положения геометрических образов или плоскостей проекций в пространстве и приводящие к образованию нового поля проекций.

1. Расстояние от точки до точки определяется длиной отрезка прямой, соединяющей эти точки. Отрезок прямой линии проецируется в натуральную величину на параллельную ему плоскость проекций. Натуральная величина отрезка может быть получена различными способами:

- способом прямоугольного треугольника;

- способом вращения;

- способом перемены (замены) плоскостей проекций.

На рисунке 83 приведены примеры определения натуральной величины

а) б) в)

Рисунок 83

отрезка ½АВ½ способом проецирования его на дополнительную плоскость проекций, параллельную отрезку½АВ½. На рисунке 83, а использован способ прямоугольного треугольника, когда дополнительная плоскость p¢ É ½ АВ½ и недостающая координата одного конца отрезка – точки А или В равна нулю. На рисунке 83, б – способом вращения отрезка ½АВ½ вокруг проецирующей прямой – оси i или j: i É А, i ^ p₁ или j É А, i ^ p₂. На рисунке 83, в использован способ перемены плоскостей проекций: p₄ // ½АВ½, p₄^ p₁ или p₅ // ½АВ½, p₅ ^ p₂.

2. Расстояние от точки до прямой измеряется отрезком перпендикуляра, проведенного из точки к данной прямой. Отрезок этого перпендикуляра изображается в натуральную величину на плоскости в том случае, если он проведен к проецирующей прямой. Значит, нужно преобразовать чертеж данной прямой, сделав его в новой системе плоскостей проекций, проецирующей. На рисунке 84 определено расстояние от точки С до прямой АВ:

а) p₂ ^ p₁ ® p₁ ^ p₄; p₄ || AB; X₁₄ || A₁B₁;

б) p₁ ^ p₄ ® p ₄ ^ p₅; p₅ ^ АВ; Х₄₅ || A₄B₄;

в) С₅К₅ – истинное расстояние от точки С до прямой АВ.

Рисунок 84

Чтобы построить проекции перпендикуляра СК в исходной системе плоскостей, строим основание перпендикуляра – точку К на прямой АВ из условия, что в системе p₄ ^ p₅ он занимает положение уровня, т.е.

С₄К₄ ^ А₄В₄. Горизонтальная и фронтальная проекция точки К определяется по линиям связи из условия принадлежности ее прямой АВ.

3.Расстояние между двумя параллельными прямыми измеряется отрезком перпендикуляра между ними. На рисунке 85 определено расстояние между прямыми АВ и СД путем преобразования чертежа прямых.

Рисунок 85

Сначала построено изображение прямых линий на плоскости p₄ ^ p₁. В этой системе плоскостей прямые линии занимают положение линий уровня:

АВ (СД) || p₄; Х₁₄ || А₁В₁(С₁Д₁).

В системе плоскостей p₄ ^ p₅ прямые линии занимают проецирующее положение по отношению к плоскости П₅:

p₅ ^ АВ(СД);

Х_{4 5} ^ А₄В₄(С₄Д₄).

Отрезок М₅К₅ между вырожденными проекциями прямых определяет истинную величину расстояния между прямыми АВ и СД.

4. Для определения расстояния между скрещивающимися прямыми линиями необходимо одну из прямых сделать проецирующей в новой системе плоскостей проекций. На рисунке 86 приведено решение задачи на определение расстояния между скрещивающимися прямыми АВ и СД. Решение выполняется в следующей последовательности:

а) p₂ ^ p₁ ® p₁ ^ p₄; p₄ || AB; Х₁₄ || А₁В₁;

б) p₁^p₄ ® p₄ ^ p₅; p₅ ^АВ; Х₄₅ || А₄В₄;

в) М₅К₅ – кратчайшее расстояние между скрещивающимися прямыми.

Рисунок 86

5. Расстояние от точки до плоскости измеряется отрезком перпендикуляра, опущенного из точки на плоскость. Так как перпендикуляр к проеци-

рующей плоскости есть линия уровня, то удобно иметь на чертеже «вырожденную» проекцию данной плоскости. На рисунке 87 построены проекции перпендикуляра ДК, отрезок которого определяет расстояние от точки Д до плоскости a(АВС): p₁ ^ p₂ ® p₁ ^ p₄; p₄ ^ a; Х₁₄ ^ h ₁; h (А,1) Î a.

а) Д₄К₄ ^ a₄ – истинная величина расстояния от точки Д до плоскости a (АВС);

б) К₂ построена с помощью высоты точки К, измеренной на плоскости p₄.

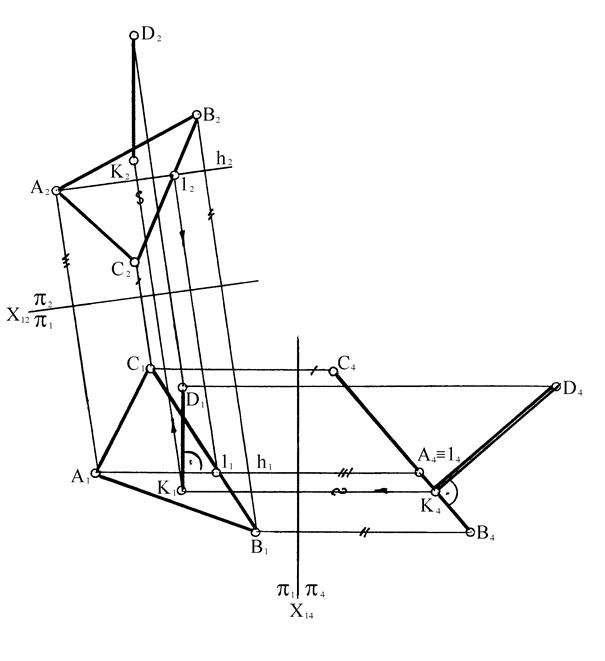
Рисунок 87

6. Расстояние между прямой и параллельной ей плоскостью измеряется отрезком перпендикуляра, опущенного из любой точки прямой на плоскость. Значит, достаточно плоскость общего положения преобразовать в положение проецирующей плоскости, взять на прямой линии точку, и решение задачи будет сведено к определению расстояния от точки до плоскости.

7. Расстояние между параллельными плоскостями измеряется отрезком перпендикуляра между ними, который легко строится, если плоскости займут проецирующее положение в новой системе плоскостей проекций.

На рисунке 88 показано определение расстояния между параллельными плоскостями (a (АВС) // b (f Ç h)) способом замены плоскостей проекций. Для этого выбирается новая плоскость проекций p₄ ^ a Ù b (х₁₄ ^ h₁ и х₁₄ ^ h_оb). На плоскость p₄ заданные плоскости проецируются в прямые. Искомое расстояние – l.

Рисунок 88

8.2 Определение углов

Следующая группа задач включает в себя определение углов между пе-

ресекающимися и скрещивающимися прямыми линиями, между прямой и плоскостью, между плоскостями (определение величины двугранного угла).

1. Для определения величины угла наклона прямой к одной из плоскостей проекций следует заменить вторую плоскость проекций, расположив новую плоскость параллельно прямой; на этой плоскости угол проецируется в натуральную величину. Если прямая линия параллельна плоскости p₂, то угол между этой прямой и плоскостью p₁ изображается без искажения на фронтальной проекции. Если же прямая линия параллельна плоскости p₁, то образуемый этой прямой угол с плоскостью p₂ изображается без искажения на горизонтальной проекции.

2. Угол между пересекающимися прямыми линиями можно определить одним из следующих способов:

- заключением угла в треугольник; следует пересечь стороны угла произвольной прямой и определить натуральную величину полученного треугольника, откуда определяем натуральную величину заданного угла;

- вращением; необходимо поставить плоскость угла в положение, параллельное какой-либо плоскости проекций;

- переменой (заменой) плоскостей проекций; нужно изменить плоскости проекций так, чтобы одна из них стала параллельной плоскости заданного угла.

Наиболее просто и быстро приводит к этой цели способ вращения около горизонтали или фронтали; необходимо совместить заданный угол с плоскостью параллельной горизонтальной (фронтальной) плоскости проекций, проходящей через произвольную горизонталь (фронталь) плоскости угла.

На рисунке 89 истинная величина угла между двумя пересекающимися прямыми определена способом вращения вокруг горизонтали.

В₂

Рисунок 89

Через точку А (А₁, А₂) проведена горизонталь h (h₁, h₂), принадлежащая плоскости угла АВС и принята за ось вращения i. Вокруг этой оси выполнен поворот треугольника АВ1 до положения, параллельного горизонтальной плоскости проекций p₁ (А₁В₁С₁ // p₁). Точки А и 1 расположены на оси вращения, поэтому в процессе вращения своего положения в пространстве не меняют (А º А¢, 1 º1¢), а точка В описывает окружность, плоскость которой проецируется на p₁ в виде прямой, перпендикулярной проекции оси вращения (В₁В₁¢^ h₁). В новом положении треугольника АВ1 радиус вращения точки В проецируется на p₁ без искажения R= О₁В₁¢. Радиус вращения точки В определен способом построения прямоугольного треугольника В_оВ₁О₁.

После поворота плоскость треугольника заняла положение, параллельное плоскости проекций p₁ (А₁В¢₁С₁ // p₁), и проецируется на эту плоскость без искажения ÐА¢₁В¢1¢₁ = ÐАВ1 = a ^o.

На рисунке 90 показано решение этой задачи способом двукратной замены плоскостей проекций.

Рисунок 90

Сначала плоскость угла АВС преобразуется в проецирующую

АВС ^ p₄ плоскости угла АВС (p₅ // АВС, Х₄₅ // А₄В₄С₄). На эту плоскость проекций (p₅) угол АВС проецируется без искажения ÐА₅В₅С₅ @ ÐАВС = a ^o.

3. Угол между двумя скрещивающимися прямыми называется плоский угол, который образуется между двумя прямыми, проведенными из произвольной точки пространства параллельно данным скрещивающимися прямым. На рисунке 91 показан пример решения по определению угла между двумя скрещивающимися прямыми.

Сначала выбирается произвольная точка N. Затем через эту точку проводятся две прямые a и b, параллельные двум заданным скрещивающимся прямым АВ и СD (а // АВ и d // СD. а ₁// А₁В₁. а ₂ // А₂В₂. b ₁ // С₁D₁. b ₂ // С₂D₂). Угол между пересекающимися прямыми линиями a и b ( точк а N – точка их пересечения) определяется любым известным способом преобразования ортогональных проекций. На рисунке 91 показано определение этого угла способом вращения вокруг фронтали.

Рисунок 91

4.Угол между прямой АВ и плоскостью а называют угол j ^o между этой прямой и ее ортогональной проекцией на эту плоскость (т. е. угол ВАВ¢, рисунок 92). На рисунке прямая АВ составляет с плоскостью П¢ угол j ^o

(ВВ¢ ^ p¢). Из приведенного определения следует, что величину угла j ^o можно определить следующим образом (рисунок 92):

а) на прямой l через точку В (В Ë p') проводим прямую a, перпендикулярную заданной плоскости p';

б) находим точку В': В' = a Ç p';

в) находим точку А': А' = l Ç p';

г) строим отрезок А' В';

д) определяем истинный вид угла ВА' В' = j°.

Данная задача решается проще с помощью угла d°, дополнительного до 90^о угла j°: j° + d° = 90^о, j° = 90^о - d°, сторонами угла d° являются прямые l и a (a ^ p¢).

Рисунок 92

На рисунке 93 дан пример определения угла j°, образованного прямой l и плоскостью a (h Ç f´). Задача решена с помощью угла d°: d° =Ð (l, a);

a ₁ ^ h ₁, a ₂ ^ f ₂). Натуральная величина угла определена совмещением его сторон (l, a) с фронтальной плоскостью d путем вращения их вокруг фронтали f´ (фронталь f´ принадлежит плоскости, которую образуют прямые l и a:

f´= {1; 2}, 1 Ì a, 2 Ì l). После определения угла d° вычисляем угол j°:

j° = 90^о - d°.

Рисунок 93

На рисунке 94 показано определение угла j ^о между прямой l,плоскостью a, заданной следами.

Из произвольной точки N, принадлежащей прямой l, опущен перпендикуляр MN на заданную плоскость a (h Ç f): M₁N₁ ^ h _oa, M₂N₂ ^ f _oa (прямая l перпендикулярна плоскости a, если ее проекции перпендикулярны соответствующим пересекающимся следам плоскости h _oa и f _oa).

Угол d^о между двумя пересекающимися прямыми l и MN определен способом двукратной замены плоскостей проекций. Угол j ^о между прямой l и заданной плоскостью определяется как дополнительный до 90^о угол d^о (d^о + j ^о = 90^о).

Рисунок 94

5. Угол, образованный двумя пересекающимися плоскостями a и b

(рисунок 95), называется двугранным (плоскости a и b - грани этого угла, а линия пересечения этих плоскостей АВ - ребро двугранного угла). Двугранный угол между двумя плоскостями измеряется его линейным углом j ^о, полученным при пересечении двугранного угла плоскостью y, перпендикулярной ребру АВ, а следовательно, и граням плоскости a и b: y ^ АВ, y ^ a, y ^ b, j ^о = L (MN,NF),MN = y Ç a,

NF = y Ç b:

При решении данной задачи значительно проще определять не линейный угол j ^о, а угол g ^о, образованный двумя перпендикулярами СD и СE из произвольной точки пространства С на грани плоскостей a и b заданного двугранного угла.

Рисунок 95

Прямые СD и СE задают плоскость y, перпендикулярную двум плоскостям a и b, и линии их пересечения АВ:

СD ^ a, СD Ì y Þ y ^ a,

СE ^ b, СE Ì y Þ y ^ b,

y ^ a, y ^ b Þ АВ =a Ç b.

Между углами j ^о и g ^о существует зависимость

j ^о + g ^о = 180^о,

так как сумма внутренних углов любого плоского четырехугольника равна 360^о, а два угла четырехугольника С DNE - прямые (ÐС DN = 90^о и

ÐCEN = 90^о).

Таким образом, алгоритм определения линейного угла j ^о, измеряющего заданный двугранный угол между плоскостями a и b, можно представить в следующем виде:

а) из произвольной точки пространства С опустить перпендикуляры на заданные плоскости a и b:

СD ^ a, СE ^ b;

б) определить полученный угол g ^о между этими прямыми:

g ^о = ÐDCE;

в) вычислить искомый линейный угол j ^о как дополняющий угол g ^о до 180^о: j ^о = 180^о - g ^о.

Данной зависимостью j ^о = 180^о - g ^о можно пользоваться, когда дополнительный угол g ^о тупой (g ^о > 90^о). Если же этот угол острый (g ^о < 90^о), то он непосредственно равен искомому линейному углу j ^о.

На рисунке 96 в качестве примера показано определение двугранного угла между пересекающимися плоскостями a (АВ Ç ВС) и b (a // b).

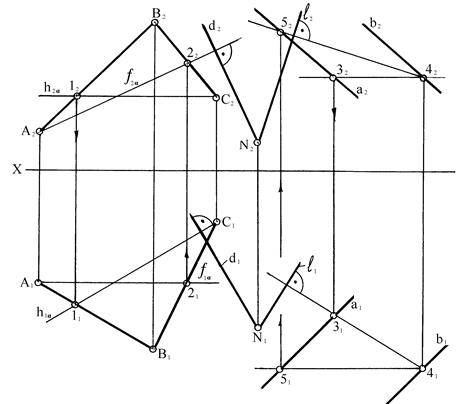
Рисунок 96

Двугранный угол между плоскостями измеряется его линейным углом j ^о. Из произвольной точки пространства N опустим на заданные плоскости перпендикуляры d и l (d ^ a, l ^ b):

d ₁ ^ h _1a, d ₂^ f _2a; l ₁ ^ h _1b, l ₂ ^ f _2b.

Плоский угол между этими перпендикулярами будет равен искомому углу j ^о либо дополняющему его до 180^о.

Определение натуральной величины этого угла (j ^о) может быть определено, например, способом вращения вокруг линии уровня (рисунок 89, например, вокруг горизонтали).

Задача на определение двугранного угла несколько облегчается, если задано ребро этого угла АВ (рисунок 97).

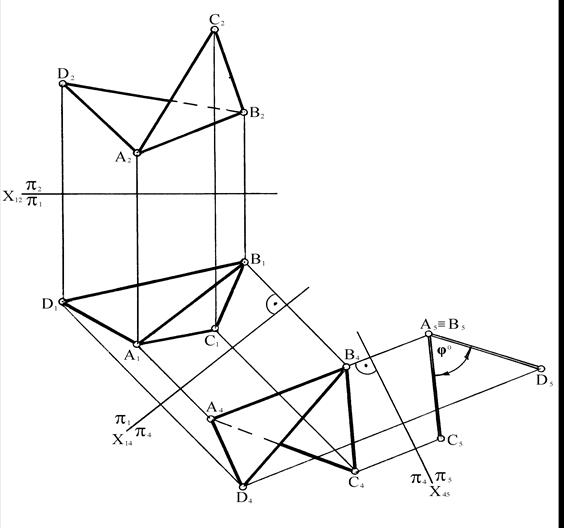
Рисунок 97

Для определения линейного угла j ^о, измеряющего двугранный угол, достаточно расположить его так, чтобы ребро АВ этого угла оказалось перпендикулярным плоскости проекций. Суть решения задачи состоит в том, что проекцию ребра двугранного угла двойной заменой преобразуют в точку, а проекции граней – в две пересекающиеся прямые. Угол между этими прямыми и будет искомым.

Решение задачи на чертеже выглядит следующим образом (рисунок 97). Сначала выбирается плоскость p₄, параллельная ребру АВ (p₄ // АВ, Х₁₄ // А₁В₁), а затем проводится плоскость p₅, перпендикулярная ребру АВ (p₅ // АВ, Х₄₅ ^ А₄В₄).

На новую плоскость проекций p₅ ребро АВ спроецируется в виде точки А₅ º В₅, грани ABD и ABC – отрезками прямых, а линейный угол j ^о – в натуральную величину.

8.3 Натуральная величина плоской фигуры

Следующая группа метрических задач связана с определением истинной величины плоских фигур, произвольно расположенных в пространстве. Такие фигуры проецируются на плоскости проекций с искажениями. Для определения истиной величины плоской фигуры необходимо спроецировать фигуру на параллельную ей плоскость проекций. Данная задача может быть решена различными способами преобразования чертежа: способом замены плоскостей проекций; способом вращения вокруг линии уровня плоскости этой фигуры до совмещения с соответствующей плоскостью уровня; плоскопараллельным перемещением; совмещением. Определив величины этих плоских фигур по их проекциям, можно измерить их линейные и угловые характеристики: длины сторон, углы между сторонами, расстояния от вершин до сторон и т. д.

Ранее достаточно подробно было показано определение величин плоских фигур различными способами, поэтому останавливаться на этом не будем.

Таким образом, мы рассмотрели метрические задачи, связанные с определением, на комплексном чертеже истинных величин расстояний, углов и плоских фигур. Несмотря на то, что чисто метрические задачи встречаются

редко, целесообразно было выделить их в самостоятельную группу. При решении метрических задач, как правило, приходится выяснять вопросы о взаимной принадлежности (или пересечения) геометрических фигур, т.е. решать позиционные задачи.

Вопросы для самопроверки

1. Какие задачи называются метрическими?

2. Какие группы задач выделяют в метрических задачах?

3. Как на комплексном чертеже определить расстояние между двумя точками пространства?

4. Как определить кратчайшее расстояние между двумя параллельными прямыми, скрещивающимися прямыми, от прямой линии до плоскости?

5. В каких случаях угловые величины проецируются без искажения?

6. Как решается задача по определению величины угла между двумя прямыми, прямой и плоскостью, двумя плоскостями?

7. Что является мерой угла между двумя скрещивающимися прямыми?

8. Какие вы знаете способы построения истинной величины фигуры?

Список литературы

1. Гордон В.О., Семенцов – Огиевский М.А. Курс начертательной геометрии: Учебное пособие. – М.: Наука. Гл. ред. Физ.- мат. лит., 1988. – 272 с.

2. Фролов С.А. Начертательная геометрия: Учебник для втузов. – 2-е изд., перераб. и доп. – М.: Машиностроение, 1983. – 240 с., ил.

3. Бубенников А.В. Начертательная геометрия: Учебник для втузов. – 3-е изд., перераб. и доп. – М.: Высш. шк., 1985. – 288 с., ил.

4. Чекмарев А.А. Инженерная графика: Учебн. для немаш. спец. вузов. – М.: Высш.шк.,1985. – 335с., ил.

5. Лагерь А.И., Колесникова Э.А. Инженерная графика: Учеб. для инж.- техн. спец. вузов. – М.: Высш. шк., 1985. – 176 с., ил.

6. Кузнецов Н.С. Начертательная геометрия: Учебник для вузов. – 2-е изд., перераб. и доп. – М.: Высш. школа. 1981. – 262 с., ил.

7. Локтев О.В. Краткий курс начертательной геометрии: Учебник для втузов. – 2-е изд., перераб. и доп. – М.: Высш. шк. 1985. – 136 с., ил.

8. Мукашев М.Ш. Инженерная графика. Часть I. Начертательная геометрия. Лекции и методические указания к выполнению самостоятельных работ.- Алматы, 1999. – 91 с.

Эркин Алимджанович Яхъяев

Техническое черчение

(для учащихся колледжа)

Учебное пособие

Редактор Ж.М. Сыздыкова.

Св. тем. План 2004 г., поз. 15

Сдано в набор ……….2005

Формат 60х84 1/16

Бумага типографская №1

Уч.-изд. лист. 6,5 Тираж 100 экз. Заказ Цена 208 тенге

Подписано в печать …………2005 г.

Копировально-множительное бюро

Алматинского института энергетики и связи,

050013, Алматы, ул. Байтурсынова, 126