 |
Главная Случайная страница Контакты | Мы поможем в написании вашей работы! | |
Логарифмическое дифференцирование
|
|
Показательно-степенной функцией называется функция вида 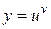 , где
, где  ,
, 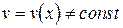 – дифференцируемые функции и
– дифференцируемые функции и 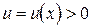 .
.
Для нахождения производной такой функции ее сначала логарифмируют, а затем дифференцируют полученное равенство.
Логарифмическое дифференцирование применяется также для функций, состоящих из большого числа сомножителей или являющихся отношением произведений нескольких функций.
Примеры.
1. Найти производную функции  .
.
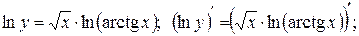
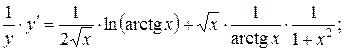
 .
.
2. Найти производную функции 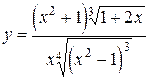 .
.
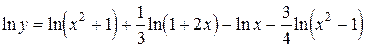 ;
;
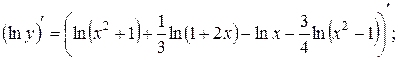
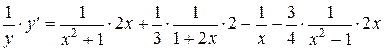 ;
;
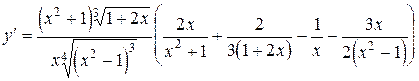 .
.
Замечание. При решении применялись следующие свойства логарифмов:
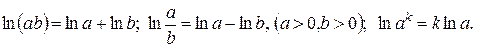
Дифференциал
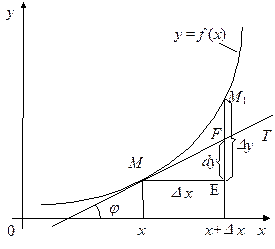
|
К графику непрерывной функции 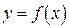 в точке
в точке 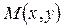 проведем касательную MT, обозначив через j ее угол наклона к положительному направлению оси Ох. Так как
проведем касательную MT, обозначив через j ее угол наклона к положительному направлению оси Ох. Так как 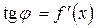 , то из треугольника MEF следует, что
, то из треугольника MEF следует, что 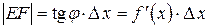 .
.
Введем обозначение  .
.
Это выражение называется дифференциалом функции 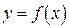 . Итак
. Итак 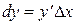 .
.
Замечая, что 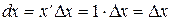 , т.е. что дифференциал независимой переменной равен ее приращению, получим
, т.е. что дифференциал независимой переменной равен ее приращению, получим
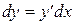 .
.
Таким образом, дифференциал функции равен произведению ее производной на дифференциал (или приращение) независимой переменной.
Из последней формулы следует, что 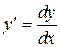 , т.е. производная функции равна отношению дифференциала этой функции к дифференциалу аргумента.
, т.е. производная функции равна отношению дифференциала этой функции к дифференциалу аргумента.
Дифференциал функции dy геометрически представляет собой приращение ординаты касательной, соответствующее приращению аргумента D х.
Из рисунка видно, что при достаточно малом D х по абсолютной величине можно взять приращение функции 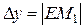 приближенно равным ее дифференциалу, т.е.
приближенно равным ее дифференциалу, т.е.
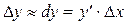 .
.
Все правила дифференцирования можно записать для дифференциалов.
Пусть 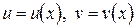 – дифференцируемы в точке х. Тогда
– дифференцируемы в точке х. Тогда
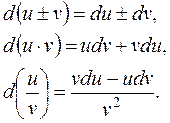
Дата публикования: 2015-11-01; Прочитано: 301 | Нарушение авторского права страницы | Мы поможем в написании вашей работы!
