П. 4. Математическое ожидание

1. Матожидание. Обычно редукция к распределению случайной величины все равно недостаточна: множество значений случайной величины { a 1, a 2, …} бывает слишком большим (и даже бесконечным!), чтобы определить из опыта соответствующие им вероятности p_i.

Опишем распределение одним экспериментальным параметром.

Пусть дана случайная величина x(w). Тогда, если ряд 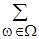x(w) P (w) сходится абсолютно, что означает, что значение его суммы не зависит от порядка слагаемых, то его сумма M x = m = S x(w) P (w) называется математическим ожиданием, или средним значением случайной величины x. Если же сходимость неабсолютная, т.е. условная, то случайная величина не имеет матожидания. Можно доказать, что M x = S aipi.

Примеры.

1. Найти матожидание числа выпавших гербов для 2 монет. См. примеры в §3. Получаем: M x = S aipi = 0´1/4 + 1´2/4 + 2´1/4 = 1.

2. В США вероятность 25-летнему человеку прожить 1 год составляет 0,992. Страховая компания страхует жизнь такого человека на год на сумму Z1000, страховой взнос — Z10. Какую прибыль ожидает получить компания? Величина прибыли есть случайная величина x со значениями Z+10 (если застрахованный не умрет) и Z–990 (если умрет). Имеем распределение 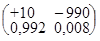, т.е. M x = 10·0,992 – 990·0,008 = 2(Z).

Упр. 4. Найти матожидания: 1) числа выпавших гербов для 3 монет; 2) числа выпавших очков игральной кости.

2. Закон больших чисел. Продуктивно рассматривать не одно событие или случайную величину, а много. Случайные величины возникают в приложениях как результаты измерений, причем либо сами измерения подвержены случайным ошибкам, либо объекты измерения выбираются случайным образом. Тем не менее справедливо правило: даже когда результаты отдельных измерений x1, x2, …, x n сильно колеблются, их средние арифметические (x1 + x2 + … + x n)/ n очень устойчивы.

Пример. В литературе можно найти сведения, что при бросании монеты герб выпадал следующие количества раз: 1) в десяти сериях по 1000 бросаний — 502, 511, 497, 529, 504, 476, 507, 528, 504, 529; 2) в серии 24 000 раз — 12 012; 3) в серии 4040 раз — 2048. Следовательно, частоты выпадений герба группируются около 0,5, хотя и не равны никогда этому числу.

В математике это явление устойчивости средних и отражает закон больших чисел.

Теория графов

Для чего, в самом деле, полюса, параллели,

Зоны, тропики и зодиаки?

И команда в ответ: «В жизни этого нет,

Это — чисто условные знаки».

Льюис Кэрролл. Охота на Снарка.

П. 1. Граф

1. Граф. Два множества: конечное непустое множество V и множество X неупорядоченных пар различных элементов из V,— называются графом.

Вершины графа — элементы множества V, ребра графа — элементы X.

Две вершины графа смежные, если они соединены ребром.

Число вершин называется порядком графа. Граф с p = | V | вершинами и q = | X | ребрами называется (p, q)-графом.

Два графа изоморфны и не различаются, если существует биекция множеств их вершин, сохраняющая смежность вершин.

Примеры.

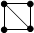1. (4, 5)-граф:

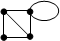2. Не граф: фигура с ребром-петлей:

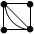3. Не граф: фигура с кратными ребрами:

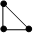
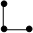
4. Существует всего 4 разных графа порядка 3.

Упр. 1. Нарисуйте все 11 графов порядка 4, упорядочив их по количеству имеющихся ребер.

2. Связный граф. Маршрут —последовательность вершин графа такая, что любые две последовательные вершины смежные, вместе с ребрами, их соединяющими. Цепь — маршрут, у которого все ребра различны.

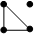Примеры.

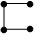
1. Две цепи из трех разных ребер:

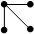2. Три разные ребра, из которых нельзя образовать цепь:

Если в цепи и все вершины различны, кроме, быть может, первой и последней, то это простая цепь. Граф называется связным, если любые две различные его вершины соединены простой цепью.

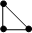
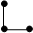Пример. Существуют всего два связных графа порядка 3.

Упр. 2. Нарисуйте все 6 связных графов порядка 4.

3. Подграфом данного графа называется граф, состоящий из вершин и ребер данного графа. " граф разбивается на непересекающиеся связные подграфы — компоненты — следующим образом. Зададим отношение эквивалентности на множестве вершин графа: две вершины эквивалентны, или связаны, если $ простая цепь, их соединяющая. Тогда множество вершин графа распадается на связные классы эквивалентности.

Очевидно, что связный граф состоит из одной компоненты. Граф несвязен, если число его компонент больше 1.

Пример. Единственный 2-компонентный граф порядка 3.

Упр. 3. Нарисуйте все три 2-компонентных графа порядка 4.