П. 2. Отношение эквивалентности

1. Операции на множествах. Объединение, или сумма, множеств A и B называется множество A c B = A + B = {" x: x Î A или x Î B }.

Пересечением, или произведением, множеств A и B называется множество A 1 B = A · B = AB = {" x: x Î A и x Î B }.

Имеют место законы идемпотентности: A c A = A, A 1 A = A.

Разностью множеств B и A называется множество B \ A = B – A = = {" x: x Î B и x Ï A }. Если A Ì B, то разность множеств B \ A называется дополнением множества A до множества B

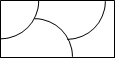
Для изображения операций на множествах используют диаграммы Венна, или Эйлера, которыми пользовался еще Аристотель.

A c B A c B A \ B A \ B

A B A B A B A B

Упр. 3. Нарисуйте на диаграммах Венна: 1) симметрическую разность A Î B = (A\B) c (B\A); 2) множество (A c B)\(B 1 A).

2. Отношение эквивалентности. Любое множество j пар элементов множества A: j = {(a, b): а Î A, b Î A },— называется бинарным отношением на множестве A. Элементы a и b находятся в отношении j, если (a, b) Î j.

Если из того, что (a, b) Î j, следует, что также и (b, a) Î j, то отношение j симметрично, или взаимно.

Если из того, что (a, b) Î j и (b, c) Î j, следует, что (a, c) Î j, то отношение j транзитивно, или переходно.

Если " a Î A (a, a) Î j, то отношение j рефлексивно.

Отношение эквивалентности — бинарное отношение, одновременно симметричное, транзитивное и рефлексивное. Обозначение: ~, a ~ b.

3. Классификация. Разбиение множества A на классы, или классификация — разбиение A на попарно непересекающиеся подмножества, классы, дающие в сумме все A.

Теорема. Если на множестве определено отношение эквивалентности, то тем самым множество разбито на классы эквивалентных элементов. И наоборот, если множество классифицировано, то на нем задано отношение эквивалентности: входящие в один класс элементы эквивалентны.

Примеры.

1. «Быть одного рода» — отношение эквивалентности на множестве существительных русского языка. Докажем это. Симметричность: если слова a и b одного рода, то b и a тоже. Транзитивность: если a и b одного рода, а также b и c одного рода, то a и c того же рода. Рефлексивность: слово всегда того рода, какой имеет. Итак, имеем три класса на множестве существительных: мужской, женский и средний роды.

2. Множество действительных чисел R можно разбить на два класса: алгебраические числа и трансцендентные числа.

U f V f(U)

п. 3. Функция

1. Определение. Пусть U и V — два множества. Функцией, или отображением, из U в V называется такая зависимость, когда для любого x Î U $ единственный y Î V. Здесь x — аргумент функции, или независимая переменная, y — значение функции, или зависимая переменная. Обозначения: f: U ® V; y = f (x).

f		а g		а h		а i		а
		б		б		б		б

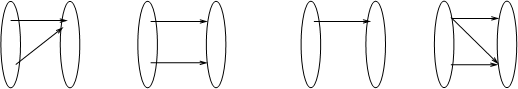Примеры. Пусть U ={1, 2}, V ={а, б}. Зададим следующие зависимости: 1) зависимость f: f (1) = а, f (2) = а; 2) зависимость g: g (1) = а, g (2) = б; 3) зависимость h: h (1) = а; 4) зависимость i: i (1) = а, i (1) = б, i (2) = б.

.

Упр. 4. Какие из зависимостей f, g, h, i — функции, а какие — нет?

2. Биекция. Функция f: U ® V называется сюръек­цией, или отображением «на», если f (U) = V, т.е. образ множества U равен множеству V. Поэтому функция не является сюръекцией, если $ x Î V: x Ï f (U).

Функция f: U ® V называется инъекцией, или вложением, если " x ₁, x ₂ Î U, x ₁ ¹ x ₂ их образы тоже различны: f (x ₁) ¹ f (x ₂). Отсюда функция не является инъекцией, если $ x ₁, x ₂ Î U: x ₁ ¹ x ₂, но f (x ₁) = f (x ₂).

Функция f: U ® V называется биекцией, или взаимно-однозначным cоответствием, если она сюръективна и инъективна одновременно.

Обозначение биекции: f: U «V.

Упр. 5. Какие из примеров f, g, h, i сюръекции, инъекции, биекции?

Нарисуйте иллюстрацию к понятию «биекция».

3. Принцип Дирихле: для любого конечного множества U понятия инъекции, сюръекции и биекции при отображении этого множества на себя f: U ® U совпадают!

Принцип Дирихле формулируют еще так: если в n «ящиках» лежит n + 1 «предмет», то хотя бы в одном «ящике» лежит более 1 «предмета».

Пример. Контрольную работу из 6 вариантов пишут 14 студентов. Докажем, что хотя бы один вариант пишут более двух студентов. Пусть варианты — «ящики», а пары студентов — «предметы». Имеем 6 «ящиков» и 7 «предметов». Тогда по принципу Дирихле хотя бы в одном «ящике» лежит более одного «предмета». Другими словами, хотя бы один вариант пишут более двух студентов.