|
Главная Случайная страница Контакты | Мы поможем в написании вашей работы! | |
Применение метода наименьших квадратов для идентификации в состоянии системы
|
|
Входные и выходные координаты технических систем в процессе их функционирования являются в общем случае нестационарными случайными процессами. Математич. описание нестационарных случайных функций представляет собой достаточно сложную задачу. Поэтому для решения задач обработки измерительной информации естественно попытаться выразить нестационарную случайную функцию через более простые модели случайных сигналов. Простейшей, с практической точки зрения, формой выражения случайной функции является представление ее через комбинацию случайн. величин и известных функций времени:
у (t) = 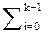 ci ƒi (t), (2.18)
ci ƒi (t), (2.18)
где ci – неизвестные случайные постоянные коэффициенты; ƒi (t) – известные функции времени. Наиболее распространена при инженерных исследованиях полиномиальная аппроксимация, когда в качестве функций ƒi (t) выбираются различные степени аргумента t. В этом случае зависимость (2.18) имеет вид
| у (t) = c 0 + ci t + …+ ck -1 t k -1. | (2.19) |
Для удобства дальнейших выкладок запишем выраж-я (2.19) в дискретном виде и в матричной форме:
| Y Т = X θ Т, | (2.20) |
где Y Т = ║ у 1, …, у i,…, у n║ - вектор наблюдений;
Х = | : : | Δ t (i Δ t) (i Δ t) | … … … | (Δ t)k-1 (i Δ t) k-1 (i Δ t) k-1 | - матрица известных координат; |
θ Т = ║ с 0, …, сi,…, с k -1║ - вектор неизвестных параметров; n – число измерений; k – число неизвестных параметров; T – индекс транспонирования.
Если координаты Y измеряются точно, без случайных ошибок или эти ошибки настолько малы, что ими можно пренебречь, то для определения неизвестных параметров θ достаточно делать ровно столько наблюдений, сколько неизвестных в уравнении (2.20). Тогда единственное решение для неизвестных параметров θ найдется из решения системы линейных уравнений (2.20) в виде θ = Х -1 Y при n = k.
Однако в реальных измерениях Z координаты Y всегда содержаться случайные ошибки, величинами которых пренебрегать нельзя. Поэтому если составить ровно столько независимых уравнений, сколько неизвестных, то ошибки измерений целиком войдут в решение. Для того, чтобы частично компенсировать эти ошибки, принято вводить избыточность, т.е. брать число измерений n и, следовательно, число уравнений (2.20) значительно большим, чем число неизвестных, т.е. n >> k.
Таким образом, с учетом ошибок измерений имеем систему условных уравнений вида:
| Z = Xθ+δ Т, | (2.21) |
где Z Т = ║ z 1 … z i… z n║ - вектор измерений; δ Т = ║ δ1 … δ i… δ n ║ - вектор ошибок; n >> k.
При n > k система уравнений (2.20) несовместна. Однако можно получить единственное решение, оптимальное в некотором смысле. Так, например, существует единственное решение системы уравнений (2.21), обеспечивающее минимум суммы квадратов невязок:
| S 2 = (Z– Xθ) Т (Z– Xθ). | (2.22) |
Получающиеся в результате минимизации функционала (2.22) оценки неизвестных параметров называются оценками наименьших квадратов, а сам метод оценивания – методом наименьших квадратов.
В зависимости от наличия априорной информации о статистических свойствах ошибок измерений метод наименьших квадратов допускает несколько модификаций.
1 Полное отсутствие априорной информации о статистических свойствах ошибок измерений (закон распределения вероятностей ошибок измерений неизвестен, однако предполагается их независимость и нулевое математическое ожидание). В этом случае оценки неизвестных параметров находим дифференцированием выражения (2.22) и приравниванием полученных выражений нулю:
dS 2 / d θ i = 2 (Z – X 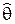 ) Т Х = 0. ) Т Х = 0.
| (2.23) |
В результате получаем систему нормальных уравнений, которая в соответствии с соотношением (2.23) имеет вид
(X Т X) 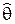 = X Т Y. = X Т Y.
| (2.24) |
Оценка неизвестных параметров 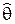 определяют из соотношения (2.24):
определяют из соотношения (2.24):
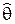 = (X Т X) -1(X Т Z). = (X Т X) -1(X Т Z).
| (2.25) |
Поскольку закон распределения вероятностей ошибок измерений неизвестен, определить закон распределения оценок 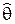 также не представляется возможным. Однако в показано, что полученные в результате приведенной процедуры оценки являются несмещенными эффективными оценками, точность которых можно охарактеризовать дисперсионной матрицей
также не представляется возможным. Однако в показано, что полученные в результате приведенной процедуры оценки являются несмещенными эффективными оценками, точность которых можно охарактеризовать дисперсионной матрицей
| D = (X Т X)-1 σ2. | (2.26) |
Диагональные элементы матрицы (2.26) определяют дисперсии, а недиагональные – ковариации оценок. Сомножитель σ 2 является неизвестным, однако метод наименьших квадратов одновременно с оценкой неизвестных параметров θ позволяет также определить и оценку неизвестной дисперсии σ 2 погрешностей измерений. Такой несмещенной эффективной оценкой дисперсии погрешности измерений является оценка вида:
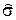 2 = S 2 = S 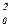 / (n - k), / (n - k),
| (2.27) |
где S 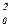 = min (Z – Xθ) Т (Z – Xθ) = (Z – Xθ) Т (Z – Xθ) – остаточная сумма квадратов.
= min (Z – Xθ) Т (Z – Xθ) = (Z – Xθ) Т (Z – Xθ) – остаточная сумма квадратов.
2 Закон распределения ошибок неизвестен (ошибки зависимы, имеют нулевое математическое ожидание и корреляционную матрицу σ 2G, где G – известная матрица, σ 2 – неизвестный сомножитель). В этом случае в качестве критерия оптимальности выбирается взвешенная сумма квадратов:
| S 2 = (Z – Xθ) Т ω (Z – Xθ), | (2.28) |
где ω = G-1.
Оценки наименьших квадратов неизвестных параметров (2.28) определяются так же, как и в системе (2.24), и имеют вид:
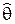 = (X Т ω X) -1(X Т ω Z). = (X Т ω X) -1(X Т ω Z).
| (2.29) |
Точность полученных оценок характеризуется дисперсионной матрицей
| D = (X Т ω X)-1 σ2. | (2.30) |
Неизвестный сомножитель σ2 находится как
σ 2 = ((Z – X 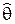 )Т ω (Z – X )Т ω (Z – X 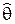 )) / (n - k). )) / (n - k).
| (2.31) |
При прочих равных условиях ковариационная матрица σ2 G= Σ полностью известна. Тогда оценки 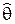 и точность этих оценок определяются по формулам (2.29), (2.30) при выборе в качестве функции ω = Σ-1.
и точность этих оценок определяются по формулам (2.29), (2.30) при выборе в качестве функции ω = Σ-1.
Основные расчетные формулы изложенных модификаций метода наименьших квадратов (МНК) сведены в таблицу.
| Основные соотношения МНК | Основные соотношения при различной априорной информации | ||
| σ 2 | σ 2 G | Σ | |
| Квадратичная форма, подлежащая минимизации | (Z – Xθ) Т (Z – Xθ) | (Z – Xθ) Т G-1(Z –Xθ) | (Z – Xθ) Т (σ 2G)-1(Z – Xθ) |
| Оценка | (X Т X)-1(X Т Z) | (X Т G-1X)-1(X Т G-1Z) | (X Т (σ 2G)-1X)-1(X Т (σ 2G)-1Z) |
| Матрица ковариаций | σ2 (X Т X)-1 | σ2 (X Т G-1X)-1 | (X Т (σ 2G)-1 X)-1 |
Точность оценок методом наименьших квадратов
Оценки наименьших квадратов неизвестных параметров являются точечными оценками, поэтому определение меры отклонения этих оценок от их истинных значений невозможно, если неизвестны вид и параметры распределения ошибок измерения.
Если погрешности измерения распределены по нормальному закону
δ ~ N (0, σ 2, G),
то оценка наименьших квадратов неизвестных параметров θ также описывается нормальным законом распределения:
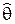 ~ N (θ, D). ~ N (θ, D).
| (2.32) |
Проверка адекватности модели при применении методов наименьших квадратов
Измеряемые координаты технических систем представляют собой в общем случае комбинацию нестационарного полезного сигнала и стационарной помехи. Упрощенная аппроксимация таких процессов полиномами заданного порядка возможна лишь в сравнительно узких интервалах времени, длина которых, как правило, заранее неизвестна и должна определяться на основе тех же измерений, которые используются для оценивания состояния системы. Степень аппроксимирующего полинома также не может быть выбрана априорно, она подбирается путем анализа этих же измерений.
Дата публикования: 2015-11-01; Прочитано: 1016 | Нарушение авторского права страницы | Мы поможем в написании вашей работы!