Постановка задачи распознавания технического состояния оборудования

Техническая диагностика – наука о распознавании состояния технической системы, включающая широкий круг проблем, связанных с получением и оценкой диагностической информации. Техническая диагностика изучает методы получения и оценки диагностикой информации, диагностические модели и алгоритмы принятия решений. Наиболее важным показателем надежности является отсутствие отказов во время работы технической системы. Техническая диагностика, позволяет устранить подобные отказы в процессе технического обслуживания. Основной задачей технической диагностики является распознавание состояния технической системы в условиях ограниченной информации. Теоретическим фундаментом для решения основной задачи технической диагностики следует считать общую теорию распознавания образов. Алгоритмы распознавания в технической диагностике частично основываются на диагностических моделях, устанавливающих связь между состояниями технической системы и их отображениями в пространстве диагностических сигналов. Для принятия обоснованного решения целесообразно привлекать методы теории статических решений. Решение задач технической диагностики связано с прогнозированием надежности до следующего технического осмотра. Здесь решения должны основываться на моделях отказов. Вторым важным направлением технической диагностики является теория контролеспособности. Контролеспособностью называется свойство изделия обеспечивать достоверную оценку его технического состояния и ранее обнаружение неисправностей и отказов. Состояние системы описывается совокупностью (множеством) определяющих ее параметров (признаков). Распознавание состояния системы – отнесение состояния системы к одному из возможных классов (диагнозов). Число диагнозов зависит от особенностей задачи и целей исследования.

Часто требуется провести выбор одного из двух диагнозов (дифференциальная диагностика или дихотомия), например, «исправное состояние» и «неисправное состояние». В других случаях необходимо более подробно охарактеризовать неисправное состояние. В большинстве задач технической диагностики диагнозы (классы) устанавливаются заранее, и в этих условиях задачу распознавания часто называют задачей классификации.

Совокупность последовательных действий в процессе распознавания называется алгоритмом распознавания. Существенной частью процесса распознавания является выбор параметров, описывающих состояние системы. Математическая постановка задачи. В задачах диагностики состояния системы часто описывается с помощью комплекса признаков [4]

K = (k ₁, k ₂, …, k_j, …, k_ν), (2.1)

где k_j – признак, имеющий m_j разрядов.

Каждый разряд (интервал) признака k_j обозначается k_js. Фактически наблюдаемое состояние соответствует определенной реализации признака, что отмечается верхним индексом ^*.

В общем случае каждый экземпляр системы соответствует некоторой реализации комплекса признаков:

K ^* = (k ₁^*, k ₂^*, …, k_j ^*, …, k_ν ^* ). (2.2)

Во многих алгоритмах распознавания удобно характеризовать систему параметрами х_j, образующими ν -мерный вектор или точку в ν- мерном пространстве:

Х = (х ₁, х ₂, …, х_j, …, х_ν ). (2.3)

В большинстве случаев параметры х_j имеют непрерывное распределение.

С помощью признака k_j получается дискретное описание, тогда как параметр х_j дает непрерывное описание. Как указывалось, в задачах технической диагностики возможные состояния системы – диагнозы D_i – считаются известными.

Существуют два основных подхода к задаче распознавания: вероятностный и детерминистский. Постановка задачи при вероятностных методах распознавания такова. Имеется система, которая находится в одном из n случайных состояний D_i. Известна совокупность признаков (параметров), каждый из которых с определенной вероятностью характеризует состояние системы. Требуется построить решающее правило, с помощью которого предъявленная (диагностируемая) совокупность признаков была бы отнесена к одному из возможных состояний (диагнозов).

При детерминистских методах распознавания удобно формулировать задачу на геометрическом языке. Если система характеризуется ν -мерным вектором Х, то любое состояние системы представляет собой точку в ν -мерном пространстве параметров (признаков). Предполагается, что диагноз D_i соответствует некоторой области рассматриваемого пространства признаков. Требуется найти решающее правило, в соответствии с которым предъявленный вектор Х ^* (диагностируемый объект) будет отнесен к определенной области диагноза. Таким образом, задача сводит к разделению пространства признаков на области диагнозов. При детерминистском подходе области диагнозов обычно считаются «непересекающимися», т.е. вероятность одного диагноза (в область которого попадает точка) равна единице, вероятность других равна нулю. Основное преимущество статистических методов распознавания состоит в возможности одновременного учета признаков различной физической природы, так как они характеризуются безмерными величинами – вероятностями их появления при различных состояниях системы.
7 Математические модели в задачах диагностики

Экспериментальные данные, обеспечивающие получение статических зависимостей, описывающих связи между нарушением в конструкции объекта и измеряемым параметром, можно получить только для объектов массового производства. В некоторых случаях такие зависимости получить невозможно. Тогда один из способов получения необходимой информации – использование уравнений, описывающих процессы в элементах объекта, в том числе и процесс развития неисправности, т.е. математических моделей объекта. В результате расчётов с использованием, как уравнений объекта, так и уравнений неисправности, устанавливается связь между степенью развития неисправности и поведением измеряемых параметров, т.е. информация, необходимая для формирования алгоритмов систем функционального диагностирования (СФД).

Математические модели элементов системы диагностики

Математические модели (ММ) элемента системы – это совокупность дифференциальных и алгебраических уравнений, эмпирических формул, таблиц, графиков, описывающих характеристики элемента (агрегата, узла), т.е. связи между внутренними и внешними управляющими и возмущающими параметрами [2]:

F (x, y, u) = 0 (1)

где x – вектор параметров объекта; y – вектор управляющ. воздействий; u – вектор возмущающ. воздействий

Для задач функциональной диагностики ММ применяются при моделировании (численный эксперимент) развития той или иной неисправности с целью выявления диагностических признаков и проверки эффективности работы технических средств диагностики. Существуют ММ нормально функционирующего элемента и ММ, в которые заложены данные развития той или иной неисправности. Последние ММ определяют связи между изменением конструктивных параметров, вызывающих ненормальную работу объекта, и измеряемыми параметрами. Эти два типа ММ могут существенно отличаться, так как появление неисправности может изменить структуру объекта, а также приводит к появлению новой переменной, характеризующей степень развития неисправности.

По способу формиров-я ММ можно разделить на аналитические, эмпирические и полуэмпирические. По форме записи используемых уравнений, а точнее – по глубине описания процесса, все ММ делятся на линейные и нелинейные. Из соотношения между характерной постоянной времени системы и временем развития неисправности выясняется вопрос о необходимости учета динамических процессов в системе или возможности ограничиться использованием статической ММ.

Аналитические модели содержат дифференциальные уравнения, граничные и начальные условия к ним, алгебраические зависимости, полученные из общих физических закономерностей. Преимущество аналитических ММ – их общность, возможность описания процессов в достаточно широком круге объектов. Существенные недостатки этих ММ – невысока точность описания свойств многих объектов из-за сложности реальных процессов и отсутствия для них достаточно точных аналитических зависимостей, а также трудоемкость нахождения решений, описывающих более или менее сложные процессы, даже с использованием современных ЭВМ.

Эмпирические (экспериментальные) модели обладают достаточной точностью, однако для получения функциональных связей между параметрами процесса в объекте и внешними возмущениями или регулирующими параметрами необходим большой объем экспериментов. Результаты экспериментов не всегда можно распространить на подобные объекты. Для получения обобщенных экспериментальных зависимостей, пригодных для описания процессов в ряде однотипных объектов, необходимо использовать методы теории подобия.

Наибольшее распространение получили смешанные полуэмпирические ММ, при формировании которых используются как общие физические закономерности, так и данные экспериментов, которые позволяют учесть многие детали процесса, не учитываемые аналитическими ММ.

В случае формирования чисто эмпирических и полуэмпирических ММ для выбора наиболее удобной формы уравнений и определения их коэффициентов используются методы идентификации

В нелинейных уравнениях, записываемых в форме (1), переменные x, y, u и их производные входят в виде произведений, степеней, трансцендентных функций и т.д. Линейные (линеаризированные) уравнения имеют форму

A (s) x = φ (y, u), (2)

где A (s) – квадратная матрица, коэффициенты которой – многочлены по s; s = d / d t – оператор дифференцирования.

Для линейных уравнений существуют хорошо разработанные методы решения, для них применим принцип суперпозиции; для нелинейных уравнений таких общих методов решений нет. Для большинства объектов изменения параметров процессов в достаточно широком диапазоне описываются нелинейными зависимостями.

В зависимости от класса решаемой задачи один и тот же объект можно описать как нелинейными, так и линейными (линеаризованными) уравнениями, и если позволяют условия использования результатов решения, всегда имеет смысл хотя бы в первом приближении решать линейное (линеаризованное) уравнение.

При построении ММ допустимая степень упрощения модели определяется условиями функционирования системы.

Модели объектов, состоящих из связанных между собой элементов (агрегатов, устройств), формируются в два этапа: вначале создание ММ процессов в отдельных органах, агрегатах, узлах системы, а затем разработка ММ всей системы в целом с участием частных ММ отдельных подсистем и структуры связей между ними. Для анализа состояния системы необходимо из ММ элементов собрать ММ всей системы, однако совокупность всех ММ, входящих в систему элементов, не является еще ММ системы. Для формирования замкнутой системы уравнений к уравнениям элементов необходимо добавить уравнения связей между параметрами входящих в ММ элементов

Модели неисправности

Под моделью неисправности понимается аналитическая или стохастическая зависимость, связывающая параметр, характеризующий степень развития неисправности, с временем или параметрами объекта диагностики. В качестве параметра, характеризующего неисправность, обычно используются первичные конструктивные параметры объекта, изменение которых является причиной появления признаков неисправности – изменения измеряемых параметров.

Как правило, используются ММ простых неисправностей, которые связаны с отклонением от нормального значения конструктивного параметра только одного агрегата объекта диагностики. Случай сложной неисправности, когда от нормального значения отклоняются одновременно (или в какой-то последовательности) конструктивные параметры ряда агрегатов, очень неудобен как для моделирования, так и для диагностики из-за многообразия возможных сочетаний параметров по величине, взаимной последовательности и т.д.

Если моделируются неисправности, нарушающие структуру моделируемой системы, то возможные неисправности должны быть заранее предусмотрены в ММ в виде отдельных структурных элементов.

Для воспроизведения картины развития неисправности с помощью ММ объекта в первую очередь необходимо определить, за какое характерное время развивается неисправность. Если это время соизмеримо или меньше характерной постоянной времени объекта, то необходимо использовать ММ объекта диагностики, в которой учтены динамические эффекты, т.е. члены с производными по времени.

Возможен другой вариант соотношения характерных времен, когда время развития неисправности намного больше постоянной времени объекта. В этом случае можно использовать квазистационарную ММ объекта, в которой отсутствуют члены с производными по времени.

Математические модели теории надежности

В настоящее время системная теория надежности стала составной частью более общего раздела прикладных наук – теории больших систем. На этой основе далее развивают методологию проектирования систем, обладающих высокими показателями надежности.

При постановке большинства задач показатели надежности элементов считают заданными. Технические системы радиоэлектроники, автоматики и вычислительной техники состоят в основном из элементов массового производства и работают в сравнительно однородных условиях. Ресурсные испытания элементов этих систем относительно просты, а условия эксплуатации допускают воспроизведение в лабораторных условиях. Статистическая обработка результатов испытаний позволяет выбрать подходящие аналитические зависимости для изменения показателей во времени и оценить численные значения необходимых параметров. Для невосстанавливаемых элементов обычно ищут подходящие аналитические аппроксимации либо для вероятности безотказной работы Р (t), либо для интенсивности отказов λ (t).

Если интенсивность отказов задана, то решение задачи относительно функции Р (t) при начальном условии Р (0) = 1 записывается в виде

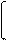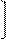t Р (t) = exp - ∫ λ (τ) dτ.

(4)

Если вероятность наступления отказа в начальный момент t = 0 отлична от нуля, то решение записывается в виде

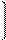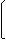t Р (t) = Р (0) exp - ∫ λ (τ) dτ.

(5)

Ресурсные испытания и наблюдения над большими выборками объектов показывают, что в большинстве случаев интенсивность отказов изменяется во времени немонотонно. После начального периода приработки наступает относительно длительный этап, когда интенсивность отказов приблизительно постоянна (рисунок 2.1). Затем вследствие изнашивания, старения, накопления повреждений и других процессов интенсивность отказов возрастает. Когда интенсивность отказов достигает некоторого уровня, дальнейшая эксплуатация нецелесообразна. Если за начало эксплуатации объектов принять момент окончания приработки, а за предельное состояние – начало заметного возрастания интенсивности отказов, то на отрезке эксплуатации можно считать λ = const. В результате вместо (2.8) можно записать

Р (t) = exp (- λ t).	(6)
	λ (t)
	0	Т	t

Формула (6) выражает экспоненциальный закон надежности, который широко применяют в прикладных расчетах. Математическое ожидание срока службы (ресурса) равно 1/ λ. Поэтому формулу (5) можно записать в виде

Р (t) = exp (- t / tс),

(7)

где t_с = Е [ Т ].

Многосторонняя модель поврежденности

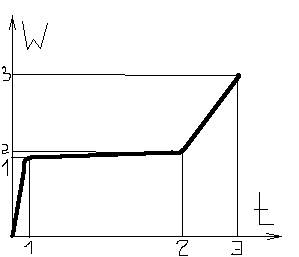Особое место среди нелинейных моделей накопления повреждений занимают многостадийные модели, отражающие тот факт, что многие процессы накопления повреждений состоят из двух или большего числа стадий, каждая из которых протекает по своим законам. Типичная зависимость, состоящая из трех стадий, показана на рисунке. Эту зависимость можно интерпретировать, например, как изменение износа при постоянных нагрузках. Первая, начальная стадия – приработка. При значении t = Т_{b 1} (q) износ достигает значения ψ = ψ ₁, после чего наступает вторая стадия, в течения которой скорость изнашивания приблизительно постоянна. Большинство деталей вырабатывает свой ресурс именно на этой стадии. При t = Т_{b 2} (q) и ψ = ψ ₂ начинается заключительная стадия - интенсивное изнашивание. Предельное состояние наступает при t = Т_{b 3} (q). Для этого состояния ψ = ψ _* = 1. Если за предельное состояние принимают момент окончания стадии установившегося изнашивания, процесс состоит из двух стадий. При этом следует принять ψ ₂ = 1.

Статические методы формирования математических моделей

Описанные выше детерминированные ММ объектов диагностики характеризуют некоторые средние значения (математическое ожидание) параметров системы. В действительности исходные данные, заключенные как в коэффициентах уравнений, так и в начальных и граничных условиях, описывающих внешние условия для объекта, являются случайными величинами или случайными функциями. Для учета случайного характера всех параметров системы, кроме математического ожидания этих параметров, необходимо знать дисперсию (разброс) и закон распределения этих характеристик. Зная дисперсию и законы распределения, можно сформировать статистическую ММ, у которой коэффициенты уравнений, константы, внешние условия будут известными случайными функциями.