 |
Главная Случайная страница Контакты | Мы поможем в написании вашей работы! | |
Операции над матрицами
|
|
Сложение и вычитание матриц сводится к соответствующим операциям над их элементами. Самым главным свойством этих операций является то, что, они определены только для матриц одинакового размера. Таким образом, можно определить операции сложения и вычитания матриц:
Определение. Суммой (разностью) матриц A и B одинаковых размеров m´n является матрица С = А + В того же размера, элементы которой равны сумме соответствующих элементов исходных матриц, т.е.: cij = aij ± bij, i = 1,2, …, m; j = 1,2,…,n.
Определение. Произведением матрицы А на число a называется матрица В = aА, элементы которой bij = a aij, i = 1,2, …, m; j = 1,2,…,n.
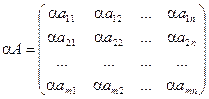
Пример. Даны матрицы А = 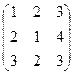 ; B =
; B = 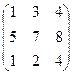 , найти 2А + В.
, найти 2А + В.
Определение: Произведением матриц Аm´k×Bk´n называется такая матрица Сm´n, каждый элемент которой cij равен сумме произведений элементов i-ой строки матрицы А на соответствующие элементы j-го столбца матрицы В: 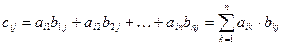 , i = 1,2, …, m; j = 1,2,…,n.
, i = 1,2, …, m; j = 1,2,…,n.
Из приведенного определения видно, что операция умножения матриц определена только для матриц, число столбцов первой из которых равно числу строк второй.
Пример. Вычислить произведение А×В, где
А= 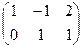 ; В =
; В = 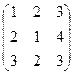 .
.
Многие свойства, присущие операциям над числами, справедливы и для операций над матрицами (это следует из определения этих операций)
Свойства операции над матрицами.
1) А + В = В + А;
2) (А + В) + С = А + (В + С);
3) a(А + В) = aА + aВ;
4) А×(В + С) = А×В + А×С;
5) (А + В)×С = А×С + В×С;
I. a(А ×В) = (aА)В = А(aВ);
7) (АВ)С = А(ВС).
Однако имеются и специфические свойства матриц. Так, операция умножения матриц имеет некоторые отличия от умножения чисел:
I. Если произведение матриц АВ существует, то после перестановки сомножителей произведение матриц ВА может и не существовать. Действительно, в примере, приведенном выше, получили произведение матриц А2´3×B3´3 = С2´3, а произведение В3´3×А2´3 не существует.
II. Если даже произведения АВ и ВА существует, то они могу быть матрицами разных размеров. Например, А2´3×B3´2= С2´2, а В3´2×А2´3= D3´3.
III. Умножение матриц не коммутативно, т.е. АВ ¹ ВА даже если определены оба произведения и обе матрицы одинакового размера (это возможно только при умножении квадратных матриц А и В одинакового порядка).
Пример. Найти произведения АВ и ВА, где
А = 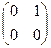 , В =
, В = 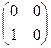 .
.
Однако, если для каких – либо матриц соотношение АВ=ВА выполняется, то такие матрицы называются перестановочными (коммутирующими между собой).
Самым характерным примером может служить единичная матрица, которая является перестановочной с любой квадратной матрицей того же порядка:
А×Е = Е×А = А
Перестановочными могут быть только квадратные матрицы одного и того же порядка.
Очевидно, что для любых матриц выполняются следующее свойство:
A×O = O; O×A = O,
где О – нулевая матрица.
IV. Произведение двух ненулевых матриц может равняться нулевой матрице, т.е. из того, что АВ = 0, не следует, что А=0 или В=0. Например, А= 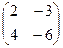 , B=
, B= 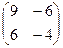 , но АВ =
, но АВ = 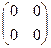 = 0.
= 0.
V. Важным частным случаем произведения матриц является произведение квадратной матрицы Аn´n на вектор-столбец Х = 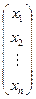 :
:
А× Х =  ×
× 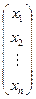 =
= 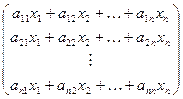 = x1
= x1 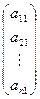 + x2
+ x2 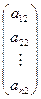 +... + xn
+... + xn 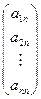 , т.е. вектор А× Х является линейной комбинацией столбцов матрицы А с коэффициентами xi.
, т.е. вектор А× Х является линейной комбинацией столбцов матрицы А с коэффициентами xi.
Аналогично при умножении матрицы А на вектор-строку(слева) Х А мы получаем вектор-строку, являющийся линейной комбинацией строк матрицы А с коэффициентами xi.
Рассмотрим еще одну операцию – транспонирование матрицы
Определение. Транспонирование матрицы – переход от матрицы А к матрице АТ, в которой строки и столбцы поменялись местами с сохранением порядка. Матрица АТ называется транспонированной относительно матрицы А:
А = 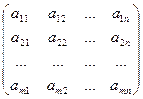 ; АТ=
; АТ= 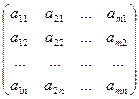 ;
;
Из определения следует, что если матрица А имеет размер m´n, то транспонированная матрица АТ имеет размер n´m.
Свойства операции транспонирования:
1) (АТ)Т = А;
2) (kA)T = kAT;
3) (A + B)T = AT + BT;
4) (АВ)Т = ВТАТ.
Пример. Даны матрицы А = 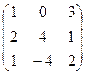 , В =
, В = 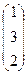 , С =
, С = 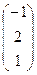 и число a = 2. Найти АТВ+aС.
и число a = 2. Найти АТВ+aС.
Дата публикования: 2015-11-01; Прочитано: 613 | Нарушение авторского права страницы | Мы поможем в написании вашей работы!
