 |
Главная Случайная страница Контакты | Мы поможем в написании вашей работы! | |
Лабораторная работа № 12
|
|
Программирование численных в среде пакета Mathcad
на примере решения уравнения
ЦЕЛЬ. Изучить численные методы решения уравнений, научиться использовать возможности Mathcad для программирования численных методов.
Основные положения
В лабораторной работе № 9 мы с вами уже рассматривали решение уравнений в среде пакетаMathcad – графическим методом, с помощью функции root, с помощью решающего блока Given и функции Find. Сегодня мы рассмотрим решение уравнения с помощью численных методов и найдем решение уравнения, создав программы по описанным ниже методам.
Метод половинного деления (бисекции)
Механизм метода бисекции, который больше известен под названием метода половинного деления, очень прост и заключается в том, что полученный при локализации отрезок на каждой итерации делится пополам. Из двух половинок выбирается та, на концах которой функция принимает значения противоположных знаков. То есть проверяется то же условие, что и при методе сканирования. Процесс заканчивается, когда длина полученного интервала становится меньше произведения 2Ɛ. Фактически этот метод исключает возможность появления ошибки. «Аварийная» ситуация может быть вызвана лишь тем, что граница полученного на итерации отрезка попадет в точку разрыва функции. Метод половинного деления наиболее универсальный среди всех итерационных методов. Но, как всегда, бочка меда не обходится без ложки дегтя – для бисекции характерна очень низкая скорость сходимости.
Итерационная формула метода бисекции:
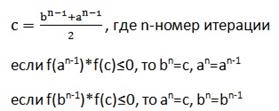
Скорость сходимости: низкая
Надежность сходимости: высокая
Метод Ньютона
Задан отрезок [а,b], содержащий корень уравнения F(x)=0. Уточнение значения корня производится путем использования уравнения касательной. В качестве начального приближения задается тот из концов отрезка [а,b], где значение функции и ее второй производной имеют одинаковые знаки (т.е. выполняется условие F(x0)*F"(x0) > 0).
В точке F(x0) строится касательная к кривой у = F(x) и ищется ее пересечение с осью х. Точка пересечения принимается за новую итерацию. Метод Ньютона самый быстрый способ нахождения корней уравнений
Итерационная формула имеет вид:
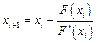
Итерационный процесс проходит до того времени, пока не будет выполнено условие |F(X)|< e, где e - заданная точность.

Рис. 1. Иллюстрация метода Ньютона
Рис. 1. иллюстрирует работу метода Ньютона. В данном случае вторая производная функции положительна, поэтому в качестве начального приближения выбрана точка хо = b. Как видно из рисунка, метод имеет очень быструю сходимость среди всех методов решения нелинейных уравнений: обычно заданная точность достигается за 2-3 итерации.
Достоинство метода Ньютона: очень быстрая сходимость по сравнению с методом половинного деления и методом простой итерации к заданной точности. Недостаток: громоздкий алгоритм: на каждой итерации необходимо вычислять значение функции и ее первой производной.
Метод хорд
Для реализации данного метода, нужно построить исходную функцию y=F(x) и найти значения функции на концах отрезка F(a) и F(b). Затем провести хорду М1M2 c концами в точках М1(a, F(a)) и M2(b, F(b)). Абсцисса точки пересечения хорды М1M2 с осью OX это и есть приближенный корень x1. Далее найти точку M3(X1,F(x1)), построить следующую хорду и найти второй приближенный корень x2. И так далее. В зависимости от поведения функции возможны два случая:
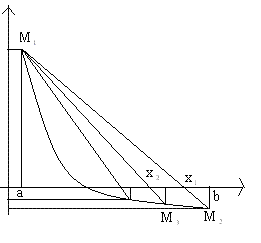 Рис. 1 Рис. 1
| 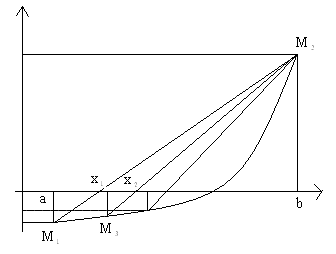 Рис. 2 Рис. 2
|
Для первого случая (Рис. 1) справедлива следующая формула (8):
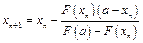
и справедливо неравенство: F(a)*F''(a)>0, где x0=b.
Для второго случая (Рис. 2) справедлива следующая формула (9):
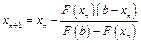
и справедливо неравенство: F(b)*F''(b)>0, где x0=a.
Условия сходимости метода секущих аналогичны условиям сходимости метода Ньютона, т. е.:
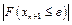
Дата публикования: 2015-11-01; Прочитано: 418 | Нарушение авторского права страницы | Мы поможем в написании вашей работы!
